Non-Linear Ion-Acoustic Solitary Waves in Electron-Positron-Ion Plasma with Non-Thermal Electrons ()
1. Introduction
The electron-positron (e-p) plasmas have frequent occurrence in the Universe [1] . The inclusion of an ion in an e-p forms an e-p-i plasma. These e-p-i plasma are ubiquitious in astronomical environments. In such situations, positrons drastically change the behaviour of non-linear waves and it is for this reason that they have attracted the attention of several authors [2] [3] [4] [5] .
Large amplitude ion-acoustic waves in e-p-i plasma were studied by [2] , using the Sagdeev potential technique. Their results showed that the larger the relative positron density, the lower the Mach number for a soliton of fixed amplitude to propagate. Later, [3] , studied the effect of the ion temperature on large amplitude ion-acoustic waves in e-p-i plasma consisting of Boltzmann distributed posi- trons. He found that the ion temperature increased the maximum Mach number and decreased the amplitude of ion-acoustic waves. Furthermore, in studying non-linear acoustic excitations in e-p-i plasma, [4] studied the accretion disks of active galactic nuclei, where the ion temperatures were much higher than those of electrons and positrons. Due to very high ion temperatures in accretion disks, the ions were modeled using the Boltzmann distribution, whereas the electrons and positrons were governed by the fluid equations. Most research work about e-p-i plasmas have treated electrons as being Boltzmann distributed species thereby, leaving kappa distributed electrons not adequately studied.
The kappa 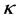 distribution function possesses the desired property that the particles with velocities greater than the thermal velocity obey a power law distribution and gives better fits to real space plasma [6] . The family of isotropic generalised Lorentzian or
distribution function possesses the desired property that the particles with velocities greater than the thermal velocity obey a power law distribution and gives better fits to real space plasma [6] . The family of isotropic generalised Lorentzian or 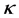 -distributions takes the form [7] :
-distributions takes the form [7] :
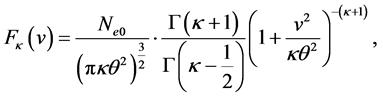 (1)
(1)
where 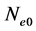 is the unperturbed equilibrium electron density,
is the unperturbed equilibrium electron density, 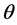 is the most probable speed of the particle species related to the usual thermal velocity,
is the most probable speed of the particle species related to the usual thermal velocity,
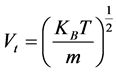 by
by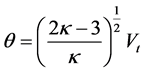 ; T being the characteristic kinetic tempera-
; T being the characteristic kinetic tempera-
ture, i.e., the temperature of equivalent Maxwellian distribution with same average kinetic energy;  is Boltzmann’s constant,
is Boltzmann’s constant, 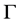 is the usual gamma function, and
is the usual gamma function, and 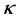 is the spectral index that determines the hardness of the energy spectrum corresponding to the presence of excess suprathermal particles in the tail of the distribution function [8] . In the limiting case, when
is the spectral index that determines the hardness of the energy spectrum corresponding to the presence of excess suprathermal particles in the tail of the distribution function [8] . In the limiting case, when 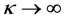 (e.g
(e.g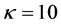 ), the distribution function approaches the familiar Maxwellian form (Figure 1). Low values of
), the distribution function approaches the familiar Maxwellian form (Figure 1). Low values of 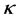 represent distributions with relatively large com- ponent of particles with speeds greater than the thermal speed (“superthermal particles”) and an associated reduction in “thermal” particles, as one observes in a “hard” spectrum [9] .
represent distributions with relatively large com- ponent of particles with speeds greater than the thermal speed (“superthermal particles”) and an associated reduction in “thermal” particles, as one observes in a “hard” spectrum [9] .
Apart from kappa distributed electrons, electron populations can suit other non-thermal distributions eg. Cairn’s distribution [10] . Recently, [5] , used Cairn’s distributed electrons in an e-p-i plasma and [11] applied the distribution on a 4-component complex dusty plasma. In both cases, solitons of both polarities were found to exist. However, for a 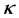 distributed electron population,
distributed electron population,
![]()
Figure 1. Comparision of generalised Lorentzian distribution for the spectral index κ = 2, 5, 10, and κ = ∞ (corresponding to Maxwellian distribution).
solitons of both polarities may not arise. Therefore, this study investigated the effect of using  distributed electrons in an e-p-i plasma.
distributed electrons in an e-p-i plasma.
This paper is therefore structured with the following sections: A brief intro- duction, description of the model, discussion of results and finally we present a conclusion.
2. Description of Plasma Model
We considered a simple three species unmagnetised and collisionless plasma model whose electrons are kappa-distributed. The other species are warm inertial adiabatic fluid ions and Boltzmann-distributed positrons, thereby referred to as an e-p-i plasma. The electrons, positrons, and ions are considered to have temperatures ![]() and
and ![]() respectively. Again, the electrons, ions, and positrons are assumed have densities of
respectively. Again, the electrons, ions, and positrons are assumed have densities of ![]() and
and ![]() respectively.
respectively.
The charge equilibrium equation for the system when electrostatic potential, ![]() is given by
is given by
![]() (2)
(2)
where ![]() is the ratio of equilibrium number density of ions to electrons,
is the ratio of equilibrium number density of ions to electrons, ![]() is the ratio of equilibrium number density of positrons to electrons.
is the ratio of equilibrium number density of positrons to electrons.
Integrating the adopted kappa distribution Equation (1), the velocity space gives the unnormalised electron number density as
![]() (3)
(3)
It can be noted that Equation (3) is only valid for![]() , and kappa distribu-
, and kappa distribu-
tions reduce to Maxiwellian distributions, when ![]() [12] , while for low values of
[12] , while for low values of![]() , “hard” spectrum with strong non-Maxiwellian tail following a power-law at high speeds are obtained [7] . Normalizing by appropriate scaling quantities, the electron number density is obtained in dimensionless form as
, “hard” spectrum with strong non-Maxiwellian tail following a power-law at high speeds are obtained [7] . Normalizing by appropriate scaling quantities, the electron number density is obtained in dimensionless form as
![]() (4)
(4)
where ![]() is particle density and the electrostatic potential
is particle density and the electrostatic potential ![]() are scaled as
are scaled as
![]() and
and![]() .
.
The positrons follow the Boltzmann distribution given as,
![]() (5)
(5)
Normalising with respect to![]() , the number density for positrons may be written in a dimensionless form as
, the number density for positrons may be written in a dimensionless form as
![]() (6)
(6)
where, ![]() ,
, ![]() and
and![]() .
.
For ions, the density is obtained from the fluid equations. These are continuity, pressure, and momentum equations written respectively as follows:
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
where, ![]() and
and ![]() are the un-normalized ion fluid speed and ion thermal pressure respectively;
are the un-normalized ion fluid speed and ion thermal pressure respectively; ![]() is the ion mass (charge), and
is the ion mass (charge), and ![]() is the un-normalized space (time) variable.
is the un-normalized space (time) variable.
This system of Equations (7)-(9) are normalized by introducing dimensionless
quantities (![]() and
and![]() ) such that;
) such that;![]() ;
;![]() ;
;![]() ;
;
![]() ;
; ![]() and
and![]() . Here,
. Here, ![]() is
is
Debye length, ![]() is ion acoustic speed, while
is ion acoustic speed, while ![]() is
is
plasma frequency with ![]() and e the ion mass and electronic charge respectively.
and e the ion mass and electronic charge respectively.
The normalised equations are obtained as:
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
In transforming to the stationary frame, the solution of nonlinear equations of a wave depends on x and t through the variable![]() . Here M is the Mach number (normalized by the phase speed of the ion-acoustic waves). Thus,
. Here M is the Mach number (normalized by the phase speed of the ion-acoustic waves). Thus,
![]() and
and![]() . We can now integrate Equations (10)-(12) applying
. We can now integrate Equations (10)-(12) applying
boundary conditions as![]() ;
; ![]() and
and![]() , and eliminating
, and eliminating ![]() between the three expressions to obtain the ion density equation as,
between the three expressions to obtain the ion density equation as,
![]() (13)
(13)
where ![]() and
and![]() .
.
It is easy to show from Equation (13) that for![]() , the negative sign is used and for
, the negative sign is used and for![]() , the positive is used. The negative sign corre- sponds to supersonic species [13] . The negative sign satisfies the boundary condition of
, the positive is used. The negative sign corre- sponds to supersonic species [13] . The negative sign satisfies the boundary condition of ![]() with
with ![]() as
as![]() . As a result, the ion density is obtained as
. As a result, the ion density is obtained as
![]() (14)
(14)
Equation (4), (6) and (14) are coupled by Poisson’s equation,
![]() (15)
(15)
where ![]() is permittivity of free space and
is permittivity of free space and ![]() (for ions),
(for ions), ![]() (for positrons) and
(for positrons) and ![]() (for electrons). Normalising with
(for electrons). Normalising with![]() , gives
, gives
![]() (16)
(16)
In the stationary frame,
![]() (17)
(17)
Therefore,
![]() (18)
(18)
Substituting Equations (4), (6) and (14) into Equation (16), and integrating with respect to![]() , the usual energy equation [14] is obtained as
, the usual energy equation [14] is obtained as
![]() (19)
(19)
where ![]() represents a potential well with
represents a potential well with ![]() playing the role of “coor- dinate” (pseudoposition) and
playing the role of “coor- dinate” (pseudoposition) and ![]() represents the role of “time”. From Equation (18) and Equation (19) the Sagdeev potential or pseudopotential is obtained as
represents the role of “time”. From Equation (18) and Equation (19) the Sagdeev potential or pseudopotential is obtained as
![]() (20)
(20)
3. Results
3.1. Theoretical Analysis
The derived Sagdeev potential, ![]() is vital in finding the existence domains of IAS waves. For solitary waves to propagate in an e-p-i plasma, Sagdeev potential,
is vital in finding the existence domains of IAS waves. For solitary waves to propagate in an e-p-i plasma, Sagdeev potential, ![]() and its derivatives with respect to
and its derivatives with respect to ![]() must satisfy the following conditions [15] .
must satisfy the following conditions [15] .
1) ![]() at the origin
at the origin![]() .
.
2) ![]() such that the origin is unstable i.e.,
such that the origin is unstable i.e., ![]() has maximum at origin.
has maximum at origin.
3) ![]() and
and ![]() for
for![]() . i.e.,
. i.e., ![]() for positive root (positive potential) and
for positive root (positive potential) and ![]() for negative root (negative potential). The primes represent derivatives of
for negative root (negative potential). The primes represent derivatives of ![]() with respect to
with respect to![]() .
.
Clearly, from Equation (20), ![]() and its derivative with respect to
and its derivative with respect to ![]() vanish at
vanish at ![]() hence condition (1) is satisfied. The origin at
hence condition (1) is satisfied. The origin at ![]() thus defines the equilibrium state, which represents a local maximum of
thus defines the equilibrium state, which represents a local maximum of![]() .
.
The requirement, ![]() yields
yields
![]() (21)
(21)
where ![]() is the lower Mach number limit below which no soliton can exist. For
is the lower Mach number limit below which no soliton can exist. For ![]() Equation (21) becomes
Equation (21) becomes
![]() (22)
(22)
which inequality is part of the soliton (existence) condition to be fulfilled as
![]() (23)
(23)
i.e., using the charge neutrality condition in Equation (2). For the fixed value of![]() , solitons may exist only for values of the Mach number satisfying
, solitons may exist only for values of the Mach number satisfying
![]() (24)
(24)
This is on the basis of investigations by [13] [15] who showed that the existence of solitons required![]() . This implies that solitons can have finite amplitudes at
. This implies that solitons can have finite amplitudes at ![]() in the region where solitons with both polarity exit. For
in the region where solitons with both polarity exit. For![]() ,
, ![]() and
and ![]() Equation (23) reduces to the familiar expression
Equation (23) reduces to the familiar expression
![]() (25)
(25)
It follows that if Equation (24) is the “true” Mach number, the structures would be truly supersonic.
Figure 2(a) shows the necessary minimum Mach number for the existence domains of solitary structures. For the three component plasma, Figure 2(a), shows that there are two acoustic existence ranges for the solitary waves i.e., between![]() , before the thermal velocity and
, before the thermal velocity and ![]() after the thermal velocity. Therefore,
after the thermal velocity. Therefore, ![]() is the minimum Mach number limit below which no solitary waves exist for this current model. For the case of this study, solitons with positive polarity are limited by infinite compression of the inertial ions. This is achieved when
is the minimum Mach number limit below which no solitary waves exist for this current model. For the case of this study, solitons with positive polarity are limited by infinite compression of the inertial ions. This is achieved when
![]() , leading to a sufficient condition,
, leading to a sufficient condition,![]() . After
. After
finding the minimum Mach number, ![]() , for the nonlinear solitary structures, the maximum Mach number,
, for the nonlinear solitary structures, the maximum Mach number, ![]() was found using Equation (14). Another
was found using Equation (14). Another
limiting potential was obtained to be ![]()
Both ![]() and
and ![]() yields a complex
yields a complex![]() . Therefore,
. Therefore, ![]() and
and ![]() are the practical constraints limiting positive potential solitons, under the condition
are the practical constraints limiting positive potential solitons, under the condition ![]() and
and![]() . The critical limiting potential
. The critical limiting potential![]() , since
, since ![]() for all M and f. Therefore, the requirement
for all M and f. Therefore, the requirement
![]() leads to the upper limit on M as
leads to the upper limit on M as ![]() for the existence of positive solitons (see Figure 2(b)). In this case of a three component plasma model, the solution for the existence domains exist in the range
for the existence of positive solitons (see Figure 2(b)). In this case of a three component plasma model, the solution for the existence domains exist in the range
![]() .
.
3.2. Numerical Analysis
Numerical solutions of the existence domains supported by the plasma model
consisting of three species were obtained using the Sagdeev potential in Equation (20).
3.2.1. Existence Diagrams
Figure 3(a) shows the existence domains for solitons in parameter space of maximum and minimum Mach numbers for a plasma with electrons having the
same temperature as positrons, i.e.,![]() . Positive solitons at different
. Positive solitons at different
values of ![]() (i.e.,
(i.e., ![]() are indicated by blue dots,
are indicated by blue dots, ![]() , by red thick line,
, by red thick line,
and ![]() by black dashed line where
by black dashed line where ![]() and
and![]() . It can
. It can
clearly be seen that the existence domains of finite amplitude ion acoustic solitary waves are confined within the limits of Mach number given by Equation (23) and (24), respectively. For the values of ![]() used, the positive potential solitons exist for the full range (
used, the positive potential solitons exist for the full range (![]() ) of the density ratio. For this case, the existence domain increased with increase in
) of the density ratio. For this case, the existence domain increased with increase in![]() .
.
Figure 3(b) shows numbers, M plotted against the electron-positron tempera- ture ratio, ![]() for various values of ion-to-electron temperature ratio (
for various values of ion-to-electron temperature ratio (![]() plotted in blue dots,
plotted in blue dots, ![]() in red thick line, and
in red thick line, and ![]() in black dashes) where
in black dashes) where![]() ,
, ![]() and
and![]() . Finally, it was observed that increasing the electron-positron (e-p) temperature ratio,
. Finally, it was observed that increasing the electron-positron (e-p) temperature ratio, ![]() increased the Mach number of the solitary wave. It is predictable that when temperature ratio,
increased the Mach number of the solitary wave. It is predictable that when temperature ratio, ![]() is increased, a corresponding increase in the existence domains of the finite amplitude ion acoustic solitary waves is obtained. Having discused the existence domains of IAS waves in an e-p-i plasma, the effects of kappa distributed electrons and inertial warm ions on propagation of IAS waves is discussed next.
is increased, a corresponding increase in the existence domains of the finite amplitude ion acoustic solitary waves is obtained. Having discused the existence domains of IAS waves in an e-p-i plasma, the effects of kappa distributed electrons and inertial warm ions on propagation of IAS waves is discussed next.
3.2.2. Effect of Kappa Distributed Electrons
Figure 4(a) shows the variation of the Sagdeev potential, ![]() with
with ![]() for a fixed Mach number,
for a fixed Mach number, ![]() , and various values of
, and various values of ![]() ranging from 3 (in purple dots) to 10 (red thick line). Different values of
ranging from 3 (in purple dots) to 10 (red thick line). Different values of ![]() were used to examine the one that would give a better fit to the kappa distribution. It is clearly observed that for a lower value of
were used to examine the one that would give a better fit to the kappa distribution. It is clearly observed that for a lower value of![]() , the amplitude of the solitary electrostatic potential structures increased from 0.04 for
, the amplitude of the solitary electrostatic potential structures increased from 0.04 for![]() , to 0.10 for
, to 0.10 for![]() . Hence, for a fixed M, a decrease in
. Hence, for a fixed M, a decrease in ![]() causes an increase in the true sound speed. Thus, it follows that a decrease in
causes an increase in the true sound speed. Thus, it follows that a decrease in ![]() leads to larger solitons, as shown in Figure 4(a). Furthermore, the depth of the Sagdeev potential increased from 0.0001 to 0.0015 over the range (
leads to larger solitons, as shown in Figure 4(a). Furthermore, the depth of the Sagdeev potential increased from 0.0001 to 0.0015 over the range (![]() ). Thus, the soliton profile increased as the non- thermal component was increased. When the amplitude increased, it resulted into the soliton profile, which become a bit steeper. Figure 4(b) is a plot of
). Thus, the soliton profile increased as the non- thermal component was increased. When the amplitude increased, it resulted into the soliton profile, which become a bit steeper. Figure 4(b) is a plot of ![]() against
against ![]() showing the bell shaped electrostatic potential. It is clearly seen that for lower values of
showing the bell shaped electrostatic potential. It is clearly seen that for lower values of![]() , say
, say![]() , the potential amplitude increased as the width decreased, while for high values (
, the potential amplitude increased as the width decreased, while for high values (![]() ), the potential amplitude decreased as the width of the solitary structures increased.
), the potential amplitude decreased as the width of the solitary structures increased.
3.2.3. Effect of Inertial Warm Ions
Figure 5(a) showed the variation of Sagdeev potential, ![]() with
with ![]() for a fixed M (0.60),
for a fixed M (0.60), ![]() , and various values of
, and various values of![]() , ranging from
, ranging from ![]() (thick) to
(thick) to ![]() (black thick line) of solitary electrostatics potential structure. When the different values of ion-to-electron temperature rations,
(black thick line) of solitary electrostatics potential structure. When the different values of ion-to-electron temperature rations, ![]() were reduced from 0.025 to 0.015 and the potential increased from 0.0378 to 0.06436, particle trapping was exhibited, which implied the formation of solitons. Thus, for fixed M and
were reduced from 0.025 to 0.015 and the potential increased from 0.0378 to 0.06436, particle trapping was exhibited, which implied the formation of solitons. Thus, for fixed M and![]() , a decrease in
, a decrease in ![]() resulted into high amplitude solitons. Again, Figure 5(a) showed that the depth of Sagdeev potential increased from 0.00005786 to 0.000265. This implied that solitons exists with potential wells of
resulted into high amplitude solitons. Again, Figure 5(a) showed that the depth of Sagdeev potential increased from 0.00005786 to 0.000265. This implied that solitons exists with potential wells of ![]() profiles at different depths. In non-thermal
profiles at different depths. In non-thermal
![]()
![]() (a) (b)
(a) (b)
Figure 4. (a) Variation of ![]() against
against ![]() for
for![]() ,
, ![]() ,
, ![]() ,
, ![]() and various values of kappa:
and various values of kappa: ![]() (purple dots),
(purple dots), ![]() (green dashes),
(green dashes), ![]() (black dots),
(black dots), ![]() (red thick line). (b) Arbitrary amplitude ion acoustic pulses,
(red thick line). (b) Arbitrary amplitude ion acoustic pulses, ![]() against
against ![]() for different values of
for different values of![]() :
:![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() (black thick line),
(black thick line), ![]() (blue dots), and
(blue dots), and ![]() (green thick line).
(green thick line).
![]()
![]() (a) (b)
(a) (b)
Figure 5. (a) Variation of ![]() against
against ![]() for
for![]() ,
, ![]() ,
, ![]() ,
, ![]() and various values of
and various values of![]() :
: ![]() (red thick curve),
(red thick curve), ![]() (green dotted curve), and
(green dotted curve), and ![]() (black thick curve). (b) Arbitrary amplitude of ion acoustic pulses,
(black thick curve). (b) Arbitrary amplitude of ion acoustic pulses, ![]() against
against ![]() for various values of ion-to-electron temperature ratio
for various values of ion-to-electron temperature ratio![]() :
:![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() (red thick line),
(red thick line), ![]() (green dots), and
(green dots), and ![]() (black thick line).
(black thick line).
environment, plasma formation is more likely and amplitude of the soliton is maximum because of greater depth.
In Figure 5(b), the electrostatic potential, ![]() is plotted against
is plotted against![]() , for varying
, for varying ![]() values. Only bell shaped electrostatic potentials are obtained. The potential amplitude increased as ion-to-electron temperature ratio,
values. Only bell shaped electrostatic potentials are obtained. The potential amplitude increased as ion-to-electron temperature ratio, ![]() decreased. However, the width of the solitary structures increased with increasing ion-to- electron temperature ratio,
decreased. However, the width of the solitary structures increased with increasing ion-to- electron temperature ratio,![]() . Furthermore, it is shown that the potential amplitude
. Furthermore, it is shown that the potential amplitude![]() , in the non-thermal case was higher for smaller value of
, in the non-thermal case was higher for smaller value of![]() , but this trend became weaker for bigger values, say
, but this trend became weaker for bigger values, say![]() . It was noted that the effect of
. It was noted that the effect of ![]() on the amplitude of the solitary waves was weaker for non-thermal case when
on the amplitude of the solitary waves was weaker for non-thermal case when ![]() as shown by the black thick curve and green dotted curve in Figure 5(b). In conclusion, the effects of ion temperature ratio
as shown by the black thick curve and green dotted curve in Figure 5(b). In conclusion, the effects of ion temperature ratio ![]() on the properties of the new solitary wave are more pronounced for smaller
on the properties of the new solitary wave are more pronounced for smaller![]() .
.
4. Conclusion
The study findings show a fully non-linear ion acoustic solitary wave in e-p-i plasma with three species (i.e., warm inertial adiabatic ion fluid, kappa- distributed electrons, and Boltzmann-distributed positrons). The existence of large amplitude ion acoustic solitons of positive electrostatic potential was obtained. Numerical solution of the energy integral equation showed that positive solitary waves existed with a property of having faster pulses with taller and slender amplitudes. Furthermore, increasing the non-thermal parameter![]() , it was found that the amplitudes of ion acoustic solitons were reduced when a significant fraction of positrons is present in the plasma. This implied that the positron component hindered the propagation speed of the solitons. These results are capable of enhancing the understanding of non-linear structures in e-p-i plasmas found in certain astronomical environments containing non- thermal electrons as a component.
, it was found that the amplitudes of ion acoustic solitons were reduced when a significant fraction of positrons is present in the plasma. This implied that the positron component hindered the propagation speed of the solitons. These results are capable of enhancing the understanding of non-linear structures in e-p-i plasmas found in certain astronomical environments containing non- thermal electrons as a component.
Acknowledgements
We acknowledge the funding from East African Astronomical Research Network (EAARN) and support from the International Science Program (ISP) based in Uppsala University in Sweden.