Dynamic Response Analysis of High-Speed Train Gearbox Housing Based on Equivalent Acceleration Amplitude Method ()
1. Introduction
Due to its high speed, large transport capacity, low energy consumption, light pollution, less land occupation, high safety performance and other technical and economic advantages, the high-speed rail has attracted universal attention from countries all over the world. However, with the increasing train speed, the vibration of components of the train also increases significantly. Vibration not only affects passengers’ comfort, but poses great potential risks to the normal operation of a train, in particular to the drive system of high-speed train. Gearbox, as one of the crucial transmission equipment of high-speed train drive system, often operates under high speed and heavy load, and the fatigue property of its structure directly affects the safety of the train in its operation [1] . Since the year of 2012, accumulatively over 100 failures of gearbox have occurred with high- speed train in China presenting as fatigue crack on the gearbox housing. Therefore, the study of vibration characteristics of high-speed train gearbox is of great engineering significance for ensuring normal operation of a train and the design of the new housing of the gearbox.
Normally, high-speed train gearbox is installed with one end hanged on the axle through the bearing and the other end connected with bogie frame through the suspension device [2] . Gearbox housing is the supporting body of the train drive system. When a train is moving, it must bear the wheel-rail excitation from the load end due to the irregularity of wheel/rail and the inherent harmonic torque from the asynchronous motor. Also, because of the periodic variation of the meshing stiffness during the gear meshing process, the vibration caused by the internal dynamic excitation will transfer to the housing through transmission shaft and via bearing. Researchers have done a lot of studies on the dynamic performance of gearbox [3] [4] [5] . However, these researchers mainly have focused on the traditional mechanical field, while there are not many studies on vibration of high-speed train gearbox. Apart from sustaining the traditional mechanical vibration, high-speed train gearbox also bears powerful wheel/rail impact. Reference [6] involves an in-depth exploration of the vibration characteristics and the frequency distribution of high-speed train, based on test data collected on the Wuhan-Guangzhou Railway, which shows that the main vibration frequency of the wheel-rail excitation is within 400 - 600 Hz. Reference [7] involves a simulation analysis where dynamic responses of the gearbox housing of high-speed train under internal and external excitation are studied, and frequency of the harmonic torque of the asynchronous motor and the gear-mesh frequency are considered, with the vibration characteristics of the gearbox housing under wheel-rail excitation remaining to be further investigated. Due to the differences of the lines and the vehicles, there is no specific stipulation of the wheel/rail vibration loads to be borne by the gearbox housing in various countries. Traditionally, fatigue strength assessment is largely based on the single external load [8] , making it hard to reflect the housing invalidation problem caused by the action of the dynamic load when a train is moving at high speed.
In this paper, the vibration characteristics of the gearbox housing under the excitation of wheel-rail interaction are analyzed based on the measured data of Wuhan-Guanzhou high speed rail. Spectrum analysis of the vibration responses is performed by applying the data processing software independently developed by the structural strength testing laboratory of Beijing Jiaotong University, based on the vibration response signals of the high-speed period which is selected randomly and the analysis of its frequency characteristics, the vibration relationship among different parts of gearbox housing is explored by defining the equivalent acceleration amplitude, and analysis and validation are carried out based on the line data.
2. Random Vibration Equation and Wheel-Rail Excitation
According to the mechanic vibration theory [9] , the mathematical differential equation of the motivated mechanical system is
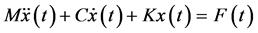(1)
where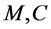 
and 
are the system’s mass matrix, damping matrix and stiffness matrix respectively;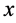 
is the system response; 
is the excitation imposed on the system.
Since the parameters of a complex structure such as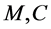 
and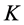 
are hard to be obtained, its mechanical vibrating system is usually represented by the input-output system as
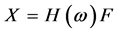(2)
where X and F are the response and the excitation of the system in frequency domain,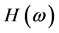 
is the function with frequency 
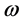as its independent variable, and can be obtained through the frequency scanning test or the finite element harmonic response analysis.
3. Measuring Point Layout and the Numerical Treatment
3.1. Test Sensor Layout
Gearbox, as the critical component of the high-speed train responsible for the driving torque and moving the train forward, its vibration load mainly comes from the wheel-rail excitation in its application. In order to understand the characteristics of the vibration load borne by the gearbox housing when the high-speed train is running, a line test was performed on the Wuhan-Guangzhou High-speed Rail (with a total length of 1070 kilometers), with the tested gearbox located at the first car of the train. The axle box and the gearbox are installed with several three-dimensional acceleration sensors, so that the vertical, the horizontal and the longitudinal vibrations can be tested at each measuring point. In this paper, the acceleration measuring points are shown in the Figure 1. The measuring point A is situated at the joint of the gearbox housing and the axle bearing block, where the vibration response is viewed as input signal of the wheel-rail excitation received by the gearbox housing. Measuring point B is situated at the upper part of the gearbox housing, where the vibration response is
![]()
Figure 1. Layout of Measuring Points of Gearbox housing.
viewed as output signal of the wheel-rail excitation received by the gearbox housing.
3.2. Numerical Treatment Method
The data of the actual line test must first undergo the numerical treatment, and then the effective information of the signal and the vibration characteristics of the gearbox housing can be obtained. Therefore, the acceleration-time history of the test position is obtained after the tested signals are cleared zero drift and are treated with excrescent interference. Time-domain signals under main working conditions are processed with Fourier transform, so as to acquire the corresponding frequency distribution and the power spectral density, etc. The Fourier transform expression of discrete-time signal is shown as Formula 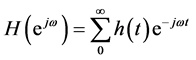(3).
(3)
where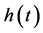 
is the auto-correlation function of test signal.
After the aforementioned transformation, the real part (Re) and imaginary part (Im) corresponding to the transformed data and the length of the input sequence n can be obtained, and the nominal mean square amplitude defined here can be expressed as
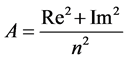(4)
Formula (4) refers to the spectral density value of the vibration acceleration within unit frequency in its physical implication, which indicates the main frequency components of input signals and its weighted density, and also shows the degree that the signal offsets the central position at a certain frequency or within a period. For vibration signal, it shows the energy density and intensity of vibration corresponding to the frequency, while peak value and amplitude value of the vibration acceleration signal reflects to some extent vibration intensity of the vehicle system.
4. Response Analysis of Gearbox Housing Vibration
Since the high-speed train usually runs at high speed, the motion characteristics under this state can represent the main vibration behavior and the characteristics of vehicle system. Therefore, in this paper the analysis of the train under operation at high speed was performed. Actual line test involves many complete round-trip journey of the application, with long mileage, full range of running conditions and large data. Since it is impossible to list all the testing data, sampling analysis of the line testing data is adopted in this paper.
4.1. Analysis of Vibration of Different Parts of Gearbox Housing
Figure 2 shows the time history and the frequency spectrum of the vibration response signal at measuring point A, with horizontal maximum acceleration arriving at 23.6 g, main vibrating frequency ranging from 560 - 585 Hz, and the points with higher energy existing at the frequency of 150 Hz; it also shows vertical maximum acceleration of 20.1 g, and a distribution of main vibrating frequency ranging from 560 - 585 Hz.
Figure 3 shows the vibration response signal at measuring point B, with the maximum horizontal acceleration of 19.7 g and the maximum vertical acceleration of 16.0 g; frequency analysis shows that main vibrating frequency is distributed in frequency band of 560 - 585 Hz, while points with higher energy also exist where the frequency reaches 150 Hz.
Both Figure 2 and Figure 3 show that the maximum value of the vibration acceleration at measuring point A is higher than that at measuring point B, indicating a decline of vibration of housing structure as it is farther away from the axle. As for the vibration frequency, main vibrating frequencies all fall in the frequency band of 560 - 585 Hz, with the most intense vibration of the gearbox housing to be found at 575 Hz, and the second highest energy point to be found at about 150 Hz in the housing of horizontal vibration.
In order to analyze the vibration of different parts of gearbox, in this paper, the data processing and the fatigue strength evaluation system independently developed by Beijing Jiaotong University is applied to process the test data collected on the Wuhan-Guangzhou Railway. One-dimensional acceleration spectrum is prepared after a series of steps including getting the time course of the acceleration vibration response, processing the abnormal signal, filtering the band pass, selecting the peak-valley value, and counting the acceleration amplitude by adopting the rain-flow counting method. Figure 4 shows the acceleration amplitude spectrum curve corresponding to different measuring points of gearbox housing.
![]()
(a)![]()
(b)
Figure 2. Acceleration Vibration Signal at Measuring Point A. (a) Acceleration Time Course (b) Acceleration Spectrum.
Figure 4 shows that within a certain amplitude range horizontal acceleration is higher than vertical acceleration at the same measuring point; for different measuring points, vibration acceleration at measuring point A is higher than that at measuring point B, showing that the vibration wave experiences an attenuation during transmission. In order to explore the vibration intensity of different parts of gearbox housing, a definition of the equivalent acceleration am-
![]()
(a)![]()
(b)
Figure 3. Acceleration Vibration Signal at Measuring Point B. (a) Acceleration Time Course (b) Acceleration Spectrum.
plitude is given as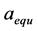
, and the calculation formula is
![]()
(5)
In the formula, ![]()
is the corresponding number of ![]()
amplitudes of acceleration spectrum at each level. Based on Formula (5), vibration of different parts of gearbox housing can be obtained as shown in Table 1.
Table 1 shows that both the horizontal and vertical equivalent acceleration amplitudes at measuring point A are higher than that at measuring point B, indicating that there exists attenuation during transmission.
![]()
Figure 4. Acceleration Amplitude Spectrum.
![]()
Table 1. Equivalent Acceleration Amplitude at Different Measuring Points/g.
4.2. Identify the Headings
China’s high-speed train mainly consists of 8 carriages. When the high-speed train is running, it is defined as positive driving if carriage 1 is the tail of the train, and reverses driving if carriage 8 is the head of the train. Figure 5 shows the acceleration-time history of the gearbox housing corresponding to the high- speed train in positive driving and reverse driving respectively. Figure 5 shows that the horizontal vibration acceleration of the gearbox in the test in the housing of reverse driving is notably higher than that in the housing of positive driving.
Acceleration time course as shown in Figure 5 is processed with mathematical statistics using the rain-flow counting method, and acceleration amplitude spectrum is prepared as shown in Figure 6. According to the figures, horizontal vibration is notably higher than vertical vibration in the high acceleration amplitude area. Comparison of positive driving and reverse driving shows that when horizontal acceleration is higher than 25 g, the frequency of large amplitude response of train in its positive driving is higher than that in reverse driving; the vertical acceleration amplitude of the gearbox in positive driving is lower than that in reverse driving across the whole section.
Formula (5) is used to calculate equivalent acceleration amplitude, as shown in Table 2. According to Table 2, when a train changes from positive driving to
![]()
(a)![]()
(b)
Figure 5. Acceleration Time Course of Gearbox housing. (a) Positive Driving of Train (b) Reverse Driving of Train.
![]()
Table 2. Gearbox Vibration Response in Different Driving Directions/g.
reverse driving, the equivalent acceleration amplitude of gearbox’s horizontal vibration increases from 3.6 g to 5.8 g, an increase of 61%; the equivalent accele-
![]()
Figure 6. Acceleration Amplitude Spectrum
![]()
(a)![]()
(b)
Figure 7. Acceleration Time Course of Gearbox housing. (a) Speed at 200 km/h; (b) Speed at 300 km/h.
ration amplitude of gearbox’s vertical vibration increases from 4.3 g to 4.8 g, an increase of 12%. There are over 200 tunnels along the Wuhan-Guangzhou Railway. According to the dynamic test, the head carriage is more stable than the tail one when the high-speed train is running. As a result, vibration level of the gearbox of carriage 1 under test is higher in positive driving than that in reverse driving.
4.3. Impact of the Running Speed of the Train on the Vibration of Gearbox Housing
In order to explore the impact of train’s running speed on the vibration of gearbox housing, acceleration time curves of gearbox housing corresponding to the train running at 200 km/h and 300 km/h are shown in Figure 7, selected according to the GPS signals. According to the Figure, maximum horizontal and vertical accelerations of gearbox housing are 23.1 g and 16.8 g respectively when a high-speed train is running at 200 km/h; and 28.1 g and 25.9 g at 300 km/h, showing that the gearbox vibration level rises as the high-speed train speed increases.
Acceleration time course as shown in Figure 7 is processed with the rain-flow counting method, and the acceleration amplitude spectrum is prepared as shown in Figure 8. The acceleration spectrum shows that vibration amplitude of gearbox is obviously higher when the train runs at high speed than at low speed. The equivalent acceleration amplitudes of gearbox corresponding to different speeds at which high-speed train runs are calculated using Formula (5), and the results are shown in Table 3.
5. Vibration Transfer Analysis
In order to establish the vibration transfer relationship between measuring point A and measuring point B, a definition of equivalent vibration transfer coefficient is given as![]()
, and the formula is
![]()
Figure 8. Acceleration Amplitude Spectrum.
![]()
(6)
In the formula, ![]()
and ![]()
are the equivalent acceleration amplitudes of measuring point A and B respectively, and based on formula, vibration transfer coefficient between the two measuring points of the high-speed gearbox housing can be obtained, as shown in Table 4
In order to verify the efficiency and applicability of Formula (6), two groups of acceleration data of gearbox are drawn at random for analysis. Based on the conclusion of the analysis of main frequency as shown in Figure 2 and Figure 3, bandpass filtering is performed on data with vibration signal of 575Hz being extracted. Acceleration time course after the processing is shown in Figure 9.
Figure 9 shows that vibration response at point A is notably higher than that at point B, and the phase of point A is ahead of that of the point B. Extremums corresponding to measuring point A and B accessed randomly from the data through numerical calculation software MATLAB, and then the extremums at points with larger vibration response are selected, and the transfer coefficient is calculated using the following Formula (7),
![]()
(7)
In the formula, ![]()
is the maximum acceleration at measuring point A, ![]()
is the maximum acceleration corresponding to ![]()
at measuring point B.
Figure 10 and Figure 11 show the discrete graphs of vibration transfer coefficient and vertical vibration transfer coefficient at measuring point A and B of the gearbox housing respectively. According to the graphs, horizontal vibration transfer coefficients are mainly distributed between 0.75 - 0.9, with a relatively denser distribution at about 0.8; while for vertical vibration transfer coefficients, they are mainly distributed between 0.65 - 0.9, with a denser distribution between 0.7 - 0.85. The above results verify that the equivalent vibration transfer coefficient calculated by Formula (6) is reasonable and applicable, so the method can be applied to analyze the vibration response relations at different positions in the practical engineering application. The reason that vibration transfer coefficients are distributed in a scattered way may be the differences of the dynamic
![]()
Table 3. Gearbox Vibration Response in Different Driving Speeds/g.
![]()
Table 4. Transfer Coefficient between Two Measuring Points.
![]()
(a)![]()
(b)
Figure 9. Vibration Acceleration Time Course of Gearbox housing. (a) Horizontal Acceleration Time Course; (b) Vertical Acceleration Time Course.
magnification factors of wheel-rail excitation at different vibration frequencies to the vibration response of gearbox housing.
6. Conclusions
As the crucial component of the drive system of high-speed train, the gearbox takes the impact of the wheel-rail excitation when the train is running at high speed. In this paper, analysis and studies are performed with the vibration characteristics of gearbox housing by testing vibration acceleration signal on the railway.
1) This paper defined the equivalent acceleration amplitude and the equivalent vibration transfer coefficient, and these parameters can be used for analyzing the vibration characteristics of the gearbox of high-speed train fast and effectively.
2) By performing line test, maximum acceleration and main vibrating frequency at different measuring points of the gearbox when the high-speed train was running along the Wuhan-Guangzhou Railway were obtained.
3) By using the gearbox vibration level represented by the equivalent accele-ration amplitude, it was found that both the horizontal and vertical average accelerations at measuring point A were higher than that at point B, showing that there is attenuation during the transmission of gearbox vibration from axle to the upper part of gearbox housing, with the horizontal and vertical vibration levels dropping by 21% and 23% respectively.
4) When the high-speed train changes from positive driving to reverse driv- ing, the equivalent acceleration amplitude of gearbox’s horizontal vibration in-
![]()
Figure 10. Horizontal Vibration Transfer Coefficient Scatter Diagram.
![]()
Figure 11. Vertical Vibration Transfer Coefficient Scatter Diagram.
creased from 3.6 g to 5.8 g, an increase of 61%; the equivalent acceleration amplitude of gearbox’s vertical vibration increased from 4.3 g to 4.8 g, an increase of 12%, showing that the vibration of gearbox in the head car is better than that in the tail car when the train was running at high speed.
5) Horizontal equivalent acceleration amplitude declined from 5.0 g to 2.6 g when high-speed train slowed down from 300 km/h to 200 km/h, a decrease of 48%; and vertical equivalent acceleration amplitude dropped from 3.8 g to 1.8 g, a decline of 53%, showing that the gearbox’s vibration level declines as the train slows down. Therefore, it can prolong the service life of the gearbox adopting slowdown operation scheme without replacing the gearbox.
6) By using the equivalent vibration transfer coefficient as representation of transfer relations at different measuring points, and through analysis of acceleration time curves selected randomly, it was found out that the transfer coefficient of gearbox’s horizontal vibration was 0.79, while the vertical one was 0.77.
Acknowledgements
The work was supported by “The National Key Research and Development Program of China (2016YFB1200403)”. The author would like to thank Professor Liu Zhiming for instruction and thank colleagues at the structural strength testing laboratory of Beijing Jiaotong University for support and advice during this research.