Effect of Tides on the Stratigraphic Resistance of the South Coast of the Laizhou Bay ()
1. Introduction
On a global scale, the economy in coastal regions is booming; therefore, the water consumption is increasing. The overexploitation of groundwater in these areas is common. A hydraulic connection exists between the groundwater and seawater; therefore, the balance between the groundwater and seawater in coastal regions would be destroyed because of natural factors and overexploitation [1] . The seawater will shift to the landward direction along the aquifer influx, and the freshwater resources would be destroyed. The seawater intrusion is widespread in coastal regions globally, particularly in the dryland and semidryland areas. So far, seawater intrusion has been found in dozens of countries and regions such as America, Australia, Lebanon, Israel, Japan, and Egypt [2] .
With increasing exploitation of fresh groundwater resources and sea-level rise due to the global climate change, seawater intrusion has become increasingly severe. Studies on seawater intrusion have been carried out since the late 19th Century. However, most of the studies are based on the assumption of a static sea level, without considering the effect of tidal waves [2] .
In fact, tidal fluctuation is an important driving force for the groundwater flow in coastal areas. Several studies on the effect of tidal fluctuations on ground- water have been conducted since the 1950s [3] . However, the aquifer was assumed to be homogeneous in most of these studies. By studying the variable- density groundwater model, Ataie-Ashtiani et al. believed that tidal fluctuations increased seawater intrusion, thus increasing the thickness of brackish water interface and changing its structure completely [4] . Since then, many scholars have reached the same conclusion as Ataie-Ashtiani’s. They also believed that the effect of tidal action on brackish water interface is small, and the geomorphology and stratigraphic features of sea beach are also important factors in affecting the coastal groundwater [5] [6] [7] [8] . However, all the studies were based on mathematical analysis and numerical simulations. Moreover, strict constraints were set for the theoretical models, or the tidal fluctuations and stratigraphic conditions were processed in simplified ways.
Seawater intrusion has been investigated using hydrographic survey, environmental isotopes, and geophysical methods [2] . Many studies analyzed the relationship between groundwater and tidal effects from the observed groundwater level and conductivity data, and the same conclusions were drawn as those of the numerical analysis [9] [10] [11] . Environmental isotope is a sensitive parameter for seawater intrusion [12] [13] ; however, the environmental isotope method needs higher investment and involves technical complexity. The hydrographic survey method requires installing hydrological monitoring wells and preferably specialized drilling. Compared to the other two methods, the geophysical method is more convenient and economical. Swartz first applied the resistivity method for studying the interface of Hawaii brackish seawater intrusion, and this method was used by many other researchers later [14] [15] [16] . The initial one-dimensional (1D) measurement was developed to two-dimensional (2D) and three-dimensional (3D) measurements gradually [17] . Day-Lewis et al. and Henderson et al. believed that tidal fluctuation affected the resolution and depth range of resistivity tomography [18] [19] . Poulsen et al. and Franco et al. analyzed the seasonal changes in the formation resistivity of the coastal regions in Denmark and Italy, respectively [16] [20] . They believed that the formation resistivity was associated with changing environmental factors including the tidal effects. So far, the resistivity method has been mainly applied in the regional and seasonal studies of seawater intrusion [2] .
In this study, a case of seawater intrusion in the southern coastal plain of Laizhou Bay, Shandong, China was investigated. The mechanism of seawater intrusion, numerical analysis of underground water, structure of brine, and prevention of seawater intrusion in this region were mainly studied [21] . The effect of tidal fluctuation on seawater intrusion has not been reported. The high-den- sity resistivity method was applied to the high-frequency continuous measurement of formation resistivity, followed by the panel data analysis method, which is commonly used in economics. This method was also introduced to study the effect of tidal fluctuation on seawater intrusion in this region. The purpose of the paper is to find a more convenient and economical method about the effect of tides on the seawater intrusion.
2. Geological Settings
The south bank of the Laizhou Bay coastal area (Figure 1) has a warm temperate continental monsoon climate. It has the characteristics of maritime climate because of its location near the sea. Rainfall infiltration is the main groundwater replenishment in this area. The Weibei Plain, which is a typical silty coast in
![]()
Figure 1. Map showing the location of the study area and survey line.
China, was formed by the alluviation of the rivers in the mountainous region in the central part of Shandong province. The terrain in this area is flat and slightly inclined to the north, with an altitude of 2 - 7 m. Alluvial and proluvial plains are present in the south and north, respectively. The quaternary sediments are mainly piedmont alluvial and coastal sediments, with an aggregate thickness of 500 m. Since the late Pleistocene epoch, the area was long in the process of settlement activities. Zhang et al. divided the marine and continental strata in the late Pleistocene and Holocene epochs, identified three times seawater intrusion, and found that the multilevel underground brine was formed during seawater intrusion and regression [22] . The underground brine mostly occurred in the loose sediments in the stratum of the Quaternary marine, which is mainly composed of silt, mingling with fine sand, muddy silt, coarse sand, and silty clay. The aquifer is formed with silt, fine sand, and clay silt. In the range of the Sha River in Laizhou and the Xiaoqing River in Shouguang, the area of subsurface brine is 1500 km2, with a general mineralization degree of 50 - 150 g/L (the highest mineralization degree is up to 217 g/L). The general burial depth is 0 - 60 m, and the value reaches to 70 - 80 m in some area. There are 3 - 4 brine layers including diving underground brine and confined underground brine areas [23] . The diving underground brine occurred in the sandy silt soil in the Holocene marine layer, with an embedded depth of 0 - 15 m. The diving underground brine is attached to the seawater, and the mineralization degree is relatively low [24] .
The Changyi marine special reserve is located in the north of Changyi City, Shandong Province, with a total area of 29.29 km2. The wetland ecological system including tamarix chinensis and marine organisms are protected in this area. Compared to the other regions in the south bank of Laizhou Bay, the primitive natural environment in the Changyi marine special reserve are preserved relatively completely because the effect of human activities is relatively small. Considering that the effect of tidal wave on coastal groundwater is very weak, the effect of human activity was excluded in the earlier study. Human activity will be taken into account in the follow-up study.
3. Equipment and Field Methods
A high-density resistivity method profile with a length of 94 m was configured in the Changyi Marine Ecology Specially Protected Areas on December 13, 2013. The equipment used was Geopen E60dn from Jiaopeng Co. China, using the Werner method. There are 48 electrodes in total, with an electrode spacing of 2 m (Figure 1). Starting at 15:00, 119 measurements were carried out, lasting for 44 h 26 min. The time spacing between two measurements was 23 min. There are 360 data points in each measurement and 42,840 points in total. Because the original measurement data were in the form of inverted triangle, most of them were surface data, and the data points gradually reduced underground. Because mostly the surface data were affected and the underground data were rarely affected, the data of levels 2 to 10 were analyzed, corresponding to an electrode spacing of 4 - 20 m.
The tidal data were obtained from the tidal level information provided by the Weifang City Marine Environment Monitoring Station. The data were measured one time per hour. An interpolation method was applied to match the tidal data with those of the high-density resistivity method [25] (Figure 2).
4. Methodology
The term “panel data” refers to the multivariate time series data, which were obtained by observing the sectional individual in different times continuously. The time series and cross-section data can be used simultaneously during the parameter analysis of the model. This technique is usually applied to the analysis of economic data [26] [27] [28] . Compared to the cross-section and time series data, panel data have many advantages. They provide a large number of data points for researchers, increase the freedom of data, and reduce the explanatory variables of linear degree, thus improving the effectiveness of measurement model estimation. With the improvement of the panel data theory, it has been used to study environmental problems [29] [30] . In this case, the formation resistivity data, which were measured by the high-density resistivity method, were combined with the panel data. The measurement points, which were selected from the section data, can be viewed as 170 cross sections, and 119 measurements can be regarded as the time series data. Therefore, the panel data theory was used to analyze the data.
The main purpose of this case is to investigate the effect of tide on the formation resistivity in different positions. First, the panel data model was selected. Both the section and time were included in the panel data, and the linear data equation, which is often used to analyze the effects of quantitative and qualitative factors, can be expressed as follows [31] :
![]()
Figure 2. Tidal data and interpolation results.
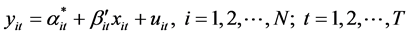 (1)
(1)
where yit is the dependent variable; xit is the k-vector of regression coefficients; 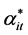 and
and  are the 1 × 1 and 1 × K exogenous variable vectors, which are changed with i and t; i is the cross-section dimension, N is the total number of cross sections; t is the time series dimension; T is the total number of times; uit is the random disturbance term, which is independent of each other and also satisfies zero mean and heteroscedasticity.
are the 1 × 1 and 1 × K exogenous variable vectors, which are changed with i and t; i is the cross-section dimension, N is the total number of cross sections; t is the time series dimension; T is the total number of times; uit is the random disturbance term, which is independent of each other and also satisfies zero mean and heteroscedasticity.
Equation (1) is only used in the description of some cases theoretically. It neither can be estimated nor can be used to predict. Therefore, before the deduction, a structural constraint should be added to the model. First, we assumed that the parameters do not vary with time, but with the individual variation. Therefore, the regression equations for each of the individual components can be defined as follows:
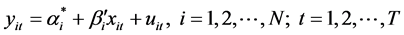 (2)
(2)
There are three types of constraint condition for Equation (2) as follows:
1) The regression slope coefficient is the same; however, the intercept is different, namely, individual-mean corrected regression equation:
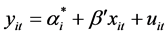 (3)
(3)
2) The regression intercept is the same; however, the slope coefficient is different, namely, unrestricted equation:
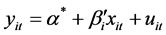 (4)
(4)
3) Both the regression slope coefficient and intercept are the same, namely, pooled regression equation:
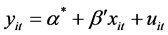 (5)
(5)
In this case, the formation resistivity may be obtained by the panel model regression of the observed value of the tidal level. According to the previous study, the effect of tidal fluctuation on the groundwater at different positions varies, leading to different effects on the formation resistivity; the main performance is that the coefficient changes with the cross section. When each of the measuring point of the formation resistivity was treated as a cross section, the 119 measurements were treated as a time series, and the constraint condition (b) was selected. The expectation equation can be expressed as follows:
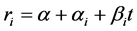 (6)
(6)
where, ri is the formation resistivity for measuring point i; α is a constant; αi is the intercept for measuring point i; βi is the slope coefficient for measuring point i; and t is the tide level for measuring point i at some point.
Because there are only two variable quantities, which are the formation resistivity and tidal level, and the formation resistivity is a function of both time and section, while the tidal level only changes with time, the data do not fully meet the requirements of panel data. Therefore, in the foundation of the conventional model verification method of panel data, the relative error r' was used to validate the calculation results as follows:
 (7)
(7)
where ri is the value calculated by Equation (6) for measuring point i, and xi is the measured value for the same point.
5. Results and Discussion
A variable coefficient model was applied, and the coefficients in model (6) were calculated using the soft of Eveiws 6.0. The model test results are shown in Table 1. The R-squared of the model reaches 0.998794, indicating that the fitness of the model is significant. Because the data applied in this case did not meet the requirements of the panel data totally, Equation (7) was utilized to verify the calculation results. In Equation (6), for each measurement data point, because α and αi were both constants, the effect of tidal change on formation resistivity was only associated to β. If the tidal level changes one unit, the formation resistivity changes β units. Therefore, β was regarded as the influencing strength of tidal change on formation resistivity.
Using the panel data calculation, the β value of each point was obtained, as shown in Figure 3(a). Along the direction of seawater intrusion, the value of β first changed from a negative value to zero and then to a positive value gradually. The value first decreased and then increased. According to Equation (7), statistical analysis was carried out on the error of the results, and the average error is shown in Figure 3(b). When the electrode spacing was <10 m, the error of the panel data calculation was smaller. This indicates that the tidal level mainly affects the surface formation resistivity, instead of deeper formation resistivity. If the error rate is <15% in accordance with the criteria, the distribution of β is shown in Figure 3(c), whose overall trend was consistent with the results shown in Figure 3(a). Supposing the data points, whose errors were >15%, would not affect the formation resistivity, the β value of such points can be regarded as zero. Then, the distribution is shown in Figure 3(d), which was consistent with that shown in Figure 3(b). When the error was high, the effect strength was almost zero.
![]()
Table 1. Effects specification of the model.
![]()
Figure 3. Effect strength of tide on the formation resistivity and calculation error distribution.
Figure 3(d) shows that the channel of seawater intrusion in this region was mainly at the electrode spacing range of 5 - 12.5 m, with the center of the intrusion channel at the electrode depth of 7.5 m. Because the original formation contains brine formation in ancient geological history, on the right side of the profile, the β value was negative and decreased along the direction of seawater intrusion (0.132 - 0). This indicates that as the tidal level increased, seawater intruded gradually, and the diving layer level increased gradually. Moreover, the formation water content increased, decreasing the formation resistivity. On the left side of the profile, because the original formation salinity is higher than that of seawater, as the tidal level increased, seawater intruded. Although the increasing of underground water level increased the formation water content, the formation resistivity increased, because seawater intrusion decreased the formation salinity. Therefore, the β value increased from 0 to 0.29. In the middle of the profile, the β value was almost zero. This indicates that the two effects offset each other. At the bottom of the profile, because of the impermeable barrier layer, the tide has no effect on the formation resistivity.
6. Conclusion
In this study, the high-density resistivity method was applied to measure the formation resistivity, and the results were analyzed by the panel data method. Up to date, the results indicate that 1) the formation resistivity in coastal area was affected by the tidal level significantly, particularly in the seawater intrusion channel, indicating that it is possible to analyze the tide effect on the groundwater in coastal area by formation resistivity; 2) because of the presence of a brine layer in the south bank of Laizhou Bay, the effects of the tidal level on the formation resistivity in the left and right sides of the section were opposite. On the right side of the profile, the tidal level has a negative correlation with the formation resistivity, and the effect strength decreases along the direction of seawater intrusion. On the left side of the profile, the tidal level has a positive correlation with the formation resistivity, and the effect increases along the direction of seawater intrusion. The effect strength of tidal fluctuation on formation resistivity varied between 0.132 and 0.29.
Acknowledgements
This research was supported by National Natural Science Foundation of China (41406072), “State Oceanic Research Project for Public Benefit” (201105020).