On the Cohomological Derivation of Yang-Mills Theory in the Antifield Formalism ()
1. Introduction
Dirac’s pioneering approach [1] [2] [3] has been used for constrained systems in quantum field theory [4] [5] [6] . This approach allowed us to construct the action in either Lagrangian or Hamiltonian forms [7] [8] , while both of them are equivalent [9] . In this way, the Hamiltonian quantization is derived using canonical variables (coordinate and momentum) involving constrained dynamics [10] - [15] . Physical variables of a constrained system possess gauge invariance and locally independent symmetry. The gauge symmetry introduces some arbitrary time independent functions to the Hamilton’s equations of motion. We notice that all canonical variables are not independent. Therefore, some conditions for canonical variables are required to be imposed, i.e., the first- and second-class constraints. Furthermore, the framework should be generalized to include both commutative (bosonic) and anticommutative (fermionic) variables in constrained systems.
To generalize constrained systems for canonical conditions and (anti-)com- mutative variables, Becchi, Rouet, Stora [16] [17] [18] , and Tyutin [19] developed the BRST formalism to extend the gauge symmetry in terms of the BRST differential and co-/homological classes. The aim was to replace the original gauge symmetry with the BRST symmetry. Noting that the gauge symmetry can be constructed from a nilpotent derivation, so the gauge action is invariant under a nilpotent symmetry, called the BRST symmetry. By replacing the original gauge symmetry with the BRST symmetry, antifield, ghosts, and antighosts are introduced for each gauge variable [20] [21] . It yields a generalized framework for solutions of the equations of motion [22] [23] . Moreover, BRST cohomology extended by the antifield formalism [23] - [30] allowed us to construct all consistent interactions among the fields using coupling deformations of the master equation [31] [32] . The BRST-antifield formalism appears as efficient mathematical tool to analyze the consistent interactions, and has been applied to many gauge models, e.g., Yang-Mills model [33] , topological Yang-Mills model [34] , 5-D topological BF model [35] , and 5-D dual linearized gravity coupled to topological BF model [36] .
In this paper, we briefly review the construction of all consistent interactions of the free Yang-Mills theory determined from all coupling deformations of the master equation. We see that the resulting action presents deformed structures of the gauge transformation and yields a commutator for it. In Section 2, the BRST differential and the antifield formalism are introduced. Section 3 introduces the consistent interactions among the fields. We consider the BRST coupling deformations of the master equations in the antifield formalism in Section 4. In Section 5, we demonstrate its application to the massless Yang-Mills theory by calculating all several order deformation of the master equation. Section 6 presents a conclusion.
2. BRST Differential
The gauge invariant in a phase space implies that the smooth phase space 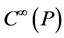 is substituted by the smooth manifold of the constraint surface
is substituted by the smooth manifold of the constraint surface 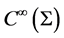 while the elements of
while the elements of 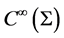 vanish due to the longitudinal exterior derivative on manifold
vanish due to the longitudinal exterior derivative on manifold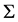 . The manifold
. The manifold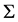 , which is embedded in a phase space and a set of vectors tangent to
, which is embedded in a phase space and a set of vectors tangent to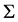 , and is closed on it, presents the definition of the gauge orbits. It manifests the presentation of a nilpotent derivation
, and is closed on it, presents the definition of the gauge orbits. It manifests the presentation of a nilpotent derivation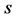 , the so-called BRST differential, that includes an algebra involving
, the so-called BRST differential, that includes an algebra involving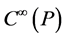 , where the cohomology of
, where the cohomology of 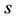 indicates that the gauge transformations of the constraint surface
indicates that the gauge transformations of the constraint surface 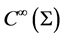 are constant along the gauge orbits (denoted by
are constant along the gauge orbits (denoted by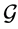 ).
).
The reduced space, by taking 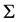 over gauge orbits, denote by algebra
over gauge orbits, denote by algebra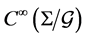 , includes all variables of the gauge invariant. However, it is not possible to construct
, includes all variables of the gauge invariant. However, it is not possible to construct 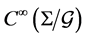 from physical observables, as one cannot solve equations defining
from physical observables, as one cannot solve equations defining 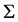 and trace the gauge orbits
and trace the gauge orbits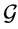 . Hence, the BRST symmetry should be used to reformulate the physical observables in a convenient approach. To construct the BRST differential
. Hence, the BRST symmetry should be used to reformulate the physical observables in a convenient approach. To construct the BRST differential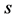 , two auxiliary derivations
, two auxiliary derivations 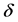 and
and ![]() are introduced. The differential of the first derivation
are introduced. The differential of the first derivation ![]() is called the Koszul-Tate differential that yields a resolution of the smooth manifold of the constraint surface
is called the Koszul-Tate differential that yields a resolution of the smooth manifold of the constraint surface![]() . The second differential is called the longitudinal differential
. The second differential is called the longitudinal differential ![]() along the gauge orbits in such its zeroth cohomology group provides the functions on the surface
along the gauge orbits in such its zeroth cohomology group provides the functions on the surface ![]() being constant along the gauge orbits
being constant along the gauge orbits![]() . Hence, the BRST differential
. Hence, the BRST differential ![]() is decomposed into [22] [23] [27]
is decomposed into [22] [23] [27]
![]() (1)
(1)
whose cohomology is equal to the cohomology of the longitudinal differential![]() , while the Koszul-Tate differential
, while the Koszul-Tate differential ![]() restricts it to the constrains surface
restricts it to the constrains surface![]() . Note that the BRST symmetry acts as a general odd derivation on the original fields and some auxiliary fields (antifields and ghosts), which are equipped for any
. Note that the BRST symmetry acts as a general odd derivation on the original fields and some auxiliary fields (antifields and ghosts), which are equipped for any ![]() and
and ![]() with Grassmann parity
with Grassmann parity ![]() and
and![]() :
:
![]() (2)
(2)
![]() (3)
(3)
where ![]() or 1 for bosonic (commutative) or fermionic (anticommutative) variable
or 1 for bosonic (commutative) or fermionic (anticommutative) variable![]() , respectively.
, respectively.
Any nilpotent derivation has a degree in a ![]() -grading space denoted by
-grading space denoted by
![]() (4)
(4)
The positive degree of the differential ![]() increases the grading while the negative degree decreases it, i.e.
increases the grading while the negative degree decreases it, i.e. ![]() depending on the degree of the differential operator. The grading of
depending on the degree of the differential operator. The grading of ![]() is the so-called ghost number (
is the so-called ghost number (![]() ), equal to one, consists of the pureghost number (
), equal to one, consists of the pureghost number (![]() ) and the antighost number (
) and the antighost number (![]() ):
):
![]() (5)
(5)
with the following property
![]() (6)
(6)
where the operators ![]() and
and ![]() stand for the pureghost and antighost numbers, respectively. For the Koszul-Tate differential
stand for the pureghost and antighost numbers, respectively. For the Koszul-Tate differential ![]() and the longitudinal differential
and the longitudinal differential![]() , we get:
, we get:
![]() (7)
(7)
such![]() . The differentials
. The differentials ![]() and
and ![]() increase the ghost number by one unit. The differential
increase the ghost number by one unit. The differential ![]() reduces the antighost number, but maintains the pureghost number, whereas the differential
reduces the antighost number, but maintains the pureghost number, whereas the differential ![]() increases the pureghost number, but maintains the antighost number.
increases the pureghost number, but maintains the antighost number.
The cohomology algebra of the differential ![]() is
is![]() , where the elements of the kernel subspace,
, where the elements of the kernel subspace, ![]() , are closed and vanish via the differential
, are closed and vanish via the differential![]() :
:
![]() (8)
(8)
while the elements of its image subspace, ![]() , are exact:
, are exact:
![]() (9)
(9)
The cohomology algebra of![]() , denoted by
, denoted by ![]() (
(![]() is a cohomology degree), exists if its degree is positive, whereas its homology algebra, denoted by
is a cohomology degree), exists if its degree is positive, whereas its homology algebra, denoted by![]() , has a negative degree. The co-/homology with the grading algebra then reads as follows
, has a negative degree. The co-/homology with the grading algebra then reads as follows
![]() (10)
(10)
If the co-/homology ![]() is zero, the differential
is zero, the differential ![]() is called to be acyclic in a degree of
is called to be acyclic in a degree of![]() .
.
The zeroth cohomology group of the BRST differential ![]() leads to Equation (3), the essential aspect of the BRST symmetry, that implies the vanishing squares of its derivations
leads to Equation (3), the essential aspect of the BRST symmetry, that implies the vanishing squares of its derivations ![]() and
and![]() :
:
![]() (11)
(11)
and also their anticommutation:
![]() (12)
(12)
It means that the Koszul-Tate differential ![]() commutes with the longitudinal differential
commutes with the longitudinal differential![]() .
.
The generator of the Koszul-Tate complex may be chosen in an equal number of freedom as the generator of the longitudinal exterior complex. It follows that they are canonically conjugate in the extended space of original and new generators of ![]() and
and![]() . This implies that the BRST transformation maintains a canonical transformation in the BRST complex space
. This implies that the BRST transformation maintains a canonical transformation in the BRST complex space ![]() through a bracket structure:
through a bracket structure:
![]() (13)
(13)
which is called the Poisson bracket and defined as follows:
![]() (14)
(14)
where ![]() and
and ![]() are positions and canonical momenta of a Hamiltonian system, respectively.
are positions and canonical momenta of a Hamiltonian system, respectively.
Equation (13) represents the BRST symmetry in the Hamiltonian formalism. The choice of ![]() as canonical transformation manifests the BRST symmetry where the canonical variables remain unchanged under transformation. The fermionic charge
as canonical transformation manifests the BRST symmetry where the canonical variables remain unchanged under transformation. The fermionic charge ![]() is called the BRST generator for the Hamiltonian formalism. Applying the Jacobi identity to the Poisson bracket and the nilpotency definition of the BRST differential yields:
is called the BRST generator for the Hamiltonian formalism. Applying the Jacobi identity to the Poisson bracket and the nilpotency definition of the BRST differential yields:
![]() (15)
(15)
which is the master equation of the BRST generator in the Hamiltonian formalism.
3. Consistent Interactions
To understand the consistent interactions among fields with a gauge freedom, we begin our study with a Lagrangian action:
![]() (16)
(16)
where the action ![]() is local functional of the fields
is local functional of the fields ![]() and their Lorentz covariant derivatives.
and their Lorentz covariant derivatives.
The equations of motion then read ![]() where
where ![]() is functional derivatives. The action
is functional derivatives. The action ![]() possesses generic free gauge symmetries
possesses generic free gauge symmetries
![]() (17)
(17)
The equations of motion is then determined from the action principle:![]() .
.
Let consider the deformations of the action in such a way
![]() (18)
(18)
that implies the deformation of gauge symmetries as
![]() (19)
(19)
This provides the deformed gauge transformations:
![]() (20)
(20)
Equation (18) and Equation (19) lead to the following expression:
![]() (21)
(21)
Hence, the deformations by their orders are as follows:
![]() (22)
(22)
which define the deformed gauge transformations that close on-shell for the interacting action, the so-called consistent interactions, while the original gauge transformations are reducible [28] .
Assume that the gauge fields of consistent interactions are trivially defined to be the following sum:
![]() (23)
(23)
we then obtain
![]() (24)
(24)
which does not manifest an exact interacting theory. A theory is strict if the consistent deformations are merely proportional to its free theory action ![]() up to the redefinition of the gauge fields. Thus, the interaction is formulated as follows:
up to the redefinition of the gauge fields. Thus, the interaction is formulated as follows:
![]()
where charges ![]() in the
in the ![]() order of the coupling constants
order of the coupling constants ![]() are given by
are given by
![]() (25)
(25)
It represents the unperturbed action by charges of the coupling constants.
4. BRST Deformations of the Master Equation
Let us consider the gauge transformation defined by the Equation (17). The classical fields ![]() possesses the ghost number zero. It implies an ghost
possesses the ghost number zero. It implies an ghost ![]() associated to ghost number one, as well as the one-level ghost of ghost
associated to ghost number one, as well as the one-level ghost of ghost ![]() have number two, etc., i.e.
have number two, etc., i.e.
![]() (26)
(26)
which have the following ghost numbers, ![]() , and Grassmann parities,
, and Grassmann parities,![]() :
:
![]() (27)
(27)
It also implies antifields ![]() and antighosts
and antighosts ![]() of opposite Grassmann parity with the following ghost numbers,
of opposite Grassmann parity with the following ghost numbers, ![]() , and Grassmann parities,
, and Grassmann parities, ![]() , respectively:
, respectively:
![]() (28)
(28)
![]() (29)
(29)
The presentation of the gauge variables is therefore provided by
![]() (30)
(30)
where a set of fields ![]() includes the original fields, the ghost, and the ghosts of ghosts, and
includes the original fields, the ghost, and the ghosts of ghosts, and ![]() includes the their corresponding antifields.
includes the their corresponding antifields.
The BRST symmetry is a canonical transformation, and defined by an antibracket structure:
![]() (31)
(31)
where ![]() is the canonical generators, and the antibracket (see appendix 7.1) is defined in the space of fields
is the canonical generators, and the antibracket (see appendix 7.1) is defined in the space of fields ![]() and antifields
and antifields ![]() as follows [24] :
as follows [24] :
![]() (32)
(32)
The Grassmann parity and ghost number of the antibracket are, respectively:
![]() (33)
(33)
![]() (34)
(34)
The antifields are now considered as mathematical tool to construct the BRST formalism. The solution can be interpreted as source coefficient for BRST transformation, i.e., an effective action in the theory.
The fields and antifields establish the solution ![]() of the classical master equation for consistent interactions [31] ,
of the classical master equation for consistent interactions [31] ,
![]() (35)
(35)
Section 2 presented the master Equation (15) of the BRST generator in the Hamiltonian formalism. The gauge structure is now constructed through the solution ![]() of the master equation in the antifield formalism by [24] [25] [34]
of the master equation in the antifield formalism by [24] [25] [34]
![]() (36)
(36)
This shows the consistency of the gauge transformations. The master Equation (36) includes the closure of the gauge transformations, the higher-order gauge identities, and the Noether identities. The master equation maintains the consistent specifications on ![]() and
and![]() .
.
Substituting the definition (35) into the master Equation (36) yields
![]() (37)
(37)
We then derive
![]() (38)
(38)
which are simplified as follows [31] [36] [37] [38]
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
![]() (42)
(42)
![]() (43)
(43)
![]() (44)
(44)
![]()
the so-called deformations of the master equation [31] [32] .
The Equation (40) implies that ![]() is a cocycle for the free differential defined by
is a cocycle for the free differential defined by![]() , i.e.,
, i.e., ![]() is a coboundary,
is a coboundary,![]() . The Equation (39) hence corresponds to
. The Equation (39) hence corresponds to![]() . The Equation (41) indicates that
. The Equation (41) indicates that ![]() is trivial in
is trivial in![]() , and
, and ![]() is mapped trivially into
is mapped trivially into ![]() by the antibracket. Furthermore, the higher orders
by the antibracket. Furthermore, the higher orders ![]() mapped into
mapped into ![]() are trivial, and provide the existence of the terms
are trivial, and provide the existence of the terms ![]() etc, up to an element of
etc, up to an element of![]() . So, the
. So, the ![]() orders
orders ![]() freely link the interaction of an arbitrary element of
freely link the interaction of an arbitrary element of![]() .
.
The free gauge invariant action ![]() and the gauge transformations can be retrieved from
and the gauge transformations can be retrieved from
![]() (45)
(45)
by setting
![]() (46)
(46)
It provides the solution ![]() of the classical master equation for field gauge symmetries,
of the classical master equation for field gauge symmetries,
![]() (47)
(47)
The BRST differential ![]() is now defined by
is now defined by ![]() through the antibracket,
through the antibracket,
![]() (48)
(48)
Using the definitions (48), the deformations of the master equation are rewritten as follows:
![]() (49)
(49)
which are the deformations of the master equation in terms of the BRST differential![]() .
.
5. BRST Cohomology of the Free Yang-Mills Theory
Let us consider a set of ![]() potentials
potentials ![]() described by the abelian action in terms of the free (massless) Lagrangian action
described by the abelian action in terms of the free (massless) Lagrangian action
![]() (50)
(50)
where ![]() is the abelian field potential,
is the abelian field potential, ![]() is the spacetime dimension, strictly
is the spacetime dimension, strictly![]() , since the theory has no local degree of freedom in two dimensions, and the abelian field strengths
, since the theory has no local degree of freedom in two dimensions, and the abelian field strengths ![]() is defined by
is defined by
![]() (51)
(51)
in such a way
![]() (52)
(52)
where ![]() is the
is the ![]() invariant flat metric in Minkowski space with the particular hermitian representation of the Clifford algebra
invariant flat metric in Minkowski space with the particular hermitian representation of the Clifford algebra![]() , and
, and ![]() is a given symmetric invertible matrix with following properties
is a given symmetric invertible matrix with following properties
![]() (53)
(53)
The gauge transformation with the free equation of motion,
![]() (54)
(54)
manifests an irreducible transformation by
![]() (55)
(55)
while
![]() (56)
(56)
The differential operator ![]() is determined by the structure
is determined by the structure ![]() of the gauge transformations of an abelian algebra. The action (50) is close according to an abelian algebra, and invariant under the gauge transformation (55). The gauge invariant (55) eliminates unphysical terms, i.e. the longitudinal and temporal degrees of freedom.
of the gauge transformations of an abelian algebra. The action (50) is close according to an abelian algebra, and invariant under the gauge transformation (55). The gauge invariant (55) eliminates unphysical terms, i.e. the longitudinal and temporal degrees of freedom.
The implementation of the BRST transformation in the minimal sector provides the field![]() , its ghost
, its ghost![]() , and their antifields
, and their antifields ![]() and
and ![]() with the respective Grassmann parities, antighost, pureghost, and (total) ghost numbers,
with the respective Grassmann parities, antighost, pureghost, and (total) ghost numbers,
![]() (57)
(57)
which can schematically be illustrated:
![]()
We calculate the BRST-differential ![]() that decomposes into the sum of two differentials, the Koszul-Tate differential
that decomposes into the sum of two differentials, the Koszul-Tate differential ![]() and the longitudinal differential
and the longitudinal differential ![]() along the gauge orbits. Both
along the gauge orbits. Both ![]() and
and ![]() are derivations, and commute with
are derivations, and commute with![]() , and acting on
, and acting on![]() ,
, ![]() ,
, ![]() , and
, and ![]() via [33] [39]
via [33] [39]
![]()
The classical master Equation (47) of the action (50) holds the minimal solution (45) in such a way
![]() (58)
(58)
5.1. First-Order Deformation
We now consider the deformed solution of the master equation for the action (50) smoothly in the coupling constant ![]() that brings to the solution (58), while the coupling constant
that brings to the solution (58), while the coupling constant ![]() vanishes. In Section 4, we noticed that the first-order deformation (
vanishes. In Section 4, we noticed that the first-order deformation (![]() ) of the master equation satisfies the solution
) of the master equation satisfies the solution![]() , where
, where ![]() is bosonic (commutative) function with ghost number zero.
is bosonic (commutative) function with ghost number zero.
Let us assume
![]() (59)
(59)
where ![]() is a local function. Then, the first-order deformation,
is a local function. Then, the first-order deformation, ![]() , takes the local form
, takes the local form
![]() (60)
(60)
![]() (61)
(61)
where ![]() is a local current that manifests the non-integrated density of the first-order deformation corresponding to the local cohomology of
is a local current that manifests the non-integrated density of the first-order deformation corresponding to the local cohomology of ![]() in ghost number zero,
in ghost number zero, ![]() , where
, where ![]() is the exterior spacetime differential.
is the exterior spacetime differential.
To evaluate Equation (60), we assume
![]() (62)
(62)
![]() (63)
(63)
where ![]() are some local currents. Substituting (62) and (63) into (60) yields
are some local currents. Substituting (62) and (63) into (60) yields
![]() (64)
(64)
obviously
![]() (65)
(65)
They can be decomposed on the several orders of the antighost number:
![]() (66)
(66)
The positive antighost number are strictly given as replacement for the first expression [35] :
![]() (67)
(67)
To proof it, let us consider ![]() as the elements with pureghost number
as the elements with pureghost number ![]() of a basis in the polynomial space. The generic solution of (67) then takes the form
of a basis in the polynomial space. The generic solution of (67) then takes the form
![]() (68)
(68)
while
![]() (69)
(69)
The objects ![]() obviously are nontrivial in
obviously are nontrivial in ![]() the so-called invariant polynomials. In other words, the strict positive antighost numbers provide trivially the cohomology of the exterior differential
the so-called invariant polynomials. In other words, the strict positive antighost numbers provide trivially the cohomology of the exterior differential ![]() in the space of invariant polynomials
in the space of invariant polynomials![]() . Hence,
. Hence, ![]() reduces to
reduces to ![]() (see [35] for general proof).
(see [35] for general proof).
Moreover, ![]() may exclusively be reduced to
may exclusively be reduced to ![]() -exact terms
-exact terms
![]() (70)
(70)
corresponding to a trivial definition, which states![]() . This result is obviously given by the second-order nilpotency of
. This result is obviously given by the second-order nilpotency of ![]() that implies the unique solution of (67) up to
that implies the unique solution of (67) up to ![]() -exact contributions, i.e.
-exact contributions, i.e.
![]() (71)
(71)
![]() (72)
(72)
Hence, the non-triviality of the first-order deformation ![]() requires the cohomology of the exterior longitudinal derivative
requires the cohomology of the exterior longitudinal derivative ![]() in pureghost number equal to
in pureghost number equal to![]() , i.e.
, i.e.![]() . To solve (66), it is necessary to provide the cohomology of
. To solve (66), it is necessary to provide the cohomology of ![]() and
and![]() ,
, ![]() and
and![]() :
:
![]() (73)
(73)
where
![]() (74)
(74)
For an irreducible linear situation, where gauge generators are field independent, we assume that
![]() (75)
(75)
where ![]() manifests the local cohomology of the Koszul-Tate differential
manifests the local cohomology of the Koszul-Tate differential![]() , while antighost number is
, while antighost number is ![]() and pureghost number vanishes. In this case (
and pureghost number vanishes. In this case (![]() ), we obtain
), we obtain
![]() (76)
(76)
The first-order deformation up to antighost number two are:
![]() (77)
(77)
The ![]() is generated by arbitrarily smooth functions in the form (68), with
is generated by arbitrarily smooth functions in the form (68), with ![]() from
from ![]() and
and ![]() denote the elements with pureghost number two of a basis in the polynomial space, i.e.,
denote the elements with pureghost number two of a basis in the polynomial space, i.e.,
![]() (78)
(78)
where ![]() is the local cohomology of the Koszul-Tate differential
is the local cohomology of the Koszul-Tate differential ![]() with antighost number
with antighost number ![]() in the invariant polynomial space.
in the invariant polynomial space.
We now consider the Koszul-Tate differential ![]() and the exterior longitudinal differential
and the exterior longitudinal differential ![]() in the action (58):
in the action (58):
![]()
![]()
The local cohomology of the exterior longitudinal derivative ![]() in pureghost number one,
in pureghost number one, ![]() has one ghost
has one ghost![]() , while
, while ![]() has two ghosts
has two ghosts![]() , i.e.
, i.e.
![]() (79)
(79)
From (79), we then solve
![]()
by
![]() (80)
(80)
where ![]() contains the structure constants of a non-abelian algebra coupling the Yang-Mills fields, and it is antisymmetric on indices
contains the structure constants of a non-abelian algebra coupling the Yang-Mills fields, and it is antisymmetric on indices![]() :
:
![]() (81)
(81)
The expression ![]() is solved by taking the Koszul-Tate differential
is solved by taking the Koszul-Tate differential ![]() from (80):
from (80):
![]() (82)
(82)
We simply notice that
![]() (83)
(83)
This indicates
![]() (84)
(84)
To obtain![]() , we solve
, we solve ![]() by taking the Koszul-Tate differential
by taking the Koszul-Tate differential ![]() from
from![]() :
:
![]() (85)
(85)
The last term in above relation vanishes, i.e.
![]()
since
![]()
while
![]()
Therefore, we derive
![]() (86)
(86)
It shows
![]() (87)
(87)
The results for the first-order deformation are summarized as follows:
![]() (88)
(88)
Finally, we derive
![]() (89)
(89)
The first-order deformations of the solution (![]() ) of the master equation were determined for the action (58). It is seen that gauge generators are field independent, and are reduced to a sum of terms with antighost numbers from zero to two.
) of the master equation were determined for the action (58). It is seen that gauge generators are field independent, and are reduced to a sum of terms with antighost numbers from zero to two.
5.2. Higher-Order Deformations
We now consider the higher-order deformations of the master equation for the action (50). The second-order deformation (![]() ) of the master equation are determined from the solution
) of the master equation are determined from the solution![]() . Let us assume that
. Let us assume that
![]() (90)
(90)
that takes the local form
![]() (91)
(91)
Using the Equation (88) from Section 5.1, we calculate![]() :
:
![]()
while employing the following relations
![]() (92)
(92)
![]() (93)
(93)
and the definitions
![]() (94)
(94)
![]() (95)
(95)
They lead to the following expression![]() :
:
![]()
that is reduced to
![]()
We then decompose ![]() into the following terms,
into the following terms,
![]() (96)
(96)
namely,
![]() (97)
(97)
![]() (98)
(98)
![]() (99)
(99)
We also define
![]() (100)
(100)
From (91), it follows a set of equations
![]() (101)
(101)
![]() (102)
(102)
![]() (103)
(103)
Equations (99) and (101) imply
![]() (104)
(104)
and
![]() (105)
(105)
The later expression is called the Jacobi identity. Similarly, we obtain
![]() (106)
(106)
So, the Equation (103) remains to be solved:
![]() (107)
(107)
We solve it by substituting the exterior longitudinal differential ![]() of potentials
of potentials ![]() (
(![]() ):
):
![]()
Accordingly, we derive
![]()
Hence, the second-order deformations becomes
![]() (108)
(108)
The Jacobi identity (105) obviously implies
![]()
Similarly, all deformations with orders higher than the second-order completely vanish:
![]()
As a result, the solution to the deformations becomes![]() , that corresponds to the following Yang-Mills theory:
, that corresponds to the following Yang-Mills theory:
![]() (109)
(109)
We have determined the Yang-Mills theory from the first- and second-order deformations of the master equation. The solutions of the master equation, which entirely include the gauge structures, are decomposed into terms with the antighost numbers from zero to two. In other words, the part with the antighost number equal to zero represents the Lagrangian action, while the antighost number one is proportional to the gauge generators. The terms with higher antighost numbers provide the reducibility functions, where the on-shell relations become linear components in the ghosts for ghosts. It is shown that all functions with order higher than second vanish in this model.
5.3. Interacting Theory
Let us consider the Equation (109) and identify the entire gauge structure of the Lagrangian model that describes all consistent interactions in the ![]() -dimensional free Yang-Mills theory.
-dimensional free Yang-Mills theory.
The antighost number zero of (109) shall provide the Lagrangian action of the interacting theory:
![]() (110)
(110)
Accordingly, the Yang-Mills theory is characterized by the following non- abelian action:
![]() (111)
(111)
where the non-abelian field strengths ![]() is defined by
is defined by
![]() (112)
(112)
and ![]() is the gauge-invariant that provides the gauge symmetry of the Yang-Mills theory as follows
is the gauge-invariant that provides the gauge symmetry of the Yang-Mills theory as follows
![]() (113)
(113)
So, the commutator among the deformed gauge transformations becomes:
![]() (114)
(114)
The gauge symmetry remains abelian to order![]() , and satisfies the equation of motion
, and satisfies the equation of motion
![]() (115)
(115)
The invariance of the action under the gauge transformations (113) is also obtained by the Noether identities
![]() (116)
(116)
The antighost number one of the deformation of the master equation allows to identify the gauge transformations (113) of the action (110) by substituting the ghost ![]() with gauge parameter
with gauge parameter![]() . The antighost number two in (109) reads the complete gauge structure of the so-called interacting theory that determines the commutator (114) among the deformed gauge transformations.
. The antighost number two in (109) reads the complete gauge structure of the so-called interacting theory that determines the commutator (114) among the deformed gauge transformations.
6. Conclusion
In this paper, we reviewed deformed gauge transformations in the framework of the BRST-antifield formalism characterized by the antibracket that acts similar to the Poisson bracket in the Hamiltonian formalism. We provided the BRST cohomology of the consistent interactions through several order deformations of the master equation. The BRST-antifield formalism in the cohomological space provides the generalized framework of consistent interactions among fields with a gauge freedom by any types of invariant action. We see that higher order deformations could be neglected due to non local interactions and their obstruction of consistent local couplings, which are associated with the anomalous gauge quantization. We demonstrated its functions by applying the BRST-antifield formalism to the ![]() -dimensional, free Yang-Mills theory. All deformations of the master equation for the massless Yang-Mills model were calculated by using the cohomological groups
-dimensional, free Yang-Mills theory. All deformations of the master equation for the massless Yang-Mills model were calculated by using the cohomological groups![]() , of the BRST differential. The first-order deformation is provided by the cohomological group
, of the BRST differential. The first-order deformation is provided by the cohomological group![]() , whereas the second-order deformation given by the cohomological group
, whereas the second-order deformation given by the cohomological group ![]() obstructs all higher-order deformations. The results show that the deformations can be synthesized by the conception that all orders higher than two are trivial, while gauge generators are imposed to be field independent,
obstructs all higher-order deformations. The results show that the deformations can be synthesized by the conception that all orders higher than two are trivial, while gauge generators are imposed to be field independent,![]() . The deformations stopped at the second-order of the coupling constants characterize the consistent interactions, which maintain the equation of motion, and provide the entire gauge structure of the interacting Yang-Mills theory.
. The deformations stopped at the second-order of the coupling constants characterize the consistent interactions, which maintain the equation of motion, and provide the entire gauge structure of the interacting Yang-Mills theory.
Acknowledgements
The author thanks the editor and the referee for their comments. Research of A. Danehkar is funded by the EU contract MRTN-CT-2004-005104. This support is greatly appreciated.
Appendix
Antibracket Structure
For a function ![]() in a generic space, commutative or anticommutative, we state:
in a generic space, commutative or anticommutative, we state:
![]() (117)
(117)
The left derivative ![]() is an ordinary derivative (left to right). The right derivative
is an ordinary derivative (left to right). The right derivative ![]() is the derivative action from right to left.
is the derivative action from right to left.
For any ![]() in a generic space, we get
in a generic space, we get
![]() (118)
(118)
Considering Equation (32) and Equation (118), it follows that
![]()
Assuming![]() , one can find
, one can find
![]() (119)
(119)
For bosonic (commutative) and fermionic (anticommutative) variables, we have
![]() (120)
(120)
For any![]() , we have
, we have
![]() (121)
(121)
Furthermore, the antibracket has the following properties:
![]() (122)
(122)
![]() (123)
(123)
![]() (124)
(124)