Symmetry in Equations of Motion between the Atomic and Astronomical Models

Abed El Karim S. Abou Layla

Independent Researcher, Gaza City, Palestine.

DOI: 10.4236/jhepgc.2017.32028                

Abstract

In this paper, we are going to find out a simple way yet extraordinary to the equation of motion of electric charge under the influence of a central force. We’ll find that it is the same as the formula of the common equation of motion in the theory of general relativity which controls the motion of planets around the sun; thus, every electron orbiting around the nucleus has a perihelion which revolves same as Mercury perihelion yet faster 2000 times according to Hydrogen atom, assuming that hydrogen has a perihelion. That is to say, when Mercury perihelion takes three million years to complete a full cycle around the sun, we find that Hydrogen perihelion (here we mean the classical model of atom, not quantitative model of it) revolves around the nucleus at 1.05 × 1012 cycle per second. In addition, the radiation passing near the nucleus deviates same as the deflection of light passing near the sun yet with a greater value according to how close the radiation is from the nucleus, as shown in the discussion. We discussed briefly (but differently) the definition of black holes to affirm symmetry principle between the atomic and astronomical models. Symmetry in equations of motion of a body in the atomic and astronomical models indicates that the Advance of Mercury’s Perihelion, deflection of light passing near the sun, and the definition of black holes are the ABCs of classical physics; however, they are not considered as reliable evidences on the soundness of the principle on which the theory of general relativity is built on, in the presence of a contradiction between the definition of gravity in the general relativity and in the electromagnetic theory.

Keywords

Relativity, Mercury’s Perihelion, Deflection of Light, Black Holes, Khromatic Theory

1. Introduction

Symmetry between electromagnetic and gravitational laws has been discussed in physics since ago. The subject matter lately gained some momentum because it is straightforward and easy to use for obtaining important findings in physics even though there is no theoretical evidence accounting for this symmetry.

Since reference to symmetry topic in the nineteenth century by Holzmüller and Tisserand [1] till this day, a lot of books and researches supporting this approach has been published everywhere because they managed to describe some cosmic phenomena which motivated the supporters to continue publishing their researches, part of which discredited the theory of general relativity; however, it was defended and verified by its supporters, asserting that they can deduce some gravitational field laws that assimilate to the electric field even though there is a contradiction in principle between the definition of gravity according to the general relativity and the electromagnetic theory. General Relativity states that gravity is a result of time-space curvature due to the existence of material. On contrast, Maxwell equations consider electromagnetism as a kind of “force field” that flows through the four-dimensional universe.

In this paper, we are not discrediting the theory of general relativity, but we are proving that the evidences verifying the soundness of the theory are insufficient in the presence of the aforementioned contradiction. Perihelion precession, deflection of light passing near to the sun, discovery of black holes, and the existence of gravitational waves, discovered recently by LIGO Observatory on 11th Feb, 2016, are cosmic phenomena which can be theoretically proved through classical method through symmetry principle between the electronic and gravitational fields, far away from the general relativity and its hypotheses.

In this paper, we are going to generalize the equation of Motion of a charged particle in the field of central force influencing it through a new definition, which is titled “Radiation Mass”. We’ll find that the generalized equation matches Mercury common equation of motion deduced through the theory of general relativity. Thus, we prove that the cosmic phenomena shown above are not exclusive to the astronomical models but also to the atomic models.

Through the discussion, we chose to apply the generalized equation of motion on the old classical model of hydrogen atom, presuming that it has a perihelion at the first orbit. By calculating the advance of this Perihelion and deflection of radiation passing near to the nucleus, we are going to compare the findings with those of Mercury to only show the vast difference between the atomic and the astronomical models, which should not be taken to mean that we go back to physics 100 years ago back.

Finally, we would like to explain that the principle of symmetry doesn’t exist only in the electronic and gravitational field, but it also includes any force in the nature that has field strength that can be calculated at any point on the field of this strength. This was proved in “The Khromatic Theory” [2] which unifies the electronic and gravitational fields, which will be published in a series of subsequent researches.

2. Radiation Mass Definition

The research is based on one of the findings contained in “The Khromatic theory” which states:

“A body acquires an additional mass equivalent to its potential energy whilst moving vertically over the force field that influences it.”

In the previous statement, we deduce that the static bodies or bodies moving in a parallel movement to the lines of force dose not acquire any additional mass. By calling the additional mass as radiation mass (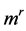), we can formulate the relationship between the potential energy and the additional mass as follows:

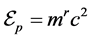(2.1)

where c is light speed. Thus, radiation mass for the bodies moving rotationally equals:

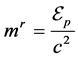
Consequently, anybody moves in orbital speed 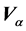acquires an additional radiation momentum 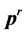equivalent to its value, through this equation:

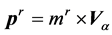(2.2)

while the static objects or objects moving in a transitional motion towards force center, its radiation mass equals zero; thus the body does not acquire any additional momentum in this direction.

The Equation (2.2) considered as the dynamic formula for the radiation momentum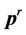, while the corresponding electromagnetic formula can be formulated as follows:

so

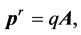
as

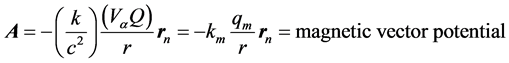
q: The charge of particle (c);

q_m: Pole strength (A×m);

k_m: Is a Magnetic constant of proportionality (N/A²).

3. Relationship between Radiation Mass and Inertial Mass

Let’s assume that r is vector position of a charge q moving in a circular track around the central charge Q, supposing that k stands for coulomb constant, so charge potential energy equals:

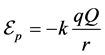
Consequently

Assuming that

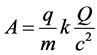(3.1)

We obtain this formula

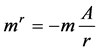(3.2)

Through the latter equation, we notice that radiation mass m^r is a negative mass inversely proportional to radius r.

Thus, the ratio between the radiation and inertial masses are given through the following formula:

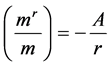(3.3)

It’s worth mentioning that the ratio between the radiation and inertial masses in the classical model of Hydrogen atom exceeds 5.3 × 10⁻⁵, while in the astronomical model of the solar system it doesn’t exceed 3 × 10⁻⁸. Thus, the square of the ratio of both masses is small enough to be neglected compared to numbers unit.

To sum up, we can express it mathematically in the following formula:

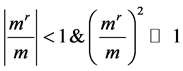
4. Finding the Total Momentum and Energy of Moving Body

Let’s assume that an orbital charge q is moving under the influence of central charge Q, and are orthogonal unit vectors representing right-handed system, speed and vector position are determined according to the following formulas:

4.1. Body’s Total Momentum p

Based on the analysis above, we know that the body moving under the influence of a central force field acquires an additional amount of momentum, which is radiation momentum amount. Accordingly, the amount of body’s total momentum p equates the sum of body’s kinetic momentum and radiation momentum according to the following formula:

(4.1)

Accordingly,

It is worth mentioning that the electromagnetic version of Equation (4.1) be in shape

which founds in some of the electromagnetic and quantum mechanics books, and knowledge in Wikipedia [3] as follows

where P is the canonical momentum; p the kinetic momentum; q point charge; A the magnetic vector potential.

4.2. Body’s Kinetic Energy ε_k

We can figure out the value of body’s kinetic energy through the following equation:

By neglecting the square ratio between the radiation and inertial masses due to its tiny value with respect to the atomic and the astronomical models as shown above, the equation goes like

Accordingly,

4.3. Body’s Total Energy ε

Whereas the total energy e the body moves with equates the sum of kinetic energy e_k and potential energy e_p, accordingly

By reformulating the latter equation in terms of inertial mass only, we obtain

5. Electro-Black Holes

We conclude from Equation (3.3) that the radiation mass is a negative inertial mass. That is to say, the additional amount of momentum, the body acquires as a result of this mass, works in reverse to the original amount of motion the body moves with.

In case both masses are equal on a certain distance r_s from the power axis called event horizon by the formula,

the body will stop moving in the vertical direction on the field of this force while continuing moving in the parallel direction of the field lines. In this condition, the body is in falling state towards the direction of the influencing axis of force.

We can deduce the exact value of event horizon as follow,

Motion amount equation looks like,

In a state of constant falling towards the center, there is no rotational speed. Thus, we obtain the following two equations

Accordingly,

However, event horizon approximate value is deduced through body’s kinetic energy equation, as follows:

By equating rotational speed index V_α to zero, we obtain the following two equations:

Accordingly,

It equates the double of event horizon exact value deduced through motion amount equation. This difference is rendered to the negligence of the square of the inertial and radiation masses while deducing kinetic energy equation which corresponds to assuming Ricci Tensor in Schwarzschild solution equals zero in the theory of general relativity.

Accordingly, Schwarzschild solution is not valid except in cases where. This confirmed by obtaining the selfsame value of event horizon through classic mechanics laws which meet this condition.

6. General Equation of an Electric Charge in the Field of Central Force Influencing it

We can Derivation of general equation of charge motion falling under the impact of central force. Assuming that,

whereas moment of momentum is a fixed amount; thus; J is a fixed amount, too. Accordingly, we obtain

Accordingly, total energy equation looks like:

By solving the last differential equations, we obtain

By doing some shortcuts, we obtain the equation of motion of the classical atomic models as follows:

7. Comparison of the Atomic and the Astronomical Models

The equation of motion that determines planets orbits around the sun in the theory of general relativity looks like,

where A is a constant given through the following equation:

By comparing both equations of the atomic and the astronomical models, we’ll find that there is an exact match in shape between them; however, the difference is in the constant formula A where there is an obvious symmetry between the two constants so that if we replace the electric field constants with their equivalent in the gravitational field,

we obtain the gravitational field constant formula A; thus we proved the symmetry in equations of motion between the atomic and the astronomical models.

It is worth mentioning that it can also be proof that the generalized of the Schwarzschild space-time metric is on form

As

So, the metric has a singularity when the denominator in the first term is equal to zero:

Accordingly,

8. The Result

Movement equations and laws are identical under the influence of central force fields. In addition, we can’t distinguish between the behaviors of bodies under the influence of these powers whether it’s an electric charge or an object, etc.

9. Discussion

9.1. Calculating the Deflection of Light

Value of light path deflection derived from the equation of general motion equation, takes the following formulation [4]

where

R is the minimum distance between the trajectory of light and the center of the charge as shown in Figure 1.By neglecting the influence of the electron in the first orbit in hydrogen atom on the light beam passing near it, we can calculate the deflection of light based on the following data:

Figure 1. Showing light deflection path in the atomic model.

As follows:

It means that light path passing near hydrogen first orbit suffers an initial deflection of 43.88 seconds which increases the closer we get to the nucleus. This is a very huge amount if compared to the deflection of the light passing near the sun which suffers a deflection of 1.75 second in spite of the magnitude of sun mass in comparison to Hydrogen atom.

9.2. Calculating the Value of Perihelion Precession in the Classical Atomic Model

Solving the equation of charge motion is as follows:

Accordingly, we conclude that the value of perihelion precession (shown in Figure 2) is given by following formulation [5]

To give a rough image for the value of perihelion precession in the atomic model, we suppose that the electron of hydrogen atom has a perihelion whilst the proton is constant; by the previous application data, we can calculate this value, as follows:

Figure 2. Explaining perihelion precession in the atomic model.

In other words, for every completed cycle around the center by the electron, perihelion progresses to its orbit at 1.0037 × 10⁻³ radian, a very huge value in comparison with perihelion precession in Mercury planet, 5.02 × 10⁻⁷ radian in case we neglect the influence of other planets movement.

By comparing both values, we find that Hydrogen perihelion deflection is 2000 times bigger than its equivalent in Mercury even though Hydrogen atom is so small compared to Mercury orbit.

On the other hand, for Hydrogen perihelion to complete a full cycle around the center, the electron has to complete a number of cycles, calculated through this formula:

Accordingly, we can calculate perihelion frequency per second around Hydrogen nucleus through this formula:

As for Mercury, for the perihelion to complete a full cycle around the sun, Mercury needs to complete a number of full cycles, 1.251 × 10⁷ cycles which equal three million earth years, assuming that every Mercury cycle needs 88 earth years to complete a full cycle; thus,

By the time Hydrogen perihelion moves around the nucleus at 1.05 × 10¹² times per second, Mercury needs more than three million years for the perihelion to complete one full cycle only. This explains why it’s impossible to determine electron position at a given time while we can figure it out accurately as for the planets.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Holzmüller, G. Zeitschriftfür Mathematik und Physik 15, p. 69, 1870, F. Tisserand, Comptes Rendus 75, p. 760, 1872, and Comptes Rendus 110, p. 313, 1890.
[2]	Abou Layla, A.K. (2016) The Khromatic Theoary, Al Manra.
[3]	Wikipedia, Momentum. http://en.wikipedia.org/wiki/Momentum
[4]	Schiller, C. (2012) Motion Mountain, the Adventure of Physics. Relativity, 2, 165.
[5]	Schiller, C. (2012) Motion Mountain, the Adventure of Physics. Relativity, 2, 169.