Estimation of Tree Height and Forest Biomass Using Airborne LiDAR Data: A Case Study of Londiani Forest Block in the Mau Complex, Kenya ()
1. Introduction
Forest operations require reliable information on forest status and its evolution ( Ruiz et al., 2014 ). The main intention of forest inventories is to define the extent, assess the composition and condition of forest resources to ensure sustainable forest management, which calls for an up to date forest inventory. Forest inventory estimation begun in the middle ages ( McRoberts et al., 2010 ). Timber users ( Loetsch & Haller, 1973 ; Davis et al., 2001 ) conducted the initial forest inventories, focused on estimating growing stock volume. The role of forest have changed over time altering the demands of forest information and hence broadening the scope of National Forest Inventory.
The manual methods of forest inventories involved consumed time and cost, as an aid to this the Remote Sensing technology has been used. This technology has been used in various applications around the world: natural resource management (forest ecosystem management) for many years ( Chen et al., 2005 ), mapping, modeling and understanding of the ecosystem ( Lefsky et al., 2002 ) among others. Conventional applications of remote sensing used images from passive sensors ( Goward & Williams 1997 ) though topographical covers and weather condition influence them. In few cases, RADARSAT, obtained from active radar sensors, has been used ( Waring et al., 1995 ).
Light detection and Ranging (LiDAR), also known as Laser altimetry is an active remote sensing technique that is similar to radar but uses laser light pulses instead of radio waves ( NOAA Coastal Services Center, 2012 ) has been used to minimize the challenges. This technology determines ranges (distances) by taking the product of the speed of light and the time taken for an emitted laser to travel to a target object. The elapsed time from when a laser is emitted from a sensor and intercepts an object can be measured using either; pulsed ranging, or continuous wave ranging, where the phase change in a transmitted sinusoidal signal produced by a continuously emitting laser is converted into travel time ( Lim et al., 2003 ).
LiDAR systems have been used in different applications namely: flood risk mapping, bird population modeling, ice sheet mapping, pesticide application, econometric modeling, terrain modeling, and land cover classification, as well as an array of atmospheric and extra-terrestrial applications ( Lim et al., 2003 ). In
forestry, LiDAR remote sensing has been used in estimating forest attributes such as stand heights, biomass, crown cover density, ground elevation below the forest canopy among others. LiDAR systems produce point clouds representing the height distribution of the forest canopy, which enables one to obtain different characteristics of a complex forest stand and provide valuable information. This has led to a successful creation of forest inventories at reduced costs ( Ruiz et al., 2014 ). In Kenya, Kinyanjui et al. (2015) demonstrated that LiDAR data can be used to classify the montane forests to show height variations among agro climatic zones and human use zones. However, their work was not ground truthed and gave an estimate of tree heights in the different forests. This study was done in Londiani forest block of the Mau Ecosystem with the objective of testing the applicability of using LIDAR data in developing forest inventory data for Kenya to ease the process of collecting data using conventional forest inventory techniques which are time consuming and costly.
2. Methods
2.1. Study Area
The Mau Forest Complex which covers approximately 400,000 Ha forms the largest closed canopy forest ecosystem in Kenya ( Kinyanjui et al., 2014 ). This complex with a variety of montane forest vegetation is subdivided into 22 blocks. Londiani forest block, one of the blocks, covers an approximate area of 18,938 hectares and Nakuru, Kericho and Baringo Counties. Figure 1 shows the study area which is located between 35˚31'58"E, 35˚46'50"E, and latitudes 0˚10'30"S, 0˚0'10"N. The forest block borders Tinderet, Maji mazuri and Western Mau forest blocks of the Mau complex.
Londiani Forest block is a montane forest which ranges from 2000 m to 2900 m ASL. The Average temperatures are between 8.6˚C and 23.31˚C. The area has two rainy seasons; the long rains occurring in the months of March to May with average rainfall level of 750 mm and the short rains in October to December with an average rainfall of 423 mm. The driest months are January to February and August to September.
2.2. Data Acquisition
Data sets used in this study include ALS LiDAR data, Aerial image and Ground data from field measurements. The LiDAR data and the Aerial image were captured in February 2014 with a scanner on flight of altitude 1550 m above ground level, point density 2 pts/m2 in nadir and the ground sample distance 12 cm. This data was used to generate the Canopy Height Model (CHM), Digital Surface Model (DSM) and the Digital Elevation Model (DEM) for the study area.
2.3. Sampling Design
Stratified sampling was used based on the elevation and different forest cover types. A grid over the study area was generated with a cell size of 26.5 × 26.5 m. The cell size corresponds to the area of a reference sample plot of radius 15 m.
![]()
Figure 1. The location of Londiani Forest Block.
The allocation and selection of sampling plots was based on the elevation, forest cover types and differences in tree heights.
a) Image classification
The infrared aerial image (Figure 2) was classified into four forest cover classes namely; natural forest, Plantation Forest, and the other scattered forest (Figure 3). Sample plots were located in each of the classes.
b) Topography /Elevation
Digital Elevation Model was stratified using heights above sea level where sample points were placed within an interval of 200 m, categorizing them into high and low elevation. Low elevation falling between 2000 m to 2400 m and high elevation between 2400 m to 2800 m above sea level (Figure 4).
c) Canopy Height
Canopy Height Model was used to classify the area in to two categories using the Kenyan forest definition of forests (KFS, 2010b), vegetation below 2 meters was eliminated from the analysis. These were the areas with vegetation types such as agriculture, Grassland and short Shrubs. Figure 5 shows the categories of different canopy heights. Those plots that had an average height below 10 m and above 2 m were analyzed as one group while those with heights above 10 m as another group.
![]()
Figure 2. Aerial image used in the classification.
![]()
Figure 4. Digital Elevation Model (m), black dots represent the GPS points.
![]()
Figure 5. Canopy Heights (m), red dots represent GPS Points.
2.4. Field Data Collection
The biometric field data was manually collected using the ICFRA approved methodology (REF) for field inventories in Kenya in the period January-April 2015. A circular plot with a radius of 15 m equivalent to the one of the generated grid size of 26.5 × 26.5 m was used. The aim of field measurements was to capture (i) the actual forest heights (ii) the total amount of woody vegetation (biomass) on the sample plots. All trees within the sample plot with diameter at breast height (DBH) of at least 5 cm were measured. Parameters taken for each tallied tree were Diameter at Breast Height (DBH) and the species type. For the sample tree, which was the fifth tree additional features such as Bole height, total height, Stamp height, stamp diameter, species and the tree health, were recorded. The parameters were to aid the estimation of the forest biomass. In total, data was collected from 78 plots.
2.5. Data Processing
The LiDAR output had infrared image (Figure 6) and point cloud data. The ALS LiDAR point cloud data in las file format, 2.5 × 2.5 km blocks in the Kenyan coordinate system (Arc 1960/UTM zone 37 s), was classified as ground, noise and unclassified; heights were calculated above the reference ellipsoid. LiDAR data processing was performed using lastools (http://rapidlasso.com/lastools/). A Digital Canopy model (DCM) was generated from the first returns (Figure 7). The individual tree positions and heights were extracted from the DCM by applying watershed delineation method where the tree picks become “ponds” and the tree branches/crowns become watersheds for all the sample plots (Figure 8).
2.6. Data Analysis
2.6.1. Tree Height Estimation
Tree heights from field observation, were measured only from the sample trees while the diameters at breast heights were measured for all the counted trees in the sample plot. Lauri Mehtätalo’s lmfor-package in R software ( Mehtätalo, 2008 ) that uses the Curtis model was used to estimate unmeasured tree heights. The model used the measured heights and diameters at breast height measured for the estimation and compared the results with LiDAR data. Curtis model: h (d) = bh + a (d/(1 + d))b, Where, h = tree height d = tree diameter at breast height bh = breast height and a, b= parameters of the equation generated by fitting a linear model.
Tree heights from LiDAR data were extracted from the Canopy Height Model (CHM) using plot center coordinates with a radius of 15 m., where heights below 2 m were excluded. This was the plot radius where all measurements were taken. The extracted values were then averaged to obtain average tree height in the plot from LiDAR.
2.6.2. Above Ground Biomass (AGB) Estimation
The AGB for each sample plot was calculated using allometric equations ( Ketterings et al., 2001 ) sourced from Kinyanjui et al. (2014) who interrogated a variety of allometric equations from different sources in Kenya using dummy values for a realistic and unbiased biomass estimation.
The Above Ground Biomass (AGB) of the individual trees was estimated using field measured tree heights and the Diameter at Breast Height (DBH). The ABG for the trees was calculated as follows,
i) Indigenous trees AGB = exp(2.18435 *log10(D1.3)) − (0.20922 *log10(D1.3)) − 1.13559) (Bradley 1988).
ii) Other trees 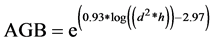 ( Chidumayo, 2012 ) (where AGB― Above Ground Biomass, D1.3―Diameter at Breast Height at 1.3 m and H― Height.
( Chidumayo, 2012 ) (where AGB― Above Ground Biomass, D1.3―Diameter at Breast Height at 1.3 m and H― Height.
The Total plot level AGB was calculated from the tree-level biomass values per hectare using R Statistical tool.
AGB using LiDAR data was also estimated using tree heights from the Canopy Height Model and plot level DBH estimated using a model generated from the measured parameters in the field data. The model used was y = 12.167x1.0621
![]()
Figure 9. Scatter plots for relationship between measured parameters of Dbh and height.
(Figure 9). The LiDAR estimated AGB was then calculated using the estimated DBH and the generated tree heights from the Canopy Model. The same models (Allometric equations) used in the estimation of AGB in the field data were used to ensure harmony of AGB estimates. The Total plot level AGB was calculated from the tree-level biomass values per hectare and were therefore compared with the estimation from field data.
2.7. Statistical Analysis
Single factor analysis of variance (ANOVA) at 95% confidence level, correlation and regression analysis were subjected to the data. Scatter plots from the relationships between the two set of variables and the difference in means were generated. The first was the relationship between tree measurements from the ground (field measurements) and trees estimated from LiDAR and the second set of variables was the biomass estimated from field measurements and that from LiDAR. The ground-based data (biometric data) was used as check for the ALS data to determine the usage of the ALS in estimating the height and biomass in absence of the ground data. The statistical analysis results were used to evaluate the accuracy based on Root Mean Square Error between the variables under different conditions namely different topographic heights, different canopy heights and different forest cover heights. The same evaluation was done under different topographic conditions to ensure that no bias in LiDAR height and AGB estimates are attributed to slope conditions in a forest.
3. Results
3.1. Tree Heights Estimation
1) Forest Types
From the best line of fit, the Coefficient of determination (R2) which describes the relationship between the predictor (field height) and predicted values (LiDAR height) was established as 0.840, 0.600, 0.899 and 0.836 for all forest types, natural forest, plantation forest and other scattered forest respectively as shown in Table 1.
The overall estimated height relationship of field measured height and LiDAR estimated height is good. However, it is noted that the plantation area has the best relationship as compared to other forest types.
2) Topography
Low elevation areas shows a very good relationship in comparison to high elevation areas (Table 2).
3) Canopy Heights
Table 3 shows a summary of the relationship results indicating a better relationship in the taller trees than the short ones.
ANOVA RESULTS:
Tables 4-6 show the results from ANOVA in different forest types, elevation and canopy heights respectively.
3.2. Above Ground Biomass Estimation
Linear relationships using the AGB results from biometric data and LiDAR data was calculated. A similar analysis to the heights comparison was done for the forest categories, differences in elevation and canopy heights. Tables 7-9 show a summary of the results.
![]()
Table 1. Summary statistics for the field height and Airborne LiDAR height (Forest types).
![]()
Table 2. Summary statistics for the field height and Airborne LiDAR height (Topography).
![]()
Table 3. Summary statistics for the field height and Airborne LiDAR height (canopy height).
![]()
Table 4. Summary of Single Factor ANOVA for LiDAR and Field measured heights (Forest types).
![]()
Table 5. Summary on Single Factor ANOVA for LiDAR and Field measured heights in Different Elevation.
![]()
Table 6. Summary of Single Factor ANOVA for LiDAR and Field measured heights in different canopy heights.
![]()
Table 7. Summary statistics for LiDAR and Field estimated AGB in different forest types.
![]()
Table 8. Summary statistics for LiDAR and Field estimated AGB in different topography.
![]()
Table 9. Summary statistics for LiDAR and Field estimated AGB in different canopy heights.
![]()
Table 10. Summary of Single Factor ANOVA for LiDAR and Field estimated AGB (Forest types).
![]()
Table 11. Summary on Single Factor ANOVA for LiDAR and Field estimated AGB in Different Elevation.
![]()
Table 12. Summary of Single Factor ANOVA for LiDAR and Field estimated AGB in different canopy heights.
A single factor ANOVA was used to evaluate the variance of the means between the estimated AGB from the estimated heights in the field and LiDAR data. The AGB underwent a similar analysis as the tree height estimates. This was to test if there are any variations in the estimation of AGB under different conditions. Tables 10-12 show a summary of the results.
4. Discussions
4.1. Tree Height Measurements
The study assumed that the heights obtained from field measurements were accurate and were used to determine the accuracy of estimated heights from LiDAR data. Several previous studies have indicated a high correlation between tree measurements derived from LiDAR and those measured from the field. However, in this study the correlation was tested under different conditions at a plot level.
The overall correlation of all the plots indicated a high correlation with a value of R2 as 0.840, RMSE of 3.350 m and correlation coefficient of 0.917. A further analysis that was conducted to check the correlation of the estimated heights under different forest types indicated that the plantation forest had the highest correlation with a correlation coefficient of 0.950, a R2 value of 0.899 with a RMSE of 2.926 m. This is in comparison with Natural forest and other forest.
The high correlation in plantation could be attributed to homogeneity in the canopy height and species types. For the natural forest, there are mixed species with different growth rate and variation in crown shape. This type of forest has complex shape at the tree-top with overlapping crown, which makes it a challenge to target the tree-top than the plantation forest ( Zhen et al., 2016 ) and may have contributed to the lower correlation as reported.
From the ANOVA results, there was a significance difference in the heights estimated in both high and low elevation areas. However, using the linear regression, low elevation areas that were generally flat showed a better correlation than the high-elevated areas. Slope and angle in the hilly (high-elevation) may have contributed this. A study conducted by ( Khosravipour et al., 2015 ), indicate that treetop displacements vary with terrain steepness. A complex slope lowers the accuracy of LiDAR in treetop detection hence the same on CHM generated.
From this study, regression analysis indicate that the height of the trees does not affect the accuracy of LiDAR though there was significance difference using ANOVA in shorter trees.
4.2. Above Ground Biomass Estimation
Field measured AGB was calculated using allometric equation for individual trees then sum of the trees gave plot AGB. DBH used in LiDAR estimation was generated using a model from actual field measurements of DBH and tree height in the field. The two results at a plot level were compared using regression analysis and ANOVA to determine whether there was any relationship or significant variation in the results obtained from both methods.
An overall comparison showed a 0.863 correlation coefficient and a R2 of 0.741 which indicated a good relationship. However, sorting by forest types gave lower correlations with a R2 of 0.692 in Plantation forest and 0.594 in the natural forest.
Relationships of measured AGB and LiDAR estimated AGB in high and low elevation show a correlation coefficient of 0.830 and 0.899, with a R2 value of 0.681 and 0.803 respectively. A further scrutiny in the canopy height difference, showed poorer relationships in forests with short trees of less than 10 m with a correlation coefficient of 0.54 and R2 of 0.27 in comparison to the canopy heights above 10 m which had R2 of 0.65 and a correlation coefficient of 0.81.
ANOVA results for all the categories show that there is a significant difference in AGB estimation among ground measurements and LiDAR measurements. The difference is attributed to the accuracy of height estimation which has been described as inaccurate in many forestry inventories ( Kinyanjui et al., 2015 ). In addition to this error was propagated into the AGB calculation for LiDAR data because the model used to estimate AGB using ALS was calibrated using ground data.
5. Conclusions and Recommendation
5.1. Conclusions
LiDAR technology offers a great capability and ability in estimating vegetation parameters that aid in estimating above ground biomass in instances where ground measurements cannot be actualized. This is critical in addressing important programs such as REDD+ and national forest inventories where data may not be available for inaccessible forests.
The study has illustrated that LiDAR measurements are more accurate in harmonious forests like even aged monocultures. This is because the tree architecture is harmonized unlike the uneven aged natural forests. It is noted that most of the forests in Kenya are uneven aged and existing in mixed stands where the trees have a variety of architectural make ups. In such conditions, LiDAR measurements have to be supplemented with ground data and the best way to use this method would be to complement it with sparse ground data collection points.
5.2. Recommendation
Use of LiDAR with high-density point cloud data would be recommended to improve the accuracy in estimation. This has been proposed world over as a method to enhance the accuracy of LiDAR data ( Chen et al., 2005 ). Secondly, the 15 m radius plot used to confirm the ground data can be tested for accuracy versus costs. A smaller plot provides information at a cheaper cost since the ground trothing team can collect the information over a shorter period. However, this should be assessed against the ability to capture more accurate information which might be realized on a bigger plot.
Finally, the availability of the GLAS data for Kenya which covers many forest blocks of Kenya and has many data points ( Kinyanjui et al., 2015 ) should be correlated to this work to find the possibility of estimating biomass on these forests covered by the GLAS data and this would reduce the cost of carrying out a national forest inventory.
Acknowledgements
This study was part of the Improving Capacity in Forest Resources Assessment in Kenya (IC-FRA) project funded by the Finnish Government. It was implemented by Kenya Forest Service (KFS) (2010), Kenya Forestry Research Institute (KEFRI), Department of Resource Surveys and Remote Sensing (DRSRS), University of Eldoret (UoE), Natural Resources Institute Finland (Luke) and (Finnish Forest Research Institute, METLA. The first author is grateful to the Jomo Kenyatta University of Agriculture and Technology for the support granted to her to carry out this research.