The Universe as a Graviton Condensate: The “Dark-Bright Conjecture” ()
1. Introduction
Recently, it has been shown that the second order Friedmann equation (SOFE) can be derived from the quantum corrected Raychaudhuri equation [1] . The latter, in turn, arises from the replacement of classical geodesics with Bohmian trajectories. The resulting quantum correction terms in the SOFE provide an interesting framework of physical interpretation for some existing problems in the notion of a relativistic, homogeneous, isotropic and spatially flat universe, namely: the nature of dark matter, “the coincidence problem”, “the smallness problem” and the beginning of the universe. While developing their reasoning, the authors assume a quantum condensate of gravitons filling our universe, described by a Gaussian wave function,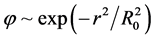 . The characteristic length scale is of the order of the Compton wavelength,
. The characteristic length scale is of the order of the Compton wavelength,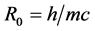 . If one identifies this length with the current size of the observable universe, one obtains
. If one identifies this length with the current size of the observable universe, one obtains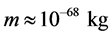 , that is the alleged mass of gravitons, in line with various theoretical and experimental bounds estimated for the same [2] [3] [4] .
, that is the alleged mass of gravitons, in line with various theoretical and experimental bounds estimated for the same [2] [3] [4] .
In the present article, we show that the previous assumption of a universe as a condensate of gravitons is consistent with a holographic Tryon’s world, and it means a universe created from quantum fluctuations of the vacuum [5] which conserves both energy and information, while also conforming the holographic principle proposed by Hooft and Susskind [6] .
2. Vacuum Fluctuations (First Postulate)
A vacuum fluctuation allows the creation of particle-antiparticle pairs of virtual particles. It can be understood as a consequence of the uncertainty principle, expressed in the form below and widely used in particle physics. According to it, energy conservation can be “virtually” violated over a lifetime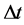 :
:
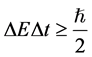 (1)
(1)
 is the net energy of the virtual particles. If one uses the mass-energy equivalence for a relativistic particle,
is the net energy of the virtual particles. If one uses the mass-energy equivalence for a relativistic particle, 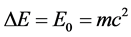 , and writes its lifetime as
, and writes its lifetime as , then one can define the rest mass in the minimum of (1), i.e. for a squeezed coherent state:
, then one can define the rest mass in the minimum of (1), i.e. for a squeezed coherent state:
 (2)
(2)
At this point, some issues should be mentioned. First of all, the approach posed at the beginning by means of the universal Compton wavelength agrees with the above definition, except for the factor 2 in the denominator. This can be explained by considering that actually a pair of particles is created, rather than one (remember that the graviton is its own antiparticle). For simplicity, we will consider only one of the gravitons created. Before proceeding we can therefore choose between two physical interpretations that lead to the same formulation: the first is that (2) acquires a physical significance from the beginning, identifying it with the quantum vacuum zero-point energy,  , with
, with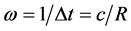 . Note that this vacuum energy corresponds to the ground state of a quantum harmonic oscillator, whose wave function is in fact Gaussian; the other option is to take (2) as a purely mathematical definition and then give it a physical meaning in the light of results.
. Note that this vacuum energy corresponds to the ground state of a quantum harmonic oscillator, whose wave function is in fact Gaussian; the other option is to take (2) as a purely mathematical definition and then give it a physical meaning in the light of results.
Secondly, (2) is in principle valid for any time during the evolution of the universe, i.e. for any
. For example, let’s suppose that immediately after the Big Bang, a particle was created and it has been stable enough to have a lifetime as long as the age of the universe. Using for the latter 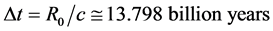 (agreed data by contemporary scientific community [7] ), one obtains
(agreed data by contemporary scientific community [7] ), one obtains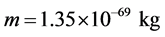 . This value particularly matches very well the graviton mass estimated in reference [2] , besides being consistent with other approaches cited above. By last, regarding the question about how a quantum fluctuation could occur in this universal scale, the arguments given by Tryon in his article are worthy of consideration [5] . On the theoretical consistency of this postulate, it should be highlighted a recent rigorous test based on the analytical solutions of the Wheeler-DeWitt equation that supports the idea of a universe spontaneously created from nothing [8] .
. This value particularly matches very well the graviton mass estimated in reference [2] , besides being consistent with other approaches cited above. By last, regarding the question about how a quantum fluctuation could occur in this universal scale, the arguments given by Tryon in his article are worthy of consideration [5] . On the theoretical consistency of this postulate, it should be highlighted a recent rigorous test based on the analytical solutions of the Wheeler-DeWitt equation that supports the idea of a universe spontaneously created from nothing [8] .
3. Totality Principle (Second Postulate)
Let’s now imagine that our virtual graviton is interacting with all the rest of the universe, whose net mass at the present time is denoted by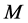 . This mass is
. This mass is
contained within the Hubble radius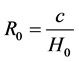 , where
, where 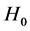 is the Hubble constant. It can be estimated using the critical density value
is the Hubble constant. It can be estimated using the critical density value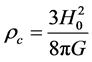 . Hence, with a little algebra, we find that the gravitational potential energy of this interaction is given by:
. Hence, with a little algebra, we find that the gravitational potential energy of this interaction is given by:
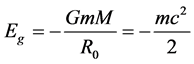 (3)
(3)
We call this postulate the “totality principle”, recalling that the whole is more than the sum of the parts and each part interacts with the whole. Given the cosmic formation of large-scale gravitationally bound structures such as galaxy groups and clusters, mainly due to the long range of gravitation in the universe, it is not unreasonable to rely on this principle.
4. Holographic Principle (Third Postulate)
Following the reasoning given by Tryon, the net energy of a universe understood as a vacuum fluctuation should be zero. Thus, although “virtually” no energy is conserved during![]() , even so there should be an additional term to override
, even so there should be an additional term to override
![]() .This is where we rely on the holographic principle, written by the following inequality:
.This is where we rely on the holographic principle, written by the following inequality:
![]() (4)
(4)
where ![]() is the Boltzmann constant,
is the Boltzmann constant, ![]() is the Planck length and
is the Planck length and ![]()
is the surface bounding a given volume of space. The principle determines that the information contained in a given volume of space can be known by the information encoded on its surface. This applied to the entire universe can be studied in depth on the works of Susskind [6] and Bekenstein [9] .
5. Conservation (Fourth Postulate)
In order to meet the energy conservation principle of the universe, we find the following equality responding to a simple mental model that will be explained below:
![]() (5)
(5)
![]() and it is what we might call a “holographic bit”. It corresponds to the upper bound in (4) using
and it is what we might call a “holographic bit”. It corresponds to the upper bound in (4) using![]() , the Planck area. It is known that this area plays an important role in black hole entropy. The surface of a spherical black hole increases in this amount when it swallows one bit of information [10] .
, the Planck area. It is known that this area plays an important role in black hole entropy. The surface of a spherical black hole increases in this amount when it swallows one bit of information [10] .
Meanwhile, ![]() , that is the temperature of Hawking radiation for a black hole whose mass is equal to
, that is the temperature of Hawking radiation for a black hole whose mass is equal to![]() , in our case the mass of the universe.
, in our case the mass of the universe.
6. Yukawa-Type Gravitational Potential (Fifth Postulate)
Finally, just as it is done by Ali and Das, we will now assume for gravity a Yukawa-type of force law, ![]() [1] . In our context, this
[1] . In our context, this
supposition makes physical sense since we are working with a non-vanishing mass for the boson associated with the gravitational interaction. But only for scopes commensurable with the radius of the universe, for which gravity has not been tested, this correction makes sense numerically speaking. Otherwise, the
exponential term is negligible, i.e.![]() . Through this Yukawa interaction for gravity, we propose the following reformulation of (5):
. Through this Yukawa interaction for gravity, we propose the following reformulation of (5):
![]() (6)
(6)
Instead (3), we now have![]() , and
, and ![]() is a cor-
is a cor-
rection factor for the information entropy (4). It should be noted that this law can be obtained not only through a quantum potential, but also through extended theories of gravity. In this sense, it is also important to stress that some unresolved cosmological issues, such as dark energy and dark matter, can in principle be approached from extended theories of gravity [11] . On entropic gravity resulting from a Yukawa type of correction to the gravitational force, there are some articles that can be studied, arriving at correction factors equivalent to the one we put forward in (6) [12] [13] .
7. Conjecture
Before stating our conjecture and only with the aim of gaining insight, it is useful to read (5) and (6) from the outlook provided by the following simple mental model: for each graviton created into the observable universe, the surface of the latter increases in a Planck area unit which, in turn, emits Hawking radiation in order to conserve the net energy of the system. This model is in agreement with a recent paper that studies the idea of information transfer between a test particle and the holographic screen in entropic gravity [14] .
In other words, from a viewpoint of information one could imagine that our universe behaves like a Schwarzschild black hole, so that the information gain of a “vacuum bit” given by the creation of the graviton (rest mass-energy or zero-point energy) is offset by the information loss of a “gravitational bit rot” (gravitational potential energy in its interaction with the rest of the universe) plus a “holographic bit rot” or “thermal bit rot”, understood as information entropy (Hawking radiation in the event horizon of our universe). It is noteworthy that using maximum entropy in (4) with minimum uncertainty in (1) is physically consistent from this perspective of information. On the other hand, it is important to note
that the area of the observable universe is composed of ![]()
Planck area units, as it follows in a study of the computational capacity of the universe [15] . The same suggests that the previous order of magnitude corresponds to the maximum number of bits of the universe, counting both the matter and conventional energy as the gravitational degrees of freedom. This in turn coincides with the maximum number of elementary logical operations that could be performed in the universe. If one multiplies this number by the graviton mass, with a little algebra one finds that![]() , whereby the quantum condensate pervading the universe may contain
, whereby the quantum condensate pervading the universe may contain ![]() gravitons. In the same sense, this is in agreement with another recent work which investigates the relation between the mass of the graviton and the number of information according to the holographic principle [16] .
gravitons. In the same sense, this is in agreement with another recent work which investigates the relation between the mass of the graviton and the number of information according to the holographic principle [16] .
Returning to reference [1] , another key point highlighted there is that the graviton mass is related in a simple way with the observed cosmological constant,
namely:![]() . Then, with this interpretation we propose the fol-
. Then, with this interpretation we propose the fol-
lowing conjecture: the energy conservation (6) of a holographic universe composed of a quantum condensate of gravitons created from nothing and interacting with everything (summary of the five postulates) is linked to well-known cosmological parameters of the ΛCDM model. It is known that the densities of dark energy ![]() (or vacuum density), dark matter
(or vacuum density), dark matter![]() , baryonic matter and neutrinos (both relativistic and non-relativistic)
, baryonic matter and neutrinos (both relativistic and non-relativistic)![]() , and the radiation density of the universe
, and the radiation density of the universe ![]() (only photons, excluding relativistic neutrinos), ideally satisfy this relationship condition for a flat universe:
(only photons, excluding relativistic neutrinos), ideally satisfy this relationship condition for a flat universe:
![]() (7)
(7)
In order to evaluate how this equality is mathematically linked to (6), we first square the latter obtaining:
![]() (8)
(8)
Then, by properly normalizing (8), dividing by ![]() and multiplying by an arbitrary density parameter
and multiplying by an arbitrary density parameter![]() , we find an equality wherein we propose the following identifications:
, we find an equality wherein we propose the following identifications:
![]() (9)
(9)
The term on the right in (7) can be identified with the analog in (8)![]() , that is the Hawking radiation that is lost outside the observable universe for a given time, according to the mental model explained above. In addition, we have identified
, that is the Hawking radiation that is lost outside the observable universe for a given time, according to the mental model explained above. In addition, we have identified ![]() with baryonic matter and neutrinos,
with baryonic matter and neutrinos, ![]() with dark matter, and the rest mass-energy term mi-
with dark matter, and the rest mass-energy term mi-
nus the pure gravitational term with dark energy. In other words, to gain perspective: the pure vacuum energy account for dark energy, the geometric mean between vacuum energy and gravitational energy account for dark matter, the pure gravitational energy account for baryonic matter and the Hawking thermal energy account for radiation in the universe. Putting in this way, one can say that the forms of mass-energy in the universe go from vacuum to matter (or “from dark to bright”), depending on the share of the gravitational energy on the total energy of the system. This is the reason why we could denominate our proposal as the “dark-bright conjecture”.
8. Results
Applying (9) for the current time (![]() ) and using
) and using ![]() for photon density, based on the best fit of Planck 2013 data (combination of the Planck temperature power spectrum with a WMAP polarization low-multipole likelihood) [17] , the values shown in the first column of Table 1 are obtained. In the second column, these predicted values are compared with the most accurate results of the Planck space mission observations for the content of the universe, relying on ΛCDM model.
for photon density, based on the best fit of Planck 2013 data (combination of the Planck temperature power spectrum with a WMAP polarization low-multipole likelihood) [17] , the values shown in the first column of Table 1 are obtained. In the second column, these predicted values are compared with the most accurate results of the Planck space mission observations for the content of the universe, relying on ΛCDM model.
On the other hand, the cosmic microwave background radiation, from the era of recombination (378,000 years after the Big Bang), studied by WMAP yields a result of 15% for the density of photons at that time [18] . With (9), the following
![]()
Table 1. Comparison for the cosmological parameters between predicted values using (9) and best fits resulting from Planck spacecraft observations.
values for the remaining cosmological densities are recovered:![]() ,
, ![]() ,
,![]() . WMAP estimations are
. WMAP estimations are ![]() for the density of neutrinos and atoms,
for the density of neutrinos and atoms, ![]() for dark matter, and negligible dark energy at that epoch. Regarding the latter our model predicts that
for dark matter, and negligible dark energy at that epoch. Regarding the latter our model predicts that![]() . This discrepancy could either give a new perspective to the content of dark energy in the early universe, or may give some hint to a recent conjecture about the possible conversion of dark energy to dark matter during the evolution of the universe [19] , which is beyond the scope of this work. Within the perspective of future work, new results will be sought to support our conjecture.
. This discrepancy could either give a new perspective to the content of dark energy in the early universe, or may give some hint to a recent conjecture about the possible conversion of dark energy to dark matter during the evolution of the universe [19] , which is beyond the scope of this work. Within the perspective of future work, new results will be sought to support our conjecture.
9. Conclusion
In summary, we have shown that the assumption of the universe as composed of a quantum condensate of gravitons is consistent with the idea of a holographic universe created from vacuum fluctuations that conserves the total energy. Using for gravity a Yukawa-type force law, we have proposed a simple heuristic conjecture that links the net energy conservation of the system with the cosmological parameters of the universe within the ΛCDM model, describing the contents of the universe. Our “dark-bright conjecture” not only can provide a physical framework to explain both the “coincidence problem” as the nature of dark matter, but it is also capable to predict theoretical values for the cosmological parameters that are in great agreement with recent astronomical observations.
Acknowledgements
I thank my daughter Vera, who, still in the mother’s belly, has inspired me the idea behind this article. I am grateful also with I. Berdakin, G. Lener, D. Barraco, G. Dotti, R.J. Gleyser and V. Rodríguez for their useful comments.