Transient Stability Study of Power System with Large-Scale Wind Farm Integration ()
1. Introduction
With the continuous development of China’s modernization, renewable energy power generation will become the main power generation technology in the future, in which the wind power in renewable energy accounts for a large proportion. In recent years, China’s wind power is centralized and large-scale tendency. The large scale grid connected wind power system has changed the original structure and characteristics of the system, so it is necessary to study the transient stability of the power system connected with the wind power, and put forward the control strategy to improve the transient characteristics of the system. The current research on the transient stability of power system with wind farm containing mainly based on equivalent model of wind farm, and through the simulation experiment results [1] [2] [3] [4] [5]. The literature [1] through the simulation of wind farm access point near the fault will reduce the system transient stability and when the fault occurs near the synchronous generator, wind power access has a positive impact on the transient stability of the system. The literature [3] found in doubly fed wind power generator system with little access to the same capacity and synchronous machine simulation, better transient stability characteristics of DFIG. The literature [4] proposed wind power on the influence of system transient stability depends on the fan access for the disturbance of cluster and the remaining cluster inertia, mechanical power and electromagnetic power influence. Although the above conclusions have been obtained through the fan modeling and simulation, but the lack of rigorous theoretical support, it cannot be a good mechanism to illustrate the impact of wind power grid on the transient stability of the system. In the wind power system transient control strategy, most of the literature is also concluded by simulation, lack of theoretical proof [11] [12] [13] [14]. Based on EEAC, this paper makes study on transient stability analysis and stability calculation of wind power system. And proposes a theory about the way to analyse and calculate transient stability of the power system with wind farm.
2. Study on Transient Characteristics of Wind Power Integration Based on EEAC
2.1. EEAC on the Power System with Wind Farm
In this paper, based on EEAC, the transient stability analysis of power system with wind farm is studied. Firstly, the system model is described. We use the classical two order model to describe a generator, ignore the dynamics of prime mover and governor, ignore the dynamics of excitation system [6] [7]. The network and load is linear and the network contractes to generator node. In this paper, the center of inertia (COI) coordinate system is discussed. After the system suffers from a simple fault, we assume that the system is unstable mode for dual mode. Assuming that the dominant UEP or unstable modes are known, the S cluster is the most serious one, and the other is A cluster. And it is assumed that there is no relative oscillation between the rotor angles of the S cluster and the A cluster. The system is equivalent to two computers, and the dual system is equivalent to a single-machine infinite-bus system. The equation of motion [8] is shown in Equation (1):
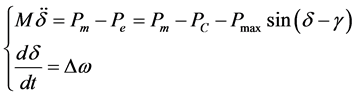 (1)
(1)
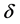 is the equivalent single rotor angle.
is the equivalent single rotor angle. 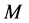 is the equivalent single machine inertia time constant.
is the equivalent single machine inertia time constant. 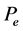 is the electromagnetic power and
is the electromagnetic power and 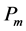 is mechanical power:
is mechanical power:
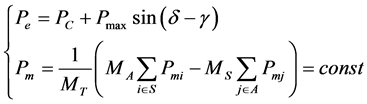 (2)
(2)
And:
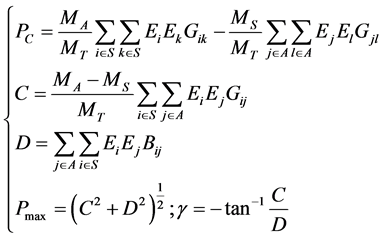 (3)
(3)
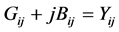 is the element of nodal admittance matrix.
is the element of nodal admittance matrix. 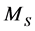 and
and 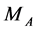 is the Inertia time constant of the S cluster and the A cluster,
is the Inertia time constant of the S cluster and the A cluster,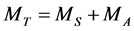 .
.
The transient stability of the system without wind farms is analyzed using EEAC. Next, the wind power system is discussed. We discuss about wind farms based on double-fed Induction generator controlled by modern power electronics technology. Because the wind farm based on asynchronous generator does not consider its own power angle stability, its influence on the transient stability of power system is mainly reflected in the power angle stability of synchronous generator [9] [10]. We suppose that the injection current of the wind farm is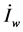 , and power of the wind farm is
, and power of the wind farm is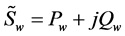 . Assume that the network has shrunk to only the generator nodes and wind farm grid nodes. Due to the S cluster is a serious disturbance in the dual-system, the wind farm is integrated into the S cluster by considering the most harmful situation. The cluster of the system is shown in Figure 1. The node of wind farm grid is w, and S cluster node is i. Mutual admittance between w and i is
. Assume that the network has shrunk to only the generator nodes and wind farm grid nodes. Due to the S cluster is a serious disturbance in the dual-system, the wind farm is integrated into the S cluster by considering the most harmful situation. The cluster of the system is shown in Figure 1. The node of wind farm grid is w, and S cluster node is i. Mutual admittance between w and i is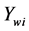 . And it is much more than
. And it is much more than 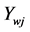 which is the Mutual admittance between w and j. And j is the A cluster node. Further, we assume
which is the Mutual admittance between w and j. And j is the A cluster node. Further, we assume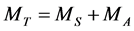 .
.
The nodal admittance matrix of the power system with wind farms can be expressed as
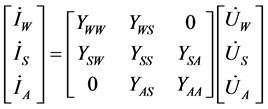 (4)
(4)
From (3) we can get:
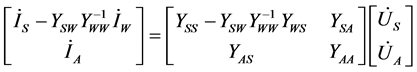 (5)
(5)
Or:
![]() (6)
(6)
The injected current on the node i of the S cluster is:
![]() (7)
(7)
![]() is current displacement coefficient.
is current displacement coefficient.
The increase of current on the node of the S cluster can be converted to the change of the self admittance of the S cluster in the admittance matrix
![]() (8)
(8)
So, the expression of ![]() and
and ![]() is:
is:
![]() (9)
(9)
Because of the change of self admittance of S cluster, according to Formula (3), ![]() and
and ![]() do not change. So
do not change. So ![]() and
and ![]() do not change, too. However,
do not change, too. However, ![]() becomes:
becomes:
![]() (10)
(10)
In this formula, ![]() is a coefficient which means the degree of contact between wind farm and system. The increment of
is a coefficient which means the degree of contact between wind farm and system. The increment of ![]() is:
is:
![]() (11)
(11)
At the same time, considering the mechanical power of the wind farm:
![]() (12)
(12)
Therefore the total mechanical power of the system is:
![]() (13)
(13)
In formula (11), ![]() is the mechanical power of thermal power unit, and in the transient process, it is assumed that the constant.
is the mechanical power of thermal power unit, and in the transient process, it is assumed that the constant. ![]() is the mechanical power of the wind farm.
is the mechanical power of the wind farm.
To sum up, considering the wind farm access, formula (1) should be written as:
![]() (14)
(14)
Then the acceleration area and deceleration area are calculated according to the transient power angle characteristic curve. The transient power angle characteristic curve of wind power is shown in Figure 2. We assume the power angle characteristics of the system before fault is![]() , and
, and ![]() during fault,
during fault, ![]() after fault.
after fault.
![]() (15)
(15)
Formula (13) shows the mechanical power of the system. ![]() is invariable.
is invariable. ![]() related to the mechanical power of each wind turbine. Assuming it is
related to the mechanical power of each wind turbine. Assuming it is ![]() when it is running normally, and
when it is running normally, and ![]() when it is in the transient process. Due to the wind turbine has a certain degree of regulation of mechanical power,
when it is in the transient process. Due to the wind turbine has a certain degree of regulation of mechanical power, ![]() will reduced to a certain extent during the fault period, and recover after the fault. Therefore, the change of the mechanical power of the wind power system
will reduced to a certain extent during the fault period, and recover after the fault. Therefore, the change of the mechanical power of the wind power system ![]() is shown in Figure 2.
is shown in Figure 2.
The power angle characteristics of the system are different under different operating conditions. Parameters like![]() ,
, ![]() ,
, ![]() and
and![]() ,
, ![]() can be calculated according to Formula (3), Formula (9) and Formula (10) and corresponding node admittance matrix parameters.
can be calculated according to Formula (3), Formula (9) and Formula (10) and corresponding node admittance matrix parameters.
The stable equilibrium point of the system is derived:
![]() (16)
(16)
After the system failure, the stable equilibrium point and unstable equilibrium point:
![]() (17)
(17)
According to Formula (15), we can get stable equilibrium point after failure ![]() and unstable equilibrium point after failure
and unstable equilibrium point after failure![]() .
.
After getting the above work points, according to the fault removal time and the high order Taylor series method, we can get ![]() [8]. System acceleration area and maximum deceleration area:
[8]. System acceleration area and maximum deceleration area:
![]() (18)
(18)
According to the transient acceleration area ![]() and maximum deceleration area
and maximum deceleration area![]() , we can get the transient stability of the system:
, we can get the transient stability of the system:
![]() (19)
(19)
2.2. Simulation of the Analysis Method of the Power System with Wind Farm Based on EEAC
In this part, the transient stability analysis method proposed in 2.1 of wind power system is verified. Based on the above analysis, we make a transient calculation on a certain system and then we make a simulation of the system based on PSASP. The calculated results are compared with the simulation results to judge the correctness of theoretical analysis and evaluate the accuracy of theoretical calculation.
The system is shown in Figure 3.
The fault condition is: three phase grounding short circuit occurs at the first end of AC line when the simulation time is 1.0 second and the fault last for 0.1 second. It can be seen from the simulation experiment that generator1 is among S cluster, and generator 0 is among A cluster.
The nodal admittance matrix can be obtained according to the equivalent network of wind power system, and it is shown as:
![]() (20)
(20)
Through the network transformation we can get:
![]() (21)
(21)
The influence of the wind power is regarded as generator1 to increase the injection current. Further, the increase of the injection current of generator 1 can
be regarded as the change of generator1’s self admittance. In this way we can propose that the influence of the wind power can be regarded as the change of generator1’s self admittance. The nodal admittance matrix can be further written as:
![]() (22)
(22)
![]() is the change of generator 1’s self admittance and it can be calculated using admittance matrix parameters. Further, by calculating the ground admittance, we can get the equivalent resistance and reactance, therefore, can the wind effect of electric field on the system is equivalent to a parallel negative resistance and negative reactance.
is the change of generator 1’s self admittance and it can be calculated using admittance matrix parameters. Further, by calculating the ground admittance, we can get the equivalent resistance and reactance, therefore, can the wind effect of electric field on the system is equivalent to a parallel negative resistance and negative reactance.
Calculate the system shown in Figure 3, we found that before the fault the wind farm is equivalent to a negative resistance, and during the fault and a short time after fault clearing the wind farm is equivalent to a parallel negative resistance and negative reactance. And the transient process of wind power system is calculated according to the influence of resistance and reactance in parallel. The calculation results and simulation results can be seen as Table 1.
It can be seen from the Table 1 that the maximum difference of the theoretical calculation results and simulation results is 3.8 degrees in the first swing range of transient power angle stability curve. So, we can come to conclusion that the theoretical analysis method of the power system with wind farms is correct for a simple system. As for multicomputer systems, we can turn them into simple systems based on EEAC.
3. Analysis of Wind Power System Transient Stability Control Strategy
Based on the above analysis of the transient stability of power system with wind farm, we found that we can change the system transient acceleration area and deceleration area by changing ![]() and
and![]() . In this part, the transient stability of wind power system with SVG reactive power compensation equipment is analyzed. And finally, the simulation experiment is carried out.
. In this part, the transient stability of wind power system with SVG reactive power compensation equipment is analyzed. And finally, the simulation experiment is carried out.
SVG can play a role in maintaining the transient process of the stroke and grid voltage level [15]. We can found from Formula (9) that by providing reactive
![]()
Table 1. Calculation results and simulation results.
power support, SVG can improve the genertor output voltage, reduce the degree of electromagnetic power reduction, and the acceleration area can be reduced and the deceleration area is increased, so as to improve the transient stability of the system and improve the transient stability of the system.
The simulation experiment bases on WSCC 3 machine 9 node system. The system is shown in Figure 4.
G1, G2, G4 are synchronous generators, and wind farm is a doubly-fed wind turbine. We conducted two sets of experiments. Experiment 1: Set SVG in Wind farm grid bus; Experiment 2: Do not set SVG in Wind farm grid bus, and other conditions are consistent with experiment 1. Fault condition: a three-phase short-circuit fault occurs in the 55% the between GEN3-230 bus and STNB-230 bus. Fault lasts for 0.25 seconds and we observe the swing of power angle between synchronous generators in transient state. The experimental test curves are shown in Figure 5.
From Figure 5, we will find that Experiment1 that using SVG to make reactive power compensation during that fault has smaller power angles wing, compared with Experiment 2 that do not use SVG. The experimental results show that SVG can improve the transient stability of power system by using reactive power compensation, further, it is proved that the proposed control strategy is effective.
4. Conclusions
This paper proposed a method of analysis and calculation for transient acceleration area and deceleration area in wind power system. Than a simulation experiment was carried out to verify the correctness of the theory. By comparing the simulation results and calculation results, we find that the way to analyse and calculate the wind power system is correct.
On this basis, this paper proposed that using SVG to make reactive power compensation during that fault has positive impact on power system transient characteristics. And the simulation results show the feasibility of the theory.