Studying the Nuclear Structure of Some Target Nuclei Used for Radiotherapy Nuclei Production by Using Skyrme-Hartree-Fock Method ()
1. Introduction
Radionuclides find applications in many fields. Their major use is in medicine, in both diagnosis and therapy. The production of radionuclides is carried out by using nuclear reactors. The reactor produced radionuclides are generally neutron excess nuclides [1] . Radioisotopes are essential for a variety of applications in medicine as diagnosis by scintigraphy and treatment of various diseases by internal radiotherapy. There is a rapid growth in the use of radionuclides for treatment of cancer in nuclear medicine paralleled by an increase of the diversity of the used radioisotopes [2] . The recent revival of interest on radionuclide therapy or targeted radiotherapy (TR) is a consequence of improvements in tissue specific biomolecules (monoclonal antibodies (mAbs), bone seeking bisphosphonates, etc.) and its potential advantages over external radiotherapy, particularly for patients with inoperable or multi-site disease as neuroendocrine tumors and disseminated bone metastases. In benign disorders TR provides an alternative to surgery or medical treatments and in cancer treatment combines target selectivity with that of being systemic [3] .
The present work is meant to investigate the applicability of the Skyrme- Hartree-Fock method (SHF) method to the descriptions and calculations of the nuclear structure for medical applications. This work is to check whether the theoretical results obtainable by the SHF method for such nuclei will turn out to be conformant with the corresponding experimental data. For this purpose we have selected a number of target nuclides, namely: 32S, 58Ni, 89Y, 90Zr, 100Mo and 197Au for production therapeutic radionuclides; 32P, 58Co, 89Sr, 90Y, 99Mo and 197Pt. The proton, neutron, mass, and charge densities with their associated root mean square (rms) radii, nuclear binding energy (BE), initial exciton numbers and the nucleon-nucleon interaction cross section will be calculated. The initial exciton numbers give the ability to investigate the neutron and proton induced reaction cross-section for these target nuclei using geometry dependent hybrid model (GDHM) for pre-equilibrium nuclear reactions. The calculated results will be compared with available experimental data.
2. Theory and Methodology
The central assumption of the Hartree-Fock (HF) approach is that the structure properties of a system, in this case nuclei, can be understood in terms of the force felt by each nucleon moving independently in an average potential or mean field (MF). This leads to the ansatz for the HF approximation that the ground-state trial wave function of a nucleus containing A nucleons is written as a Slater determinant, or antisymmetrised product of occupied states. This Slater determinant Equation (1) is built from a complete orthonormal set of single-particle wave functions (the HF basis), 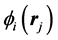 , where
, where  denotes all the spatial, spin and isospin coordinates of the jth nucleon
denotes all the spatial, spin and isospin coordinates of the jth nucleon
 (1)
(1)
HF approximation is a microscopic model that describe the structure of the nucleus in terms of the degrees of freedom of its microscopic constituents (the nucleons). In HF calculations, the most widely used interaction is the forces of Skyrme type. The definition of the Skyrme interaction can be written as the sum of two- and three-body parts [4] ,
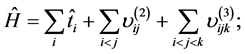 (2)
(2)
the two body part was given by
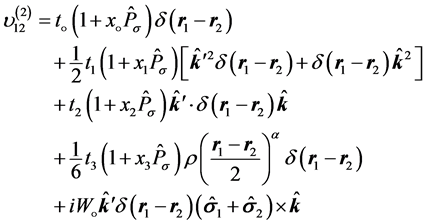 (3)
(3)
and the three-body part by
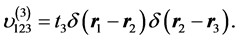 (4)
(4)
where the 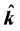 and
and 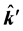 are relative momentum operators defined as
are relative momentum operators defined as
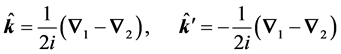 (5)
(5)
which operate on the wave functions to the right and to the left.
The Skyrem force contains six parameters as ,
, 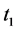 ,
, 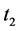 ,
, 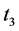 ,
, 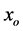 and
and 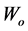 which are usually determined by fitting the experimental ground state properties of a finite nuclei within HF calculation. The expectation value of total energy of a given nucleus in a Slater determinant
which are usually determined by fitting the experimental ground state properties of a finite nuclei within HF calculation. The expectation value of total energy of a given nucleus in a Slater determinant 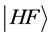 is given by [4] [5]
is given by [4] [5]
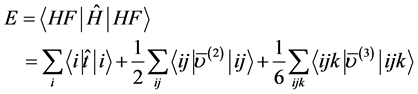 (6)
(6)
where the notation 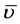 represents an antisymmetrized matrix element.
represents an antisymmetrized matrix element.
In particular, according to the SHF method, the total binding energy of a nucleus is obtained self-consistently from the energy functional [5] [6] [7] :
![]() (7)
(7)
where the kinetic energy is given by:
![]() (8)
(8)
where![]() , the energy functional of the Skyrme force and given by
, the energy functional of the Skyrme force and given by
![]() (9)
(9)
and![]() .
. ![]() is the local densities for protons and neutrons (depending on the value of q),
is the local densities for protons and neutrons (depending on the value of q), ![]() the total density,
the total density, ![]() is the kinetic energy densities for protons and neutrons and
is the kinetic energy densities for protons and neutrons and ![]() is the spin-orbit current density, that are given by
is the spin-orbit current density, that are given by
![]() (10)
(10)
The ![]() are the single-particle wave functions and
are the single-particle wave functions and ![]() the occupation probabilities calculated taking the residual pairing interaction into account. The parameters
the occupation probabilities calculated taking the residual pairing interaction into account. The parameters ![]() and
and ![]() used in
used in ![]() equation were chosen to give a compact formulation of the energy functional, the corresponding MF Hamiltonian and residual interaction [7] [8] . They are related to the more commonly used Skyrme force parameters
equation were chosen to give a compact formulation of the energy functional, the corresponding MF Hamiltonian and residual interaction [7] [8] . They are related to the more commonly used Skyrme force parameters ![]() and
and ![]() by
by
![]() (11)
(11)
The Coulomb interaction is a well-known piece of the nuclear interaction. However, its infinite range makes it very time consuming to evaluate the exchange part exactly, and it is unwise to spend most of the computing time on a small contribution. Therefore the Coulomb-exchange part is treated in the Slater approximation, and we obtain for the Coulomb energy ![]() [6] [8]
[6] [8]
![]() (12)
(12)
![]() (13)
(13)
The Coulomb part of the energy functional depends only on the charge density of the nucleus, however in many cases an approximation is made that replaces the charge density with the proton density.
In SHF method, the neutron or proton densities are given by:
![]() (14)
(14)
where ![]() is the single-particle wave function given by of state
is the single-particle wave function given by of state![]() ; the occupation probability of state
; the occupation probability of state ![]() is denoted by
is denoted by![]() . The densities in spherical representation are given by [9]
. The densities in spherical representation are given by [9]
![]() (15)
(15)
where ![]() is the harmonic oscillator radial part wave function given by the following equation [10]
is the harmonic oscillator radial part wave function given by the following equation [10]
![]() (16)
(16)
and ![]() is the associated Laguerre polynomial. The parameter b is
is the associated Laguerre polynomial. The parameter b is
called the oscillator length. It characterizes the width of the oscillator potential and is given by
![]() (17)
(17)
The rms radii of neutron and proton densities can be evaluated using Equation (15) and the following formula:
![]() (18)
(18)
The HF equations and pairing equations are derived from the total energy functional of the nucleus,
![]() (19)
(19)
where E is the total energy of the nucleus, ![]() is the energy of the Skyrme interaction,
is the energy of the Skyrme interaction, ![]() is the Coulomb interaction energy,
is the Coulomb interaction energy, ![]() is the two- nucleon interaction pairing energy, and Ec.m is the correction for the spurious center-of-mass motion of the mean field [6] .
is the two- nucleon interaction pairing energy, and Ec.m is the correction for the spurious center-of-mass motion of the mean field [6] .
The initial exciton numbers (![]() , where p and h are the numbers of excited particles above the Fermi energy and below it, respectively) are very important in pre-compound or pre-equilibrium (PEQ) nuclear reactions. Nucleon induced reactions are assumed in the hybrid (HM) and the geometry-dependent hybrid (GDH) models [11] [12] to begin with the excitation by the projectile of a two-particle―one-hole (2p1h) doorway configuration. Where in each scattering, some nucleons may be unbound. These nucleons may either be emitted into the continuum or may rescatter. Because the possibilities of scattering are much greater than the possibilities for annihilation, the equilibration cascade may be formulated in a “never come back” approximation, i.e., in each step, each nucleon makes a two-body collision creating an additional particle-hole pair. The interactions between nucleons or the free scattering cross-sections of differing isospin projections are approximately three times that of nucleons of the same isospin projections. So
, where p and h are the numbers of excited particles above the Fermi energy and below it, respectively) are very important in pre-compound or pre-equilibrium (PEQ) nuclear reactions. Nucleon induced reactions are assumed in the hybrid (HM) and the geometry-dependent hybrid (GDH) models [11] [12] to begin with the excitation by the projectile of a two-particle―one-hole (2p1h) doorway configuration. Where in each scattering, some nucleons may be unbound. These nucleons may either be emitted into the continuum or may rescatter. Because the possibilities of scattering are much greater than the possibilities for annihilation, the equilibration cascade may be formulated in a “never come back” approximation, i.e., in each step, each nucleon makes a two-body collision creating an additional particle-hole pair. The interactions between nucleons or the free scattering cross-sections of differing isospin projections are approximately three times that of nucleons of the same isospin projections. So ![]() over the energy range of interest for the PEQ decay calculations under consideration [13] . The GDH model takes into account the density distribution of the nucleus, and it takes the initial exciton number as
over the energy range of interest for the PEQ decay calculations under consideration [13] . The GDH model takes into account the density distribution of the nucleus, and it takes the initial exciton number as ![]() (1 neutron, 1 proton and 1 hole) [14] . The initial neutron and proton exciton numbers, for each partial wave can be evaluated for a neutron and proton induced reaction on a target as [15]
(1 neutron, 1 proton and 1 hole) [14] . The initial neutron and proton exciton numbers, for each partial wave can be evaluated for a neutron and proton induced reaction on a target as [15]
![]() (20)
(20)
![]() (21)
(21)
where ![]() and l is the orbital angular momentum. The radius of the 1thentrance channel partial wave is given by
and l is the orbital angular momentum. The radius of the 1thentrance channel partial wave is given by ![]() where
where![]() , is the reduced de Broglie wavelength of the projectile. Tel et al. [16] suggested that for nucleon-induced reaction cross-sections, the neutron and protons impact parameters
, is the reduced de Broglie wavelength of the projectile. Tel et al. [16] suggested that for nucleon-induced reaction cross-sections, the neutron and protons impact parameters ![]() and
and ![]() in Equations (20) and (21) can be replaced with the neutron density
in Equations (20) and (21) can be replaced with the neutron density ![]() and the proton density
and the proton density ![]() distributions from the values calculated by taking into accounts ingle-particle wave functions with Equation (15). So, the initial neutron and proton exciton numbers can be evaluated from their densities using Skyrme nucleon-nucleon effective interaction in the nucleon-induced pre-compound reactions.
distributions from the values calculated by taking into accounts ingle-particle wave functions with Equation (15). So, the initial neutron and proton exciton numbers can be evaluated from their densities using Skyrme nucleon-nucleon effective interaction in the nucleon-induced pre-compound reactions.
The absolute emission spectral yields of the proton and neutron in (n, p) and (p, n) reactions prior to the attainment of statistical equilibrium can evaluated using HM and GDH. The HM for pre-equilibrium decay can be written as
![]() (22)
(22)
![]() (23)
(23)
where ![]() is the reaction cross-section,
is the reaction cross-section, ![]() is level density for single particle of type q (proton or neutron),
is level density for single particle of type q (proton or neutron), ![]() is the equilibrium (most probable) particle plus hole (exciton) number,
is the equilibrium (most probable) particle plus hole (exciton) number, ![]() the initial exciton number,
the initial exciton number, ![]() is the number of particle type
is the number of particle type ![]() in
in ![]() exciton hierarchy,
exciton hierarchy, ![]() represents number of particles of the type
represents number of particles of the type ![]() emitted into the unbound continuum with energy channel between ε and
emitted into the unbound continuum with energy channel between ε and![]() . The term in the first set of square brackets of Equation (23) represents the number of particles to be found (per MeV) at a given energy ε for all scattering processes leading to an “n” exciton configuration.
. The term in the first set of square brackets of Equation (23) represents the number of particles to be found (per MeV) at a given energy ε for all scattering processes leading to an “n” exciton configuration. ![]() is emission rate of a particle into the continuum with channel energy ε and
is emission rate of a particle into the continuum with channel energy ε and ![]() is the intranuclear transition rate of a particle. The second set of square brackets in Equation (23) represents the fraction of the q type particles at an energy which should undergo emission into the continuum, rather than making an intranuclear transition. The
is the intranuclear transition rate of a particle. The second set of square brackets in Equation (23) represents the fraction of the q type particles at an energy which should undergo emission into the continuum, rather than making an intranuclear transition. The ![]() represents the average fraction of the initial population surviving to the exciton number being treated. U is the residual nucleus excitation energy, E is the composite system excitation energy (
represents the average fraction of the initial population surviving to the exciton number being treated. U is the residual nucleus excitation energy, E is the composite system excitation energy (![]() , where the
, where the ![]() is the particle binding energy), and
is the particle binding energy), and ![]() is the number of ways. It has been demonstrated that the nucleon-nucleon scattering energy partition function
is the number of ways. It has been demonstrated that the nucleon-nucleon scattering energy partition function ![]() is identical to the exciton state density
is identical to the exciton state density![]() , and may be derived by the certain conditions on nucleon-nucleon scattering cross-sections. The nucleus has a density distribution which can affect PE decay in two ways. The first way is related to the nucleon mean free path which is expected to be longer in the diffuse nuclear surface. Secondly, in a local density approximation, there is a limit to the hole depth. These two changes were incorporated into GDH model. The differential emission spectrum is given in the GDH model as [16] [17]
, and may be derived by the certain conditions on nucleon-nucleon scattering cross-sections. The nucleus has a density distribution which can affect PE decay in two ways. The first way is related to the nucleon mean free path which is expected to be longer in the diffuse nuclear surface. Secondly, in a local density approximation, there is a limit to the hole depth. These two changes were incorporated into GDH model. The differential emission spectrum is given in the GDH model as [16] [17]
![]() (24)
(24)
where ![]() is the reduced de Broglie wavelength of the projectile and
is the reduced de Broglie wavelength of the projectile and ![]() is the transmission coefficient for
is the transmission coefficient for ![]() partial wave. The GDH model is made according to incoming orbital angular momentum in order to account for the effects of the nuclear-density distribution.
partial wave. The GDH model is made according to incoming orbital angular momentum in order to account for the effects of the nuclear-density distribution.
3. Results and Discussion
In the present work, the calculated nuclear density profiles have been calculated using SHF with SkM parameterization. This parameterization was chosen in the light of the discussion on the rms charge density radii. The density at the center of an atomic nucleus decreases slightly with increasing mass. This means that as the mass number increases of each nucleus the central density undergoes a slight diffusion and becomes less dense with increasing radius and volume [18] . The charge density distributions were obtained by folding the charge distributions of a proton with the proton density calculated with the HO wave functions
![]() where 0.8 fm is the rms charge radius of a proton
where 0.8 fm is the rms charge radius of a proton
[8] . In computing the observable charge densities using the SHF method, another fact should also be considered that the nucleons themselves have intrinsic electromagnetic structure. Thus, one has to compute the proton, neutron, and mass densities with the intrinsic charge density of the nucleons. To illustrate the behavior of one particle nuclear density distribution, the calculated charge, proton, neutron and mass densities of the target nuclei listed it Table 1 are depicted separately in Figure 1. Different colors are used for distinguishing between the various nuclear densities of each nucleus.
In general point of view, we can deduce that in the case of heavy nuclei, the nuclear density is constant near the center and falls fairly rapidly to zero at the nuclear surface. Their neighbors, so that, when one adds a new particle to the system, most of the others are not directly affected by its presence. Thus, interior density dose not substantially change by increasing the number of nucleons A.
![]()
Table 1. The target nuclei used for production the therapeutic radionuclide.
![]()
Figure 1. The comparison of calculated neutron, proton, charge and mass densities of the selected target nuclei using SkM parameterization.
Also, it is obvious that the central nuclear charge densities gradually decrease as the nucleons number A increases this is due to the charge in the self-consistent HF potential coming from the additional nucleons. This change in charge density is available in the interior and the surface regions of the nuclei. The contribution of additional nucleons to the density is directly associated to the orbits that are filled. These orbits are changing the densities in the interior and the surface regions.
The theoretical charge rms radii of the selected target nuclei have been calculated using various Skyrme parameterizations; SkM [19] , S1 [20] , S3 [21] , SkM* [22] and T3 [23] and given in Table 2 along with experimental data for those nuclei where it exists [24] . The agreement with experiment is seen to be very good especially with Skyrme parameterization. The results are also displayed graphically in Figure 2.
In the light of the discussion on the rms charge density radii results, the BE, proton, neutron rms radii and neutron skin thickness ![]() for the selected target nuclei have been calculated using SkM parameterization and listed in Table 3. Inspection of these data reveals that there is a good agreement with
for the selected target nuclei have been calculated using SkM parameterization and listed in Table 3. Inspection of these data reveals that there is a good agreement with
![]()
Table 2. The calculated rms charge radii (in fm) using the SHF method compared with experimental data taken from Ref. [24] .
![]()
Table 3. The rms charge radii, neutron skin thickness (in fm) and binding energies of selected target nuclei using the SHF (in MeV).
![]()
Figure 2. Rms charge radii for selected target nuclei calculated using various Skyrme parameterizations along with experimental data taken from Ref. [24] .
the available experimental data. The binding energies seem, in general to be better reproduced than the rms radii. Regarding to the neutron skin thickness, it is clear that as the mass number of the nuclei increases, the neutron density distribution becomes more extended, but this concerns the proton densities to a smaller extent. This leads to the formation of a neutron skin in elements featuring a high neutron excess.
The initial neutron and proton exciton numbers have been calculated using Equations (20) and (21) and illustrated in Figure 3. Figure 3(a) shows the initial exciton numbers for 32S. It can be noticed that the neutron exciton numbers are approximately 0.5187 times greater than the proton exciton numbers in the range from 0 to 4.4 fm beyond this range the deference gradually decreases. The
![]()
Figure 3. The calculated density-dependent initial neutron (read line) and proton (blue line) exciton numbers for (a) 32S, (b) 58Ni, (c) 89Y, (d) 90Zr, (e) 100Mo and (f) 197Au using SkM parameterization.
initial exciton numbers for 58Ni is given in Figure 3(b) the predicted exciton numbers are approximately the same and there is only a small difference in the range of 0 to 0.52 fm. In Figure 3(c) and Figure 3(d) we illustrate the initial exciton numbers of the proton and neutron for 89Y and 90Zr, they are approximately the same and the difference is in the range of 0 to 0.54 fm. Beyond 6 fm the difference gradually increases. This behavior can be attributed to the small difference between the neutron and proton numbers in these nuclei. For the rest selected target nuclei 100Mo and 197Au. The calculated initial proton and neutron exciton numbers are shown in Figure 3(e) and Figure 3(f). The HM calculations predict the maximum difference in initial neutron exciton number at approximately 0.62 fm for region up to 6 fm. After this region, the difference increases with increasing the nucleus radius. This difference can be attributed to increase the ratio of N/Z for these target nuclei. However; they predict the initial proton exciton number to be the minimum in this region. The initial proton and neutron exciton numbers have local minimum and maximum values, respectively.
The differential cross-sections of the investigated reactions have been calculated using the pre-compound code [25] illustrated in Figures 4-11. A comparison with data retrieved from the online EXFOR library is also made. The calculated proton emission spectra of 32S(n, p)32P reaction is shown in Figure 4 as a function of proton energy. The obtained results for the emission spectrum using HM with the density dependent initial exciton numbers is in a good agreement with the experimental result especially in low energy region. The calculated proton emission spectrum of 58Ni(n, p)58Co reaction is shown in Figure 5 along with the experimental data taken from Ref. [26] . As seen from figure, the maximum emission spectra of the experimental data are obtained in the range of 2.5 - 4 MeV and overestimate the theoretical spectrum using HM and the direction deceases gradually with increasing energy. The calculated proton emission spectra of 89Y(n, p)89Sr are plotted in Figure 6 as a function of energy. Generally, the proton emission spectrum using HM is over estimate the experimental data. Large discrepancy in the cross-section is observed up to 4 MeV between experimental
![]()
Figure 4. The comparison of proton emission spectra of 32S (n, p) reaction at 14 MeV neutron energy. Experimental values were taken from Ref. [26] .
![]()
Figure 5. The comparison of proton emission spectra of 58Ni (n, p) reaction. Experimental values were taken from Ref. [27] .
![]()
Figure 6. The comparison of proton emission spectra of 89Y (n, p) reaction at 14.6 MeV neutron energy. Experimental values were taken from Ref. [28] .
values and HM calculation. After 4 MeV, there is an acceptable agreement with the experimental result. The proton emission spectrum using HM calculation together with the available experimental data for 90Zr(n, p)90Y reaction are plotted in Figure 7. The prediction of HM and the experimental results are in relatively good agreement with each other. Moreover, the HM results give highest results for the low energy region up to 4 MeV and even the size discrepancies decrease grossly as proton energy increases. Figure 8 shows the emission spectrum of neutrons for 100Mo(n, 2n)99Mo reaction treated by HM. The result showed reasonable agreement with experimental data except for low and high
![]()
Figure 7. The comparison of proton emission spectra of 90Zr (n, p) reaction. Experimental values were taken from Ref. [28] .
![]()
Figure 8. The comparison of neutron emission spectra of 100Mo (n, 2n) reaction at 12 MeV neutron energy. Experimental values were taken from Ref. [29] .
energy regions where the calculated result is somewhat low. Whether this discrepancy is meaningful and conclusion with the uncertainties of the calculation is yet an open question. The neutron emission spectra produced by 100Mo(p, n)100Tu reaction was illustrated in Figure 9. The experimental data and HM result give quite similar spectra within energy range from 10 - 25 MeV. On the other hand, the experimental spectrum gives the highest result than HM calculation in about neutron energy 6 - 9 MeV. The comparison of calculated proton emission spectrum of 197Au(n, p)197Pt reaction with the experimental data is presented in Figure 10. The HM succeed to reproduced the proton emission
![]()
Figure 9. The comparison of neutron emission spectra of 100Mo (p, n) reaction Experimental values were taken from Ref. [30] .
![]()
Figure 10. The comparison of proton emission spectra of 197Au (n, p) reaction at 14 MeV neutron energy. Experimental values were taken from Ref. [26] .
spectrum in shape but the data obtained from EXFOR give higher results than theoretical estimation especially in low and high energy regions. The neutron emission spectra produced by 197Au(p, n)197Hg reaction calculated using HM is compared with the experimental data in Figure 11. The obtained theoretical spectrum is in a relatively good agreement with the experimental data. Moreover, the HM result gives lowest result in low energy region.
4. Conclusion
Several conclusions can be drawn from the present study. The results for binding
![]()
Figure 11. The comparison of neutron emission spectra of 197Au (p, n) reaction at 22 MeV neutron energy. Experimental values were taken from Ref. [26] .
energies and rms radii of the selected target nuclei calculated using the SHF method with SkM parameterization are more close to the experimental data than that of the calculated results with the other Skyrme parameterizations. Good general agreement has also been found in extensive comparisons of measured nuclear charge-density distributions with calculated using the SkM Skyrme parameterization. The SHF method is the useful for calculating of the spherical nuclei because this force is central and has zero range interactions. For proton and neutron induced PE reactions, the initial neutron and proton exciton numbers can be calculated from the corresponding neutron and proton densities using an effective Skyrme force. HM gives a smooth continuous PE spectra, whereas the experimental results are quite different for each target nuclei, showing the effects of nuclear structure on the PE spectra.HM failed to reproduce the emission spectra in low energy region for medium target nuclei whereas it is succeeded in light and heavy nuclei.