Animal and Plant Species in Antagonistic and Mutualistic Networks, a Multispecies Mean Field Model ()
1. Introduction
Since the seminal paper [1] , the stability complexity debate has evolved to a hot topic in theoretical ecology [2] [3] . From a mathematical perspective, the sta- bility complexity problem can be posed in at least two different contexts: firstly, the traditional approach of population dynamics, a set of coupled differential equations representing the density of a set of many interacting species [1] [4] [5] [6] . In this framework, the main idea is to work the stability of the fixed points of the equations describing the time evolution of the populations [7] . On the other side, the stability complexity problem can be formulated using a more contemporary framework, namely the network theory [8] [9] [10] . In this approach, the focus is on the number, distribution, or assortativity of interac- tions, in one word: the pattern of connections in the network [11] [12] .
In this work, we explore both mathematical approaches. Firstly, the coupled dynamic system is a flexible schema that permits a modeling of complex systems using phenomenological parameters such as the intrinsic growth rate of a popu- lation, its carrying capacity, or the interaction strength among species. All cited parameters can, in principle, be empirically estimated [13] . In addition, most empirical data available to compare with dynamic system models are records of food webs or pollinator networks which indicate the presence of interaction among a set of species. Confident time series records of populations interacting in a community are not available, but network inventories of interaction among species are common in the literature. We cite as examples web interaction inven- tories [14] , pollinators flower networks [15] host parasite networks [16] , and herbivory networks [17] .
In this manuscript, we work with a dynamic multi-species model representing two different situations: mutualistic and antagonistic interactions. Pollination webs are formed by species which both profit from the interaction and then should be favored by adaptive forces. On the other hand, Herbivory (trophic) webs are formed by bipartite webs in which only herbivores profit. This is dif- ferently from pollination where in this case the plants are injured in the inter- action and adaptive forces involved in the interaction are opposite to what found in pollination. We consider a set of  animal species and a set of
animal species and a set of 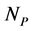 plant species that interact with each other, but do not interact among themselves. The objective of this paper is to construct a Multispecies Mean Field Model MMFM reducing the original
plant species that interact with each other, but do not interact among themselves. The objective of this paper is to construct a Multispecies Mean Field Model MMFM reducing the original 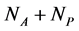 equations to two equations that represent the average animal and plant species. In this approach, the set of coupled dynamic equations may have an intricate topology with many fixed points, limit cycles, strange attractors, or even chaos because of the intrinsic non-linearity [18] . The reduced MMFM, as we shall see, has just one single fixed point of interest. Despite the strong simplification in this methodology, we extract useful hints about network properties, espeacially regarding the network pattern related to the stability of interacting systems, a key point in the complexity stability debate. We are aware that the MMFM that we present here lacks a rigorous mathe- matical foundation. However, we persist in this theoretic field because of the promising results we have found until now.
equations to two equations that represent the average animal and plant species. In this approach, the set of coupled dynamic equations may have an intricate topology with many fixed points, limit cycles, strange attractors, or even chaos because of the intrinsic non-linearity [18] . The reduced MMFM, as we shall see, has just one single fixed point of interest. Despite the strong simplification in this methodology, we extract useful hints about network properties, espeacially regarding the network pattern related to the stability of interacting systems, a key point in the complexity stability debate. We are aware that the MMFM that we present here lacks a rigorous mathe- matical foundation. However, we persist in this theoretic field because of the promising results we have found until now.
In this paper, we consider a MMFM of a dynamic system of coupled Lotka Volterra like equations. The MMFM is a simplified two-dimension version of a multiple dimension system. The Lotka Volterra equations we deal with in our manuscript correspond to linear functional responses in the interaction term [19] [20] , while we discuss more involved non-linear responses in the text. The analysis of the conditions for existence of the MMFM reveals some properties of the complex many dimensional dynamic network underlying the complex dyna- mics.
The main result of the cited paper of May [1] is that ecological networks are sparse. This conclusion is somewhat unexpected, we cite MacArthur that beli- eved that large number of interaction will stabilize networks and not the oppo- site [21] . Our work also uses a coupled of differential equations to model ecolo- gical webs. In contrast, we use different technique and our main findings con- cern differences between antagonistic and mutualistic networks. Our manuscript shows a theoretical model that explains the difference between the number of plant and animals in herbivorous and pollinator networks. The rest of the paper is organized as follows: in Section 2, we present the full multiple dimension dynamic system used to describe the model and the associated MMFM. In Section 3 we separately compare the existing conditions for mutualistic and antagonistic networks with empirical data. Finally, we present our main findings in Section 4 and discuss the number of animal and plants in the community.
2. Methodology
This section is divided in two parts. Initially, we expose the biological data used to test the methodology, namely the set of binary and quantitative interaction networks. The second part of the methodology is devoted to describe the mean field model that is in the center of our analysis.
2.1. The Biological Data Set
In this work, we employed a set of quantitative webs extracted from the lite- rature. We use a total of 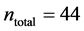 quantitative webs divided into two catego- ries: pollinators
quantitative webs divided into two catego- ries: pollinators 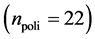 and herbivory
and herbivory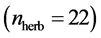 . Pollinator webs are a typical example of a mutualistic networks formed by flowering plants and polli- nator animal species, [22] [23] . Herbivory webs are a well studied example of antagonistic interaction, these networks are formed by herbivorous insect spe- cies and their respective host plants [24] .
. Pollinator webs are a typical example of a mutualistic networks formed by flowering plants and polli- nator animal species, [22] [23] . Herbivory webs are a well studied example of antagonistic interaction, these networks are formed by herbivorous insect spe- cies and their respective host plants [24] .
The empirical objects used in this work are ecological interaction webs which essentially are matrices of size  versus
versus 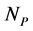 corresponding to two groups of interacting animal and plant species, respectively. In the case of an interaction between species
corresponding to two groups of interacting animal and plant species, respectively. In the case of an interaction between species  of the first set and species
of the first set and species 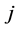 of the second the matrix element is
of the second the matrix element is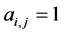 , otherwise
, otherwise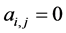 , for the binary case. In the more general case of quantitative matrices
, for the binary case. In the more general case of quantitative matrices 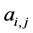 can assume any positive value. The connec- tivity of an animal species is defined as
can assume any positive value. The connec- tivity of an animal species is defined as 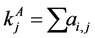 and for a plant species
and for a plant species![]() . The empirical data used in this work is the same of the reference [25] , where we show the full characteristic of the interacting networks. The herbivorous and pollinator webs used in this work are the totality of available webs in the literature at the time of the computation analysis. That means, we have not performed any exclusion criterion in the statistical analysis. The indices of the network we use are: the number of plant
. The empirical data used in this work is the same of the reference [25] , where we show the full characteristic of the interacting networks. The herbivorous and pollinator webs used in this work are the totality of available webs in the literature at the time of the computation analysis. That means, we have not performed any exclusion criterion in the statistical analysis. The indices of the network we use are: the number of plant ![]() and animal species
and animal species![]() , the total number of connections (without weight) among plant and animal
, the total number of connections (without weight) among plant and animal
species![]() , and the connectance
, and the connectance![]() .
.
2.2. The Mean Field Approximation
We employ a model that is a close extension of the multispecies model develo- ped in the reference [26] . We extend the previous work to a model that encom- passes both mutualistic and antagonistic interactions. The theory is based on a two-species model proposed in the reference [2] for the mutualistic case but it is even older in the antagonist situation [27] . The evolution of the animal ![]() and plant
and plant ![]() abundances in time is achieved by:
abundances in time is achieved by:
![]() (1)
(1)
where ![]() and
and ![]() represent the abundances of plant
represent the abundances of plant ![]() and animal
and animal![]() ;
; ![]() and
and ![]() are the growth rates of plants
are the growth rates of plants ![]() and
and ![]() while
while ![]() and
and ![]() are the respective intraspecific competition coefficients. In addition,
are the respective intraspecific competition coefficients. In addition, ![]() and
and ![]() are the per-capita effects of animal
are the per-capita effects of animal ![]() on plant
on plant![]() , and vice-versa. The positive signal of
, and vice-versa. The positive signal of ![]() models a mutualistic dynamic, the effect of animals on plants is positive, so it implies in an increase in plant species abundance. On the other hand, a negative signal models an antagonistic interaction in which animal species restrict plant species growth.
models a mutualistic dynamic, the effect of animals on plants is positive, so it implies in an increase in plant species abundance. On the other hand, a negative signal models an antagonistic interaction in which animal species restrict plant species growth.
We adopt a mean field approach that simplifies the model allowing further analytical insight. The reference [26] used a similar reduction technique to approximate modeling. Indeed, such reductions are common in theoretical eco- logy [27] . We assume that all plant species are equivalent, which means![]() ,
, ![]() ,
,![]() ; and the same average equivalence is applied to animals:
; and the same average equivalence is applied to animals:![]() ,
, ![]() ,
,![]() .
.
![]() (2)
(2)
Moreover, we assume in the mean field approach that![]() . This means, we average the individual elements of the adjacency matrix by the con- nectance of the matrix. In addition, we use the notation
. This means, we average the individual elements of the adjacency matrix by the con- nectance of the matrix. In addition, we use the notation ![]() and
and ![]() . The above equations become:
. The above equations become:
![]() (3)
(3)
We perform the equations’ average for the set of animal and plant species in
the following way. We add all ![]() in the above equation and divide the result
in the above equation and divide the result
by![]() , the number of equations. Next, we introduce
, the number of equations. Next, we introduce![]() ; a simi- lar estimation is performed on the equations of plant species. In addition, we assume that the approximations
; a simi- lar estimation is performed on the equations of plant species. In addition, we assume that the approximations ![]() and
and ![]() are valid in the case differences inside the groups
are valid in the case differences inside the groups ![]() and
and ![]() are not significant. This con- dition is assumed in the mean field approximation. Following these estimations we obtain:
are not significant. This con- dition is assumed in the mean field approximation. Following these estimations we obtain:
![]() (4)
(4)
Finally, we use ![]() and
and ![]() to find:
to find:
![]() (5)
(5)
We are aware that the mean field statement employed in the analytical treat- ment that reduces the dimension of the system from ![]() to
to ![]() is accompanied by a brutal loss of information [28] [29] . However, despite this strong assumption, the model produces theoretical estimations that encourage further development of the concept. We use the notation for the equilibrium solution:
is accompanied by a brutal loss of information [28] [29] . However, despite this strong assumption, the model produces theoretical estimations that encourage further development of the concept. We use the notation for the equilibrium solution: ![]() and
and![]() . With help of this notation we can write the equilibrium points of the MMFM as:
. With help of this notation we can write the equilibrium points of the MMFM as:
![]() (6)
(6)
There are four solutions for this pair of coupled system: the trivial null solu- tion![]() , a solution with absence of plants
, a solution with absence of plants![]() , another with absence of animals
, another with absence of animals ![]() and a non-trivial solution with
and a non-trivial solution with ![]() and
and ![]() positives given by:
positives given by:
![]() (7)
(7)
![]() (8)
(8)
We note that any solution is biologically feasible only for ![]() and
and ![]() posi- tives. Bellow, we develop this point in detail for mutualistic and antagonistic networks. We chose to drop the
posi- tives. Bellow, we develop this point in detail for mutualistic and antagonistic networks. We chose to drop the ![]() symbol in the last equation, instead we adopt
symbol in the last equation, instead we adopt ![]() for mutualistic interactions and
for mutualistic interactions and ![]() for herbivory.
for herbivory.
2.3. Discussion of a Nonlinear Model
We may also consider more sophisticated mutualistic models that take into account a non-linear saturation process as in the reference [19] [20] . We remark that the nonlinear model, as any ordinary differential equation model, is a mean field approach; to expand our methodology to a non mean field regime we would have to explicitly include the space by using differential partial equations or cellular automata models [12] . The linear mutualistic model presents an exp- losive behavior that can be solved using saturation in the interaction response between animal-plant. In reference [20] the mutualistic interaction for one animal and one plant species ![]() and
and ![]() is modeled as:
is modeled as:
![]() (9)
(9)
However, for low handling time![]() , the non-linear equations reduce to the standard linear model. The main point in model choice is perhaps: how far are the linear model predictions compared to the non-linear one. The result of re- ference [20] is interesting, as it shows that the critical points of the non-linear model are in a broader interval which include the linear one, and the two models coincide in the limit of small non-linearity. In addition, the analytical treatment of the non-linear model is mathematically cumbersome and less intuitive than the linear case. Moreover, the linear model allows us to explicitly make analytical inferences and to test them. Despite its simplification, the linear model produces sound theoretical results that can be compared with empirical data.
, the non-linear equations reduce to the standard linear model. The main point in model choice is perhaps: how far are the linear model predictions compared to the non-linear one. The result of re- ference [20] is interesting, as it shows that the critical points of the non-linear model are in a broader interval which include the linear one, and the two models coincide in the limit of small non-linearity. In addition, the analytical treatment of the non-linear model is mathematically cumbersome and less intuitive than the linear case. Moreover, the linear model allows us to explicitly make analytical inferences and to test them. Despite its simplification, the linear model produces sound theoretical results that can be compared with empirical data.
3. Condition for Existence of the Mean Field Model
In our work, we study network properties and analyze what the MMFM can tell about network patterns that produce viable communities. In this way, we do not focus on species parameter![]() ,
, ![]() ,
, ![]() and
and ![]() but on the interaction network properties:
but on the interaction network properties: ![]() and
and ![]() at one side and network parameters:
at one side and network parameters:![]() ,
, ![]() and
and![]() .
.
We distinguish two situations in the study: the mutualistic interactions and the antagonistic interactions. The first is characterized by a positive effect of the plant animal encounter on plant population growth ![]() whereas the second shows the opposite tendency that plant-animal interactions decrease plant growth
whereas the second shows the opposite tendency that plant-animal interactions decrease plant growth![]() . In the following, we distinguish these two situations to study MMFM conditions for the existence of viable solutions.
. In the following, we distinguish these two situations to study MMFM conditions for the existence of viable solutions.
3.1. Mutualism
The condition for non-trivial existence of the system formed by Equations (7) and (8) assumes that both ![]() and
and ![]() should be positive. Since the numera- tor of the right side of equation is always positive, in order to fulfill both con- ditions it is necessary that the denominator will be positive. Then, we have:
should be positive. Since the numera- tor of the right side of equation is always positive, in order to fulfill both con- ditions it is necessary that the denominator will be positive. Then, we have:
![]() (10)
(10)
This inequality imposes that the quantities![]() ,
, ![]() ,
, ![]() ,
, ![]() or
or ![]() should be small. The condition of small product
should be small. The condition of small product ![]() and connectance
and connectance ![]() is related to sparsity and it is a well known property of ecological networks [15] [22] . Moreover, the condition of small product
is related to sparsity and it is a well known property of ecological networks [15] [22] . Moreover, the condition of small product ![]() was explored in reference [28] , where it is interpreted as the effect of asymmetric dependence in mutua- listic networks. The limitations of the linear approach in this context was discu- ssed in reference [20] .
was explored in reference [28] , where it is interpreted as the effect of asymmetric dependence in mutua- listic networks. The limitations of the linear approach in this context was discu- ssed in reference [20] .
3.2. Antagonism
In the case of antagonistic interactions, we perform the transformation
![]() . In this new situation, the denominator of Equations (7) and (8) will always be positive, and as a consequence, Equation (7) is trivially positive. The fixed point related to Equation (8) still has an additional condition that should be fulfilled:
. In this new situation, the denominator of Equations (7) and (8) will always be positive, and as a consequence, Equation (7) is trivially positive. The fixed point related to Equation (8) still has an additional condition that should be fulfilled:
![]() (11)
(11)
This new condition imposed to antagonistic systems implies that ![]() should be small, which means that the overall number of links in an antagonistic web should not be large. The simplest way to guarantee this condition is that the number of animals in the web,
should be small, which means that the overall number of links in an antagonistic web should not be large. The simplest way to guarantee this condition is that the number of animals in the web, ![]() , should be small. We call attention that this condition is not present in mutualistic networks, therefore antagonistic webs should have a comparatively small number of animal species. We compare the number of animal and plant species for mutualistic and antagonistic cases in the next subsection.
, should be small. We call attention that this condition is not present in mutualistic networks, therefore antagonistic webs should have a comparatively small number of animal species. We compare the number of animal and plant species for mutualistic and antagonistic cases in the next subsection.
3.3. Data Comparison
The condition for existence (11) which is exclusive of antagonistic networks claims that ![]() should be small. In this way, we expect that the number of animals in antagonistic networks should be more restricted than the number of plants.
should be small. In this way, we expect that the number of animals in antagonistic networks should be more restricted than the number of plants.
The relative difference between animals and plants is presented in Figure 1. In this picture we show a bar-plot comparing the ratio ![]() for all pollinators and herbivorous webs. In addition, we performed the Student’s t-test to check for difference between the groups
for all pollinators and herbivorous webs. In addition, we performed the Student’s t-test to check for difference between the groups![]() ,
, ![]() ,
,![]() . We per- formed an extra test to check if the number of animals for herbivorous data set is significantly distinct from the number of plants
. We per- formed an extra test to check if the number of animals for herbivorous data set is significantly distinct from the number of plants![]() ,
, ![]() ,
, ![]() , which gives a negative result.
, which gives a negative result.
4. Discussion
In this paper, we work a multidimensional dynamic model that encompasses
![]()
Figure 1. The figure shows the ratio![]() , the number of animal species divided by plant species in the network. The figure shows a larger relative number of animals in pollinator networks as compared to herbivorous networks. We depict a constant dashed line
, the number of animal species divided by plant species in the network. The figure shows a larger relative number of animals in pollinator networks as compared to herbivorous networks. We depict a constant dashed line ![]() to help the visualization.
to help the visualization.
mutualistic and antagonistic interactions in a single framework. The MMFM is based on reducing a set of ![]() coupled equations to two equations that describe the dynamic evolution of a paradigmatic animal and plant of the com- munity. At one hand, the MMFM implicates in a loss of information of the individual species and their interactions. On the other hand, the MMFM allows for computing the existence conditions of the system, and as a consequence, to make inference about these conditions of the full multispecies interaction net- work.
coupled equations to two equations that describe the dynamic evolution of a paradigmatic animal and plant of the com- munity. At one hand, the MMFM implicates in a loss of information of the individual species and their interactions. On the other hand, the MMFM allows for computing the existence conditions of the system, and as a consequence, to make inference about these conditions of the full multispecies interaction net- work.
The essence of Mean Field approach in theoretical science consists in erasing individual differences to capture overall features of the system. In a mean field approximation, the interaction details among individuals in a network are less important than the average properties of the system dynamics. The challenge of the Mean Field Theory consists in not taking into account superfluous heter- ogeneities of the problem, but instead focusing on overall aspects of the pheno- menon. The objective of the Mean Field theory is neither to give answers to in- dividual differences, nor to look at small differences in the system. In this pers- pective, the MMFM still gives answers that can be empirically verified, despite obvious limitations and strong reductionism. The dependence asymmetry and the sparsity of the networks are positive results of the Mean Field approach and have already been discussed in the literature [26] . The difference between animal and plant species has not previously explored, and our work is the first to point out this theoretical result of the MMFM. In summary, the Mean Field Theory should be judged a posteriori. If the theoretical model gives a positive answer to empirical data, only then can it be taken seriously.
The idea that antagonistic interactions are more modular like, whereas mu- tualistic ones are more nested was extensively explored in the literature [15] [30] . The antagonistic relations tend to follow an arms race co-evolutionary strategy that produces a formation of cliques in the network, while the mutua- listic interactions point to a generalist plus sub-generalist co-evolutionary strate- gy [31] . Our manuscript works out another, not so explored, difference between antagonistic and mutualistic networks: the number of animal and plants in their composition. In fact, an alternative and appealing title for our paper could be: “Why pollinator networks have more animals than plants in their structures than herbivorous networks?” This paper essays an explanation for this question, in fact, this is the objective of our work.
It is well known that biodiversity of animal species is larger than plant species [32] [33] [34] . Following this simple rule, we should generally expect that the number of animal species should surpass the number of plant species in intera- cting networks. This expectation could be used as a null model for plant and animal species occupancy in an interacting network. Our theoretical results suggest that it is not valid for antagonistic interaction networks, which is in agreement with empirical results. In this way, as stated in Figure 1, pollinator networks are closer to a null model of animal and plant occupancy than antag- onistic networks which present a strong misbalance in their composition.
Finally, we believe that this work is important for the discussion of the com- plexity stability debate. We are conscious of the strong simplification of our mathematical framework. Initially we propose a model of coupled differential equations that is already a mean field approach because it does not take into account the spatial structure of the landscape. Over this model we proceed to perform a further simplification, reducing the number of variables from ![]() to 2. In this way, our theoretic approach proceeds over a double mean field approximation: first, we exclude the spatiality, and secondly we reduce the number of degrees of freedom. A comparison of our results with empirical data suggest that despite the strong simplification of our theoretical approach, the mean field strategy is indeed a valuable tool.
to 2. In this way, our theoretic approach proceeds over a double mean field approximation: first, we exclude the spatiality, and secondly we reduce the number of degrees of freedom. A comparison of our results with empirical data suggest that despite the strong simplification of our theoretical approach, the mean field strategy is indeed a valuable tool.
Acknowledgements
Financial support to Gilberto Corso from CNPq (Conselho Nacional de Desen- volvimento Científico e Tecnológico) is acknowledged.