Improved Measurement Method of Circularly-Polarized Antennas Based on Linear-Component Amplitudes ()
1. Introduction
Circularly-polarized (CP) antennas have many advantages such as insensitivity to polarization locations, elimination of the signal Faraday rotation effect caused by the ionosphere, and strong anti-interference ability. Therefore, they are wi- dely used in satellite communication, radar, GPS and other systems. It is very important to measure their characteristics of axial ratio (AR), rotation sense, pattern and so on. By means of the measurement based on circular components, it is easy to measure CP antennas [1] . However, the auxiliary CP antennas with high polarization purity are rare in reality, so the uncertainty of this method is relatively large. While linearly-polarized antennas can achieve high polarization isolation easily, so it’s more effective to study the method of measuring the CP antenna based on linear components.
Two methods about measuring ARs of CP antennas based on linear components are discussed in [2] . The first method is to measure one set of orthogonal LP amplitudes and phases by utilizing linearly-polarized auxiliary antennas. Another method is to measure only two sets of orthogonal LP amplitudes without phase measurement. ARs and patterns are separately obtained in [3] [4] [5] by using the first method. However, the phase measurement is limited by measuring equipment and the error is relatively large in fact. The characteristics of ARs are got by utilizing the second method in [6] and [7] . It is not necessary to measure phase information, while amplitudes can be measured accurately. As a result, the measuring accuracy of AR is improved. But this method also has a problem that the rotation sense of the co-polarization cannot be determined due to the absence of the phase information. There is no analysis about this problem in the related records.
An improved measurement method of CP antennas based on linear-compo- nent amplitudes is proposed in this paper. It is the first time to point out the problem that the rotation sense of the co-polarization cannot be determined. And a solution is presented to determine the rotation sense by using common CP auxiliary antennas. In addition, some particular cases with large errors occur in practical measurement, here revises and improvements are given. Finally, co- polarization and cross-polarization patterns are further obtained from AR results. To verify this improved method, a self-developed CP microstrip array was measured repeatedly. The measured results are in agreement with the simulated results, which prove the correction method is correct, effective and practical.
2. Measurement Based on Linear-Component Amplitudes and Phases
The polarization state of the electromagnetic wave is distinguished by the orientation of its electric field vector. In the propagation direction of electromagnetic wave, the electric field vector moves around a circle. According to the orbit of the vector, the electromagnetic waves can be divided into linearly-polarized wa- ves, circularly-polarized waves and elliptically-polarized waves. The transverse electromagnetic wave of antenna radiation in the far field is called plane polari- zed wave, and its arbitrary polarization state is elliptical polarization, as shown in Figure 1. The AR is defined as the ratio of the major axis 2A and the minor axis 2B of the polarization ellipse, denoted as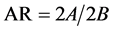 . While A = B, AR = 1 and it is expressed as circular polarization. While A ≠ 0 and B = 0,
. While A = B, AR = 1 and it is expressed as circular polarization. While A ≠ 0 and B = 0, 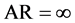 and it is expressed as linear polarization. It can be seen that linear polarization and circular polarization are two particular cases of elliptical polarization [8] .
and it is expressed as linear polarization. It can be seen that linear polarization and circular polarization are two particular cases of elliptical polarization [8] .
The elliptically-polarized wave can be decomposed into two orthogonal linearly- polarized waves [9] . As shown in Figure 1, for arbitrary electric field vector E, it can be decomposed into two orthogonal components Ex along x-axis and Ey along y-axis. For the plane with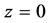 , Ex and Ey can be expressed as:
, Ex and Ey can be expressed as:
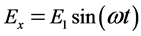 (1)
(1)
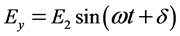 (2)
(2)
where in E1 and E2 are the horizontally-polarized amplitude and the vertically- polarized wave amplitude respectively. 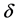 is the phase difference between E1 and E2.
is the phase difference between E1 and E2.
In Figure 1, u-axis and v-axis coincide with major axis and minor axis of polarization ellipse. So the semi-major axis A and semi-minor B can be expressed as [10] :
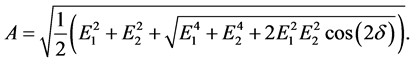 (3)
(3)
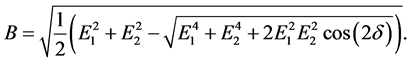 (4)
(4)
τ is the inclination of the polarization ellipse with respect to 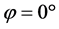 and its expression is:
and its expression is:
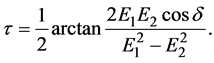 (5)
(5)
Comprehensive above, by measuring one set of orthogonal amplitudes E1, E2 and phase difference 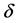 with a linearly-polarized antenna, the AR can be obtained as follows:
with a linearly-polarized antenna, the AR can be obtained as follows:
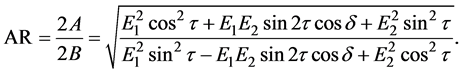 (6)
(6)
The rotation sense of the elliptically-polarized wave can be determined by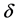 . It is left-handed circular polarization when
. It is left-handed circular polarization when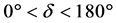 , while it is right-han- ded circular polarization when
, while it is right-han- ded circular polarization when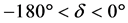 .
.
In general antenna test environment, usually it is difficult to obtain accurate phase information. However, accurate measurement on amplitude is much easier to implement, so it has unique significance to study the measurement on AR only based on linear-component amplitudes.
3. Measurement Only Based on Linear-Component Amplitudes
3.1. Derivation of Phase Information
AR cannot be obtained by Equations (5) and (6) when only using two linear- component amplitudes without phase information. Here a derivation of phase is given from four linear-component amplitudes.
In the xy plane, as shown in Figure 1, the projection of electric field vector E in arbitrary polarization direction of  can be expressed as:
can be expressed as:
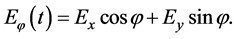 (7)
(7)
Equations (1) and (2) are substituted into the above equation and the following equation can be derived:
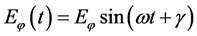 (8)
(8)
where in
![]() (9)
(9)
Equation (9) gives the relationship between ![]() and
and![]() , and its corresponding graph is called polarization graph, as shown in Figure 1. The graph gives the maximum projection of E in the direction of
, and its corresponding graph is called polarization graph, as shown in Figure 1. The graph gives the maximum projection of E in the direction of![]() . Actually,
. Actually, ![]() is the field response of the linearly-polarized antenna rotating to the direction of
is the field response of the linearly-polarized antenna rotating to the direction of ![]() in the xy plane. The maximum and minimum values of the polarization graph coincide with the maximum and minimum values of the polarization ellipse, respectively.
in the xy plane. The maximum and minimum values of the polarization graph coincide with the maximum and minimum values of the polarization ellipse, respectively.
Given two sets of arbitrary orthogonal linear-component amplitudes, phase information can be obtained when they are substituted into Equation (9). For example, through rotating linearly-polarized antenna, two sets of orthogonal LP amplitudes E1, E2, E3, E4 at φ = 0˚, 90˚, 45˚, 135˚ can be obtained, phase can be derived by Equation (9), as follows:
![]() (10)
(10)
3.2. Derivation of AR
By substituting Equation (10) into Equations (5) and (6), ![]() and AR can be obtained:
and AR can be obtained:
![]() (11)
(11)
![]() (12)
(12)
Equation (12) is the formula about measuring AR by utilizing only four amplitudes. Also because of the principle that total power of arbitrary two orthogo- nal components is the same:
![]() (13)
(13)
it can be seen that E4 is redundant. So sometimes, only three amplitudes E1, E2, E3 have to be measured. However, the measurement accuracy can be controlled by utilizing four amplitudes. Therefore, it is better to use the method by utilizing four amplitudes.
3.3. Determination of the Rotation Sense of Co-Polarization
Phase information represented by Equation (10) can be obtained from above derivation. However, the range of arcos ![]() is
is![]() , so the range of
, so the range of ![]() cannot be determined whether it is (0˚, 180˚) or (−180˚, 0˚). This means that the method loses part of phase information, so the rotation sense of co-polarization cannot be determined. This problem has not been mentioned in the related records.
cannot be determined whether it is (0˚, 180˚) or (−180˚, 0˚). This means that the method loses part of phase information, so the rotation sense of co-polarization cannot be determined. This problem has not been mentioned in the related records.
Here a determination method is given by adopting two CP auxiliary antennas with identical structure but reversed rotation senses. Two auxiliary antennas are separately used to measure the amplitude of the antenna to be measured. Then the rotation sense of the co-polarization is the rotation sense of the auxiliary antenna which can measure larger amplitude. It is unnecessary to adopt the CP auxiliary antenna with high polarization purity used in the measurement based on circular components. Here CP auxiliary antennas with general performance are used and they are easy to be implemented in the actual situation.
3.4. Treatment of Particular Cases in Measurement
When the electric field wave approaches linear polarization in particular directions, there will be particular cases with large errors in the measurement. Four kinds of LP cases in particular directions are shown in Figure 2. And their values of normalized amplitudes, ![]() and τ are recorded in Table 1.
and τ are recorded in Table 1.
For the two cases in Figure 2(a) and Figure 2(b), the numerator and denomi- nator of Equation (10) are all close to 0. It causes relatively large errors since ![]() may be greater than 1. Although
may be greater than 1. Although ![]() can be stably solved from Equation (11), errors are still large. However, for the two cases in Figure 2(c) and Figure 2(d), |cosδ| can be solved accurately. Thus for the two cases in Figure 2(a) and Figure 2(b),
can be stably solved from Equation (11), errors are still large. However, for the two cases in Figure 2(c) and Figure 2(d), |cosδ| can be solved accurately. Thus for the two cases in Figure 2(a) and Figure 2(b), ![]() can be accurately obtained from Figure 2(c) and Figure 2(d). Let
can be accurately obtained from Figure 2(c) and Figure 2(d). Let ![]()
![]()
![]()
![]() then
then
![]() (14)
(14)
![]() (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 2. LP cases in particular directions.
![]()
Table 1. Normalized amplitudes, ![]() and
and ![]() values of LP cases.
values of LP cases.
![]() (15)
(15)
![]() (16)
(16)
In practice, the particular case of ![]() appears occasionally. In this case, performance of circular polarization is pretty good. However, the numerator and denominator of Equation (11) are all close to 0,
appears occasionally. In this case, performance of circular polarization is pretty good. However, the numerator and denominator of Equation (11) are all close to 0, ![]() has a large error as a result. While δ approximately equals to ±90˚ by utilizing Equation (10), then AR can be accurately obtained through dividing Equation (3) by Equation (4).
has a large error as a result. While δ approximately equals to ±90˚ by utilizing Equation (10), then AR can be accurately obtained through dividing Equation (3) by Equation (4).
3.5. Derivation of Patterns
Co-polarization and cross-polarization can be obtained from AR results as follows. The elliptically-polarized wave can also be decomposed into two orthogonal CP waves with reversed rotation senses. For arbitrary electric field vector E, it can be decomposed into right-handed CP component ![]() and left-handed CP component
and left-handed CP component![]() . If
. If![]() , the right-hand CP component is co-polarization component and the left-hand CP component is cross-polarization component, otherwise the opposite.
, the right-hand CP component is co-polarization component and the left-hand CP component is cross-polarization component, otherwise the opposite. ![]() and
and ![]() satisfy the following relations:
satisfy the following relations:
![]() (17)
(17)
AR can also be expressed by![]() ,
, ![]() (suppose that
(suppose that![]() ):
):
![]() (18)
(18)
Let![]() , then
, then
![]() (19)
(19)
Substitute ![]() into Equation (17), then
into Equation (17), then
![]() (20)
(20)
![]() (21)
(21)
Therefore, patterns of the antenna to be measured can be represented by (20) and (21), corresponding to the co-polarization component and the cross-polari- zation component, respectively.
4. Measurement Verification
A self-developed CP microstrip array shown in Figure 3 was measured repeatedly by using the improved method. The CP antenna to be measured in Figure 3 is used as a receiving antenna and rotates with the turntable. And the linearly- polarized double-ridged horn shown in Figure 4 is kept still as a transmitting antenna.
![]()
Figure 4. Linearly-polarized double-ridged horn.
The polarization direction of the linearly-polarized transmitting antenna is se- parately rotated at 0˚, 90˚, 45˚ and 135˚, and four linearly-polarized amplitudes can be measured quickly and accurately. Then ARs and patterns can be solved from above derivations based on the amplitudes conveniently. The measured re- sults are compared with the simulation results, as shown in Figures 5-7. The si- mulation results are derived from Ansoft HFSS.
![]()
Figure 5. Curves of ARs versus frequency (![]() ).
).
![]()
Figure 6. Curves of ARs versus ![]() at center frequency of 8.6 GHz (
at center frequency of 8.6 GHz (![]() ).
).
![]()
Figure 7. Normalized patterns at center frequency of 8.6 GHz (![]() ).
).
Measured results in Figure 5 show that the AR curves versus frequency agree very well with the simulated one from 8.47 GHz to 8.68 GHz. The minima are both about 1.5 dB at the center frequency of 8.6 GHz. There are only some certain differences at lower or upper frequencies, which can be attributed to the machining tolerance. At the center frequency of 8.6 GHz, measured and simulated curves of ARs versus ![]() at
at ![]() also maintain good consistency in Figure 6. By utilizing common auxiliary antennas with determined rotation sen- ses, the antenna to be measured is identified as a left-hand CP antenna. The measured and simulated normalized patterns shown in Figure 7 also match well. In patterns, when the LP case occurs, the co-polarization component is approximately equal to the cross-polarization component, which causes that two components cannot be distinguished. This is the limitation of the proposed work. However, in this case the amplitudes of two components both are small and slight effect occurs on the overall performance of the patterns. It can be solved with nearest distribution according to the smoothness of the curves. Two components of other parts in patterns are clear and can be distinguished easily.
also maintain good consistency in Figure 6. By utilizing common auxiliary antennas with determined rotation sen- ses, the antenna to be measured is identified as a left-hand CP antenna. The measured and simulated normalized patterns shown in Figure 7 also match well. In patterns, when the LP case occurs, the co-polarization component is approximately equal to the cross-polarization component, which causes that two components cannot be distinguished. This is the limitation of the proposed work. However, in this case the amplitudes of two components both are small and slight effect occurs on the overall performance of the patterns. It can be solved with nearest distribution according to the smoothness of the curves. Two components of other parts in patterns are clear and can be distinguished easily.
To sum up, it can be seen that the improved method is correct, practical and effective.
5. Conclusion
A method for measuring characteristic parameters of CP antennas is discussed based on linear-component amplitudes in this paper. By measuring two arbitra- ry sets of orthogonal LP amplitudes, the ARs can be obtained quickly and conve- niently. However, the rotation sense of co-polarization cannot be determined in original measurement method, so here a corresponding solution is presented to determine it by using common CP auxiliary antennas. Also the particular cases in the measurement are considered and perfect processing method has been established. The revised and improved method has the advantages of accuracy, convenience and efficiency. It can meet the basic demand of scientific research and engineering for CP antenna measurement.
Grant Information
This work was supported by National Natural Science Foundation of China under Grant 61401208.