1. Introduction
The time is considered in Mechanics as one of the four coordinates (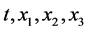 ) in the “space of events,” where
) in the “space of events,” where 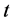 is the “moment of time” when the event takes place and
is the “moment of time” when the event takes place and 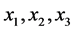 are coordinates of the “place of event” [1] [2] . Hard sticks are standards for measuring of coordinates of “places of events” and periodical movements (clocks) are standards for measuring of “moments of time”. Definition of standards means that the space of events can be investigated by physical methods, and it was established that three coordinates
are coordinates of the “place of event” [1] [2] . Hard sticks are standards for measuring of coordinates of “places of events” and periodical movements (clocks) are standards for measuring of “moments of time”. Definition of standards means that the space of events can be investigated by physical methods, and it was established that three coordinates 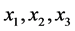 describe three- dimensional Euclidean space. This space looks, intuitively, as understandable one because its standards have dimensionality of length. On the other hand, time does not look understandable on the basis of notions from everyday life. Here we show in the framework of the low-dimensional model that time can be also considered as coordinate with dimensionality of length in some special many- dimensional space. It means that notions “space” and “time” can be reduced to the one notion―coordinates of some space with definite geometry.
describe three- dimensional Euclidean space. This space looks, intuitively, as understandable one because its standards have dimensionality of length. On the other hand, time does not look understandable on the basis of notions from everyday life. Here we show in the framework of the low-dimensional model that time can be also considered as coordinate with dimensionality of length in some special many- dimensional space. It means that notions “space” and “time” can be reduced to the one notion―coordinates of some space with definite geometry.
The formal geometrical interpretation of time is known where time is considered as an imaginary fourth coordinate with the dimensionality of length in the four dimensional pseudo Euclidean space (Minkowski space) [1] . But representation of time by means of imaginary numbers does not give the opportunity to understand reasons of deep difference between notions “space” and “time”. Instead of Minkowski space, the geometrical model of the space of events is considered where all coordinates are real numbers. The space in this model is a topological product of the usual Euclidean space and some another space.
This work is a соntinuation of author’s investigations of possibility to explain physical phenomena by geometrical properties of the space-time [3] [4] [5] [6] . In these investigations the idea was used about increasing dimensionality of our Euclidean space from three to four―the idea firstly used by Kaluza and then by Bergmann and Einstein in their attempts to geometrize electromagnetic field [7] [8] . The idea about additional dimensionalities is the main idea of this work, and this idea is based on the hypothesis that the space of events is a special case of the topological product of the usual Euclidean space and some space with the topology of closed manifold.
2. Low-Dimensional Model of the Space-Time
One of the simplest examples of topological products of spaces is shown at Figure 1. This is a surface of the usual cylinder that can be considered as topological product of one dimensional Euclidean space and one dimensional circle.
Topological products of spaces are a particular case of fiber spaces, and the theory of fiber spaces are now in the course of development [2] . The object of this presentation is to show principal possibility of geometrical interpretation of time, and for this purpose we suggest here the simplest low-dimensional model of the space of events. Namely, we consider the space that is shown at Figure 1. Here the lower straight line is the one dimensional analogy of our three dimensional Euclidean space, and the surface of cylinder (with the above mentioned straight line) is the analogy of the suggested model of the space-time.
Let us consider motions of free bodies in empty space that is motions without external fields of force. As in general relativity, we suggest that motions of such bodies take place along geodesic lines of the empty space-time, that is along shortest pathes between points of this space. Shortest pathes on the cylinder’s surface are segments of the screw lines on this surface. Recall known relations for a screw line [9] (Figure 2).
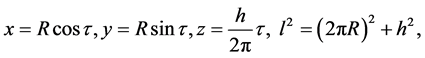 (1)
(1)
![]()
Figure 1. Examples of product of spaces.
where 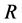 is the cylinder’s radius,
is the cylinder’s radius,  is a length of the pitch of screw,
is a length of the pitch of screw, 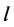 is a length of the one turn.
is a length of the one turn.
Consider the motion of a free body along the screw line with a small pitch of screw, when
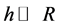 . (2)
. (2)
Then the displacement 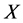 of this body in the Euclidean one dimensional space will be after
of this body in the Euclidean one dimensional space will be after  turns
turns
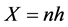 . (3)
. (3)
And the corresponding path 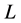 along the screw line will be
along the screw line will be
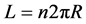 . (4)
. (4)
It follows from (3) and (4) that
 . (5)
. (5)
Replace here  by the variable
by the variable ![]() with the dimensionality of time using relation
with the dimensionality of time using relation
![]() , (6)
, (6)
where ![]() is the light velocity in vacuum. Then (5) can be rewritten as
is the light velocity in vacuum. Then (5) can be rewritten as
![]() (7)
(7)
where
![]() . (8)
. (8)
We show now that above variable ![]() can be interpreted as a time-coordinate in the space of events. The coordinate
can be interpreted as a time-coordinate in the space of events. The coordinate ![]() in (5, 7) denotes the displacement of contact with one dimensional Euclidean space of the free body moving along the screw line in additional dimension (Figure 3).
in (5, 7) denotes the displacement of contact with one dimensional Euclidean space of the free body moving along the screw line in additional dimension (Figure 3).
This displacement looks as a sequence of periodical appearances and disappearances of this body in Euclidean space. But for sufficiently small ![]() these discontinuous displacements will look for observers in Euclidean space as continuous movement because of high frequency of this process. Indeed, according to (8), the frequency
these discontinuous displacements will look for observers in Euclidean space as continuous movement because of high frequency of this process. Indeed, according to (8), the frequency ![]() of this process for displacements with velocity
of this process for displacements with velocity ![]() corresponding to the pitch of screw
corresponding to the pitch of screw![]() , equals
, equals
![]() . (9)
. (9)
Let us suggest that ![]() has a microscopic dimension
has a microscopic dimension![]() . Then
. Then
![]()
Figure 3. Discontinuous displacements in Euclidean space.
![]() . (10)
. (10)
Discontinuous displacements with such high frequencies will be detected as continuous ones by any of modern devices.
And here is the main point. If displacements of free bodies, described by (7), can be considered as continuous ones then (7) should be considered as the law of motion of free bodies in the Euclidean space, that is as the Galilei’s inertia law. And this will be the case only if we identify variable ![]() in (7) as “time”. The variable
in (7) as “time”. The variable ![]() is defined by (6) through the length of free bodiy’s trajectories along geodesic lines. In result, the geometrical interpretation of notion “time” looks as follows: time of a free body’s displacement at distance
is defined by (6) through the length of free bodiy’s trajectories along geodesic lines. In result, the geometrical interpretation of notion “time” looks as follows: time of a free body’s displacement at distance ![]() in Euclidean space equals to the length
in Euclidean space equals to the length ![]() of the trajectory of the same body in additional dimension divided by the light velocity
of the trajectory of the same body in additional dimension divided by the light velocity ![]() Notice that according to (2, 8) this interpretation is valid for motions with nonrelativistic velocities
Notice that according to (2, 8) this interpretation is valid for motions with nonrelativistic velocities ![]()
3. Conclusions
It is shown that within the framework of the suggested model of the space-time there is no fundamental difference between notions “space” and “time”: both of them are represented by coordinates of the one space with specific geometry. It was shown also that there is a one-to-one correspondence between time coordinate (length of the body’s displacement along the screw geodesic line) and the same body’s displacement in the Euclidean space. This means that any kind of motion in Euclidean space can be chosen as a standard for measuring of time. Periodical movements (clocks) happened to be the most convenient in operation.
Notice in conclusion that suggested low-dimensional model of the space-time has mainly a methodical value. This work indicates at possible geometrical structure of the real space of events, namely, a topological product of our three-dimensional Euclidean space and the space with a topology of some closed manifold.