Contribution to the Modeling of a Solar Adsorption Refrigerator under the Climatic Conditions of Burkina Faso ()
1. Introduction
Cold production is mainly achieved by compression machines whose operation requires the use of refrigerants and excessive consumption of electrical energy. These refrigerants, CFCs (chlorofluorocarbons), HCFCs (hydrochlorofluoro- carbons) and HFCs (hydrofluorocarbons) are harmful to the ozone layer and contribute to an increase in the greenhouse effect. Since the Montreal Protocol in 1987, international agreements have been signed to reduce emissions of these refrigerants [1] . Thus, research efforts focused on the development of refrige- ration technologies, which respond to environmental and energy concerns, have been undertaken. Solar adsorption refrigeration machines have been the subject of numerous studies [2] [3] [4] .
These machines are an alternative to solve both ecological and energy problems. Indeed, the technology of these machines is simple, maintenance is easy, and the materials used, are recyclable [5] . In addition, these machines use refrigerants such as water [6] , methanol [7] and ammonia [8] , which have no effect on the environment. For countries such as Burkina Faso, with favorable sunshine with an average irradiation between 5.5 kWh・m−2・day−1 and 65 kWh・hm−2・day−1 [9] , solar adsorption refrigeration is a promising solution to meet important needs such as food preservation, pharmaceuticals, air conditioning, etc. and also to reduce electricity consumption.
However, some disadvantages have become obstacles to the actual application and marketing of these machines such as discontinuous cycle operation [10] [11] , low coefficient of performance, poor heat and mass transfer in the bed Adsorbent [12] , low thermal conductivity of the adsorbent [13] [14] [15] , poor contact between the surface of the adsorber and the adsorbent [16] [17] .
To improve the performance of solar adsorption refrigeration machines, numerous research axes have been proposed, studied and tested. Thus, several solar collector models have been used by researchers to optimize the solar radiation received through use: vacuum tube collectors [18] [19] [20] of the single-glazed or double-glazed (TIM) flat plate collectors [21] [22] [23] , cylindro-parabolic collectors [24] [25] .
Other approaches based on the shape of the adsorber have been used to improve the efficiency of solar radiation. Thus, flat, tubular adsorbers, equipped with external or internal fins, have been used in several prototypes of adsorption solar refrigerators. These fins act as thermal bridges between the absorbent plate and the reactive (porous) medium and thus optimize the heat and mass transfer in the adsorbent bed [12] [17] [26] [27] [28] .
In addition, some researchers have focused on improving the thermal conductivity of adsorbents through the development of composite adsorbent. The technique for preparing the consolidated composite adsorbents consists in adding a material having a higher thermal conductivity to the powder of the conventional solid adsorbent. By this technique, thermal conductivity of the order of 5 to 15 W/m・k can sometimes be reached and a heat exchange coefficient with the metal walls of the adsorber ranging from 200 to 3000 W/m2・k [26] [29] [30] [31] [32] [33] .
In addition, to overcome the intermittent character of the solar adsorption refrigeration cycle, prototype models of machines have been developed. These machines consist of two beds of adsorbents operating so that one adsorbs the refrigerant and the other one desorbs it. Thus, they make it possible to produce cold continuously [7] [34] [35] [36] .
The efficiency of the operation of the refrigerating machines is also linked to the climatic conditions of the site in which the machine is located. Thus, several experimental studies on prototypes of adsorption solar refrigerators have been proposed and tested, in order to find their actual behavior [23] [37] [38] [39] [40] .
The main objective of this study is to contribute to the understanding of the solar refrigeration system by adsorption through a dynamic modeling of a solar adsorption refrigerator model operating under the climatic conditions of Bur- kina Faso.
2. Materials and Methods
2.1. Description of the Cycle of Operation of the Solar Adsorption Refrigerator
A solar refrigerating adsorption machine operates in a cycle. It consists in a flat plate collector containing the zeolite/water mixture and plays a role of capturing and releasing the heat. It is connected to a condenser and an evaporator. The principle of operation of these machines is based on the phenomena of adsor- ption-desorption of a gas (water vapor) in a solid (zeolite). This chemical reac- tion is exo or endothermic according to its direction of unwinding. This ideal cycle represents the evolution of the state of the adsorbent/adsorbate mixture contained in the collector-adsorber. Each cycle includes two main stages gover- ning the operation: one stage for heating the zeolite/water mixture and another for cooling the same mixture.
2.1.1. Heating Phase
・ Isosteric heating phase (1 → 2)
At the beginning of the cycle (point 1), the zeolite/water mixture is at its minimum temperature  (adsorption temperature) and at the pressure
(adsorption temperature) and at the pressure  (evaporation pressure); at this time, the collector-adsorber is isolated. Under heating, the pressure and temperature of the mixture increase, while the total mass of adsorbed water remains constant along the transformation (1 → 2) and equal to
(evaporation pressure); at this time, the collector-adsorber is isolated. Under heating, the pressure and temperature of the mixture increase, while the total mass of adsorbed water remains constant along the transformation (1 → 2) and equal to . This pressurization phase ends as soon as the pressure becomes equal to that prevailing in the condenser
. This pressurization phase ends as soon as the pressure becomes equal to that prevailing in the condenser 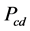 (point 2). The temperature reached is called desorption threshold temperature
(point 2). The temperature reached is called desorption threshold temperature .
.
・ Condensation desorption phase (2 → 3)
This phase begins when the pressure of the mixture in the adsorber reaches the condensation pressure  (saturation pressure corresponding to the temperature of the condenser), the adsorber is placed in communication with the condenser and the desorption of the refrigerant begins, which condenses in the condenser thereafter. The adsorber is then in high pressure and follows the isobar imposed by the condenser. While continuing heating, the temperature of the mixture in the adsorber increases to the maximum temperature
(saturation pressure corresponding to the temperature of the condenser), the adsorber is placed in communication with the condenser and the desorption of the refrigerant begins, which condenses in the condenser thereafter. The adsorber is then in high pressure and follows the isobar imposed by the condenser. While continuing heating, the temperature of the mixture in the adsorber increases to the maximum temperature  (regeneration temperature) at point 3, set for the corresponding cycle. This phase is generally called generation because it is that which makes the adsorber conducive to a new phase of refrigeration production.
(regeneration temperature) at point 3, set for the corresponding cycle. This phase is generally called generation because it is that which makes the adsorber conducive to a new phase of refrigeration production.
2.1.2. Cooling Phase
・ Isosteric cooling phase (3 → 4)
In contrast to the first phase, cooling of the zeolite/water mixture begins at point 3, where the temperature and pressure decrease until the pressure becomes equal to that in the evaporator. The temperature reached is referred to as the adsorption threshold temperature  (point 4). The total mass of the adsorbed fluid remains constant during this phase and is equal to
(point 4). The total mass of the adsorbed fluid remains constant during this phase and is equal to .
.
・ Adsorption-evaporation phase (4 → 1),
This phase is the motor phase of the cycle during which the cold is produced. At point 4, the evaporation of the refrigerant begins, producing cold in the evaporator. The vapor produced is adsorbed again in the adsorber until the temperature of the zeolite water mixture becomes minimal , set for the corresponding cycle. During the transformation (4 → 1), the system follows the isobara imposed by the evaporator and which corresponds to the saturation pressure of the refrigerant (water) at the evaporation temperature. At this point, the machine is ready for a new cycle.
, set for the corresponding cycle. During the transformation (4 → 1), the system follows the isobara imposed by the evaporator and which corresponds to the saturation pressure of the refrigerant (water) at the evaporation temperature. At this point, the machine is ready for a new cycle.
Figure 1 shows the basic thermodynamic route of such a machine in the Clapeyron diagram (LnP; -1/T) (Figure 2).
![]()
Figure 1. Theoretical cycle of an adsorption machine.
![]()
Figure 2. Photography of solar adsorption refrigerator.
2.2. Modelisation
The mathematical model presented below simulates the real operation of the solar adsorption refrigeration system taking into account the variation in solar radiation and the ambient temperature during the day. Thus, we present the modeling of the transfer of heat and mass in the adsorbent bed, and the balance equations at each compartment of the system (glass, absorbent plate, condenser, and evaporator).
2.2.1. Assumptions
The formulation of some assumptions is necessary for an approximate simulation of the system. Thus we assume that:
・ The porous material (adsorbent) is assimilated to a medium having a temperature T and equivalent thermal conductivity,
・ Heat transfer is unidirectional,
・ The convective heat transfer and the pressure losses are neglected in the porous medium,
・ The pressure remains constant in the condenser and in the evaporator.
2.2.2. Equations Balances
The heat transfer equations at each part of the refrigerator can be written as follows:
The glass
 (1)
(1)
The absorbent plat
 (2)
(2)
The adsorbent bed
During the isosteric heating and desorption phase
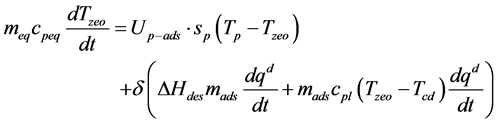 (3)
(3)
During the isosteric cooling phase and adsorption
 (4)
(4)
With:
 : During isosteric heating and cooling;
: During isosteric heating and cooling;
 : During desorption and adsorption;
: During desorption and adsorption;
The condenser
![]() (5)
(5)
The evaporator
![]() (6)
(6)
2.2.3. Model of Adsorption Kinetics
Several theories of adsorption have been proposed in the literature to describe the process of the adsorption and desorption phenomenon. The Dubinin-As- takhov equation is used successfully to describe the adsorption of gas vapor on the adsorbent. Thus, this equation is used to calculate the rate of adsorbate (water) in the zeolite (adsorbent) as a function of temperature and pressure.
![]() (7)
(7)
where ![]() is the density of the adsorbate (water) and
is the density of the adsorbate (water) and ![]() is the saturation pressure.
is the saturation pressure. ![]() is the maximum adsorption capacity; D and n are constants pedending on the adsorbent/adsorbate couple used.
is the maximum adsorption capacity; D and n are constants pedending on the adsorbent/adsorbate couple used.
2.2.4. System Performance
The solar performance coefficient (SCOP) of a solar refrigerating machine is defined as the ratio between the amount of cold produced at the evaporator and the total solar energy incident for a full day.
![]() (8)
(8)
where As is the collecting surface and Gn is the solar flux in W/m2 ![]() is the amount of cold produced at the evaporator, given by:
is the amount of cold produced at the evaporator, given by:
![]() (9)
(9)
2.3. Numerical Methodology
2.3.1. Initial and Boundary Conditions
For all![]() ,
, ![]() being the instant from which the collector-adsorber is subjected to the solar flux, we have:
being the instant from which the collector-adsorber is subjected to the solar flux, we have:
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
2.3.2. Method of Resolution
The method of solving the system of equations which describes the transient behavior of the model is purely numerical and based on the implicit finite difference method and the Gauss Seidel iterative method. We have developed and written in Fortran a computer program to model and simulate the adsorption- desorption kinetics of the zeolite/water pair and on the other hand the operation of each element of the refrigerator during a day.
3. Results and Discussion
3.1. Validation of the Model
In order to validate our numerical code, we applied our code to the solar adsorption refrigerator model presented by A. Allouhi et al. [41] . This model describes a parallelepiped-shaped collector-adsorber refrigerator using the silicagel-water couple. A comparison between the changes in the temperature in the adsorbent bed as a function of its pressure, describing the Clapeyron cycle of the solar adsorption refrigerator, shows good quantitative agreement. Indeed, the maximum deviation observed for the temperatures is of the order of 1.1% and 2.4% for the pressure (Figure 3).
3.2. Climatic Data
Solar radiation and ambient temperature are parameters that affect the performance of solar refrigeration systems. Thus, using the weather data provided by the General Direction of Meteorology in Burkina Faso (DGM), which include the values of the monthly global radiation densities on a horizontal plane in J/cm2, we used the method of Liu and Jordan to transform these data in order to obtain the hourly values of the global radiation on an inclined plane of angle 12.2˚ with respect to the horizontal. For ambient temperature, we used the data of E. Ouédraogo et al. [42] , who carried out a statistical study to develop an hourly weather file for the city of Ouagadougou. Thus, Figure 4(a) and Figure 4(b)
![]()
Figure 3. Comparison of the Clapeyron cycle given by A. Allouhi and our calculation code.
![]()
Table 1. Main parameters used in the simulation.
![]() (a)
(a)![]() (b)
(b)
Figure 4. Hourly evolution of solar radiation and ambient temperature.
shows the hourly evolution of global solar radiation and the ambient temperature for December, August, October and March. It can be seen that the radiation is maximum in March and minimal in August, this can be explained by the clear sky in March and by a sky low in October and December. In August, this is due to the presence of dust and clouds. These values thus obtained and the values in Table 1 were used for the simulation of our model.
3.3. Dynamic Behavior of the Solar Refrigerator
Figure 5 shows the evolution of the temperature of the glass, the absorbent plate and the adsorbent bed (zeolithe) as a function of time during the four phases of
![]()
Figure 5. Time evolution of the temperature of the various components of the solar refrigerator for the month of March.
the cycle. At the beginning of the cycle (the initial state), the temperatures are uniform and equal to the adsorption temperature, which in turn equals the ambient temperature at sunrise. When the solar flux increases, the collector-ad- sorber heats up and the temperatures of its various components increase rapidly with time. They each reach a maximum (Tv = 358 K, Tp = 396 K, Tzeo = 395 K) at about 13 o’clock. The maximum temperature of the adsorbent bed is referred to as the regeneration temperature, that is to say the temperature at which there is no heat exchange between the plate and the adsorbent bed. When the solar flux decreases, the collector-adsorber cooling begins. The temperatures of the various compartments decrease until the temperature reaches 300 K. This temperature represents the temperature in which there is no exchange between the glass pane, the plate and the adsorbent bed.
The evolution of the temperature of the condenser during the cycle is also shown in Figure 5. At the beginning of the cycle, the temperature of the condenser is the same as that of the ambient. This is explained by the fact that the condenser is isolated from the collector-adsorber during this period. When the desorption-condensation phase begins, the self-contained valve opens and the desorbed water vapor flows into the condenser, resulting in an increase in its temperature. At about 14 o’clock, the temperature of the condenser reaches its maximum at Tcd = 320 K, after which it begins to decrease. This increase in condenser temperature is due in large part to the latent heat of condensation of the water. The decrease of the temperature after 14 o’clock is due, on the one hand, to the cessation of the desorption process and, on the other hand, to cooling by means of the convection and the radiation which the condenser exchanges with the ambient medium. The temperature of the condenser begins to follow that of the ambient temperature during the rest of the day.
The evolution of the temperature of the evaporator is also shown in the same Figure 5. The temperature of the evaporator decreases from 297 K to 275 K. This cooling of the evaporator is due to the evaporation of the condensate (water) from the evaporator to the adsorbent bed. Thus, the adsorbate withdraws the needed heat for phase change of the refrigerating enclosure where the evaporator is located. This results in cooling.
Figure 6 shows the variation of the pressure within the adsorbent bed as a function of time. During the phases of the operating cycle, the pressure has a logical behavior with the evolution of the temperature. It increases rapidly from the evaporation pressure Pev = 872 Pa (equal to the saturation pressure at the evaporation temperature) up to a maximum value corresponding to the condensation pressure Pcd = 7376 Pa (equal to the saturation pressure at the condensation temperature). During the desorption phase, the pressure remains constant and equal to the condensation pressure until the temperature of the adsorbent bed reaches the maximum regeneration temperature. Then, it begins to decrease to the low initial evaporation pressure.
The distribution of the quantity of water adsorbed during the four phases of the cycle is also shown in the same figure. During the cycle, the total quantity of water adsorbed in the adsorbent bed decreases during the desorption phase and then increases during adsorption. It remains constant during the isosteric heating and cooling phases.
3.4. Comparison of the Results of the 4 Months
The evolution of the temperature, the pressure and the quantity of water adsorbed in the adsorbent bed are respectively represented in Figures 7-9. It is clear that the climatic data have a great influence on the Performance of the solar refrigerator. Indeed, for the month of March, the values of the temperature,
![]()
Figure 6. Evolution of the pressure and the adsorbed mass for the month of March.
![]()
Figure 7. Comparison of the evolution of the adsorbed mass during the 4 months.
![]()
Figure 8. Comparison of the evolution of the pressure during the 4 months.
![]()
Figure 9. Comparison of the evolution of the temperature of the zeolite during the 4 months.
![]()
Table 2. Coefficient of performance of the solar adsorption refrigerator.
of the quantity of desorbed adsorbate, are higher compared to the other three months. This is due to the fact that the solar flux density is maximum during this month (990 W/m2). The performances of the solar adsorption refrigerator for the four months are also shown in the Table 2. For the month of March, the SCOP reached is 0.25, while for the other months the SCOP is equal to 0.21 for the month of December, 0.15 for the month of October and 0.11 for the month of August.
4. Conclusions
This work presents the modeling of a system of solar refrigeration by adsorption which uses the couple zeolite and water. Thus, through a mathematical model, we wrote the equations of balance at each part of the refrigerator and developed a program written in Fortran language in order to simulate the behavior of the refrigerator taking into account the climatic conditions of the city of Ouagadougou. The temperature changes of the glass, the absorbent plate, the conden- ser, the evaporator, the adsorbent bed and its pressure and the adsorbed mass were discussed.
The key findings are:
・ For March and December, the average solar flux densities are 590 W/m2 and 514 W/m2 respectively. The amount of cold produced during these months is 6.391 MJ for the month of March and 4.642 MJ for the month of December. This gives a SCOP of 0.25 and 0.21 for the months of March and December.
・ With an average daily solar flux density of 436 W/m2 and 480 W/m2 respectively for the months of August and October, the SCOP reached by our solar refrigeration system is 0.11 and 0.15, with a total product amount of 2.12 and 3.1 MJ.
The dynamic model thus developed allows to predict the real operation of the solar adsorption refrigerator and to evaluate its performance according to the climatic conditions of the city of Ouagadougou (Burkina Faso) for the hottest months and the coldest months of the year. The results obtained are very encouraging to continue to improve the performance of the solar adsorption refrigerator in order to use it in industrial and domestic domains.
Acknowledgements
The authors are grateful to the University Agency of the Francophonie (AUF) and the French Embassy (SCAC) for financial support which allowed the realization of this work.
Nomenclature
Cp
Spécific heat (J/kg.K)
ΔH
Heat of
adsorption/desorption (J/kg)
D
Constant in the Dubinin-Astakhov Equation
Subscripts
Gn
Solar radiation (W/m2)
a
adsorption
m
mass (kg)
ads
adsorbent
n
Constant in the Dubinin-Astakhov Equation
d
desorption
P
Pressure (Pa)
cd
condenser
Ps
Saturation Pressure (Pa)
ev
evaporater
Qf
Cold production (J)
v
glass
q
Water concentration inside the zéolithe (kg/kg)
ext
outside
S
Area (m2)
amb
ambient
T
Température (K)
zeo
zeolithe
t
Time (s)
min/max
minimum
Wo
Parameter of Dubinin-Astrakhov Equation (m3/kg)
max
maximum
L(T)
Latent heat of vaporization (J/kg)
g
generation
Greek Letters:
cv
convection
α
absorptance
moy
average
τ
Transmitance
eau
water
Δt
Time step (s)
![]()
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact epe@scirp.org