The Measurement and Prediction of Flash Point for Binary Mixtures {C1 ~ C3 Alcohols + p-Xylene} at 101.3 kPa ()
1. Introduction
Flammable substances, such as organic solvents, are commonly used in laboratories and industrial processes. The flash point (FP) is one of the most important parameters used to characterize the ignition and explosion hazards of these liquids [1] . The lower flammable limit (LFL) provides information on the fundamental physical and chemical processes of combustion. The FP of a given liquid can be experimentally determined, and the resulting temperature may then be adjusted to the standard sea level atmospheric pressure of 101.3 kPa, the pressure at which a substance emits sufficient vapor to form a combustible mixture with air [2] .
As the temperature increases, there is a concomitant increase in both the vapor pressure and the amount of evaporated, flammable liquid in equilibrium with the air. When the temperature is reached at FP, a simple ignition source is able to combust the vapor mixture [3] . Experimental FP data for the multi- component mixtures have become important in ensuring safe storage of flammable materials and, for this reason, studies for predicting the FP of pure substances and mixtures are increasingly important.
Benzene, toluene and xylene are the most used solvents in the rubber products such as tire manufacturing, rubber bands, rubber gloves and appliance moldings. The several alcohols and their mixtures are very useful in the rubber industry [4] [5] . The most common of these solvents is xylene which is used as a solvent in the manufacturing of chemicals, tires, agricultural sprays, adhesives and coatings, as an ingredient in aviation fuel and gasoline, and as a feedstock in manufacturing various polymers, including phthalic anhydride, isophthalic acid, terephthalic acid and dimethyl terephthalate [6] . The purpose of this study is to determine the FPs for flammable binary mixtures commonly used as industrial solvents such as alcohols and xylene.
In the present work, the FPs at 101.3 kPa were determined using a SETA closed cup flash point tester on the following solvent mixtures: {methanol (1) + p-xylene (2)}, {ethanol (1) + p-xylene (2)} and {2-propanol (1) + p-xylene (2)}. The measured FP data for these binary systems were compared with predicted values from a variety of local composition activity coefficient models, including the Wilson, Non-Random Two-Liquid (NRTL) and UNIversalQUAsiChemical (UNIQUAC)models [7] [8] [9] .
2. Material and Methods
2.1. Materials
Commercial, analytical-grade chemicals were used in this investigation. p-Xylene (C8H10, M = 106.17 g·mol−1, CAS-RN 106-42-3, 99.9 %) was obtained from Fluka Co. Methanol (CH4O, M = 32.04 gmol−1, CAS-RN 67-56-1, 99.9%), Ethanol (C2H6O, M = 46.07 gmol−1, CAS-RN 64-17-5, 99.9%) and 2-propanol (C3H8O, M = 60.10 g·mol−1, CAS-RN 67-63-0, 99.9%) were supplied by J. T. Baker Chemical Co. All of the chemicals were dried using molecular sieves with a pore diameter of 0.4 nm. The water contents of the chemicals were determined by Karl-Fischer titration (using a Metrohm 684 KF-Coulometer) and were found to be less than 6 ´ 10−5 g/g. The purities of the chemicals were assessed by gas chromatography. The reported values for the purities, FPs and UNIQUAC parameters [10] [11] are listed in Table 1.
2.2. Procedure
A SETA closed cup flash point tester (Series 8 SETAFLASH, model 82000-0, Surrey, UK) was used to measure the FPs for the miscible mixture samples. The SETA closed cup flash point tester was operated according to the standard test method, ASTM D 3278 [12] . Detailed descriptions for the measuring system and
![]()
Table 1. The purities and UNIQUAC parameters of chemicals used in this work.
aRef [10] ; bRef [11] .
procedure can be found in the previous work [13] [14] . Mixture samples for the experiments were weighed using a microbalance (Ohaus DV215CD) with a precision of 1 ´ 10−5 g. Further details are also appeared in elsewhere [13] [14] .
3. Results and Discussion
Le Chatelier’s rule [15] for a mixture of flammable vapor and air may be expressed as follows:
 (1)
(1)
where yi is the vapor phase composition of a flammable substance i and LFLi is the lower flammable limit of the pure component i. The LFLi is expressed in relation to the pure component i vapor pressure at its FP,  , as
, as
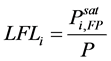 (2)
(2)
where P represents the ambient pressure. The FP of a pure substance is typically measured at standard atmospheric pressure. Under this condition, the vapor phase can be assumed with behaving ideally. With the non-ideal liquid phase containing flammable substances in the presence of the non-condensable components of air, the vapor?liquid equilibrium of component i is described by the modified Raoult’s law:
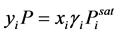 (3)
(3)
where γi is activity coefficient for the liquid phase.
As proposed by Liaw et al. [16] , one can substitute Equation (2) and Equation (3) into Equation (1), resulting in Equation (4), which allows evaluation of FPs for flammable liquid mixtures:
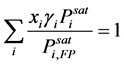 (4)
(4)
The saturated vapor pressure for a pure substance i can be obtained by the Antoine Equation [17] :
 (5)
(5)
Antoine constants (A, B and C in Equation (5)) were adapted from the literature [11] and are given in Table 2.
![]()
Table 2. The Antoine constants of the pure components.
aRef [11] .
Assuming the solution behave ideally, the activity coefficients of the liquid phase are equal to unity. Therefore, Equation (4) was reduced according to Raoult’s law and expressed as [14] :
 (6)
(6)
The temperature that satisfies Equation (6) is obtained to be the flash point of the ideal solution.
For non-ideal liquid mixtures, activity coefficients (γi) were estimated with the optimum binary interaction parameters of the Wilson, NRTL and UNIQUAC equations, described below [6] [7] [8] .
Wilson Equation:
 (7)
(7)
with

NRTL Equation:
 (8)
(8)
with

UNIQUAC Equation:
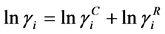 (9)
(9)

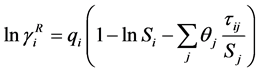
with


The experimental binary FP data for the three systems tested as part of this work, {methanol + p-xylene}, {ethanol + p-xylene} and {2-propanol + p-xylene}, are given in Table 4. The experimentally determined binary data were compared with the predicted values from the Wilson, NRTL and UNIQUAC models. The binary parameters of each model equation were used to calculate the activity coefficients of liquid mixture under the same conditions employed in the experiments, and the initial temperature for calculation was assigned the numerical average FP of the pure components. Then, the FP was obtained from adjustment of initial temperature by satisfying the Le Chatelier’s rule (Equation 4). The objective function (OF) used was
![]() (10)
(10)
The average absolute deviations (A.A.D) between the measured and calculated values are included in Table 4.
A.A.D is defined as:
![]() (11)
(11)
where ![]() is the experimentally determined FP of component i, and
is the experimentally determined FP of component i, and ![]() is the predicted FP of component i.
is the predicted FP of component i.
The data of each binary system at 101.3 kPa pressure are plotted in Figures 1- 3. The parameters for the activity coefficient models are given in Table 3, along with the A.A.D between the experimental and predicted values. All FP data agreed very well, as illustrated in the figures. Minimum flash point behavior was
![]()
Table 3. The optimized binary parameters of the Wilson, NRTL and UNIQUAC equa- tions for each binary system.
aRef [18] ; bRef [19] .
![]()
Table 4. The experimental and predicted FPs for each binary system at 101.3 kPa.
![]()
Figure 1. The comparison of the flash point prediction curves with the experimental data for the binary system {methanol (1) + p-xylene (2)} at 101.3 kPa.
![]()
Figure 2. The comparison of the flash point prediction curves with the experimental data for the binary system {ethanol (1) + p-xylene (2)} at 101.3 kPa.
![]()
Figure 3. The comparison of the flash point prediction curves with the experimental data for the binary system {2-propanol (1) + p-xylene (2)} at 101.3 kPa.
observed in all the binaries. Minimum flash point is caused from minimum boiling azeotrope in vapor-liquid equilibrium of the mixture. Moreover, the minimum flash point behavior values of each binary system were estimated using the best fitted model, NRTL. They are x1 = 0.745, T = 280.03 K for the system {methanol + p-xylene}, x1 = 0.693, T = 283.54 K for the system {ethanol + p-xylene} and x1 = 0.683, T = 284.14 K for the system {2-propanol + p-xylene}.
For the investigated systems, the A.A.D between the predicted and measured FP values were less than 0.85 K, except when calculated by Raoult’s law. Among the models, the NRTL model yielded results closest to the experimentally determined values. The minimum values of A.A.D by NRTL are 0.59, 0.29 and 0.52 K for {methanol + p-xylene}, {ethanol + p-xylene} and {2-propanol + p-xylene}, respectively.
4. Conclusion
Flash point data for {methanol + p-xylene}, {ethanol + p-xylene} and {2-pro- panol + p-xylene} binary systems were determined at atmospheric pressure. Minimum flash point behavior was observed in all three binaries. Moreover, the minimum flash point behavior values of each binary system were estimated using the best fitted model. The measured FP data agreed well with the predicted values derived from the Wilson, NRTL and UNIQUAC models, with the NRTL model providing the most comparable results. The average absolute deviations between the measured and predicted FPs were less than 0.85K.