1. Introduction
Shape is one of the key characteristics for image understanding and computer vision applications. However, using shape information to recognize the objects has proven to be a challenging task for computer vision system as e.g. in image retrieval or object recognition. Finding good shape descriptors and good methods for comparing these descriptors are the crucial issues in such applications. During the past decades, a variety of shape descriptors and matching methods have been proposed in the literature. References [1] [2] [3] [4] review various approaches and methods for shape analysis.
According to [4] , the existing object description and representation approaches are usually sorted into two categories: Region based approaches and contour based approaches. The region based techniques extract features from the whole shape region, while the contour-based methods extract features only from the object’s boundary. The representative approaches in the literature of region based include Invariant Moments [5] , Zernike Moments [6] , Generic Fourier Descriptor [7] and Radon Transform [8] [9] . These region-based approaches are computationally intense and most of them need to normalize the image to achieve common geometrical invariance. The representative approaches in the literature for contour based include Contour Flexibility [10] , Curvature Scale Space [11] , Fourier Descriptors [12] , Shape Contexts (SC) [13] , Inner-Dis- tance Shape Contexts [14] , Distance Sets [15] , Aligning Curves [16] , Height Functions [17] , Shape Signature [18] and integral invariants [19] . These contour descriptors are based on the boundary of a shape; they do not capture the internal structure of the shape, and so they are unsuitable for disjoint shapes or shapes with holes because internal boundary and topological information is used by these descriptors.
In recent years, more attention has been paid to contour based descriptors, which may be due to the fact that humans are considered to recognize shapes by their contours. Inspired by the shape contexts descriptor [13] , typical of the sampled points based approaches, Ref. [20] uses a finite set of points taken from the object’s boundary to represent the shape. The descriptor is called contour points distribution histogram (CPHD). Then CPDH is combined with the Earth Mover’s Distance (EMD) to match and retrieval shapes. The main deficiency of [20] lies in the high matching cost in distance measurement. In order to partly deal with the rotation invariance, EMD is combined with circular shift and mirror matching in [20] and this tactic lead to high time cost. So as to make up for the deficiency of CPDH, this paper suggests employing the minimal circumscribedellipse instead of circle for the histogram construction. We named the new histogram as Elliptic Contour Points Distribution Histogram (ECPDH), which is prior to CPDH in terms of human visual perception because most of the objects of nature are tend to have elongated shapes. ECPDH can obtains more details of the distribution of contour points and describes the object more precisely than that of [20] . Scale and translation invariance are still intrinsic to the ECPDH. For measuring the similarity between ECPDHs, Dynamic Programing (DP) is employed to find the best correspondence that minimizes the Euclidean distance between the histograms of two shapes. The advantage of using DP rather than EMD for measuring the distance between ECPHDs is no need to adopt circular shift matching. As a result, time cost is decreased obviously.
The remainder of the paper is arranged as follows. Section 2 presents the proposed ECPDH descriptor in detail and the DP algorithm is employed to measure the distance between ECPDHs. The experimental results are presented in Section 3. Finally, Section 4 concludes the paper.
2. Method
2.1. ECPDH Descriptor
The most important part of designing a shape matcher is the choice of the shape representation, which has significant effect on the matching step. As can be seen from the real world, most of the shape of the object is usually tend to slim or oval. Based on this, authors suggest to construct the contour points distribution histogram with multiple concentric elliptical grid, as being illustrated in Figure 1. This tactic is quite different from that of [20] . The extracted histogram, namely ECPDH, has stronger ability of shape identification than that of CPDH because of the main direction of the object is embedded in ECPDH. The following sections describe the process of building ECPDH.
The first step of our method is to represent the shapes by the sequences of points sampled from the object contour. In this paper the equidistant sampling is used for the task of shape retrieval. Thus, any input shape is represented by the sequence of points set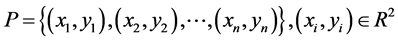 , where
, where 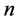 denotes the amount of the sampled points from object contour. The resulted contour points are illustrated in the Figure 1: (a) is the original image; (b) shows the sampled points found using the equidistant sampling technique and its minimum circumscribed ellipse, which is used to building the ECPDH. In this paper, the minimum circumscribed ellipse is determined by Khachiyan’s algorithm [21] [22] . In Figure 1, the pink line is the long axis of the minimum circumscribed ellipse which represents the main direction of the shape. The red star is the ellipse center. The small pink circles are the long axis and ellipse intersection points.
denotes the amount of the sampled points from object contour. The resulted contour points are illustrated in the Figure 1: (a) is the original image; (b) shows the sampled points found using the equidistant sampling technique and its minimum circumscribed ellipse, which is used to building the ECPDH. In this paper, the minimum circumscribed ellipse is determined by Khachiyan’s algorithm [21] [22] . In Figure 1, the pink line is the long axis of the minimum circumscribed ellipse which represents the main direction of the shape. The red star is the ellipse center. The small pink circles are the long axis and ellipse intersection points.
With the extracted and sampled the points from the object contour, the ECPDH descriptor is being constructed. For partly making the ECPDH invariant to rotation, these contour points should be aligned to the main direction. After the main direction of the shape is obtained, then it will be converted in line with the horizontal. These sampled contour points are also rotated to a new location and Figure 1(c) illustrate the aligned results.
Then authors consider the distribution over relative location as a compact and strong descriptor, which is also with high discrimination capability. The region inside the minimum circumscribed ellipse is divided into a few bins with concentric ellipses and uniform interval angles. An illustration of such division is shown in Figure 2. The sampled shape contour points in each bin will be counted and form a histogram which is called ECPDH. ECPDH is very easy to be calculated and has the properties of invariance to translation and scale in nature. Due to the alignment of the shape’s main direction, ECPDH also has rotation invariance. Figure 3 illustrates two instances of the
![]()
Figure 1. The shape and its contour. (a) original shape; (b) sample result; (c) after aligned.
![]()
Figure 2. Distribution of contour points with polar coordinate.
![]()
Figure 3. The instance of shapes and their ECPDHs.
ECPDHs. In Figure 3, (a1) and (b1) show two original phone shape images separately, (a2) and (b2) are the uniformly extracted contour points from (a1) and (b1) respectively, and (a3) and (b3) are the according ECPDHs, respectively. The different color levels of the bins in (a3) and (b3) represent the different numbers of the points located in those bins.
2.2. Distance between ECPDH via DP Algorithm
Many researchers have applied dynamic programming (DP) to the 2D shape matching problem [23] [24] [25] [26] [27] . In the following, we make our definition of shape distance via the DP algorithm using Euclidean distance between the bins in ECPDHs. As [23] [24] [25] [26] [27] , a DP table is also utilized to find the least cost matching between bins of two ECPDHs and the update path is hold along with the diagonal in the DP table. We restrict the path to lie in the area close to the ideal straight diagonal line in order to speed up the matching process (see Figure 4).
In detail, every column in the ECPDH is considered as a vector 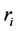 corresponding to the feature of point’s distribution in a sector region in Figure 2. As illustrated in Figure 4, two ECPHDs are put along with the DP table in horizontal and vertical directions, respectively. A vector
corresponding to the feature of point’s distribution in a sector region in Figure 2. As illustrated in Figure 4, two ECPHDs are put along with the DP table in horizontal and vertical directions, respectively. A vector 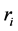 of one of the ECPDH is corresponding to one row or one column in the table.
of one of the ECPDH is corresponding to one row or one column in the table.
Initially, the elements of DP table are set as
![]()
Figure 4. The DP table used for matching ECPDHs.
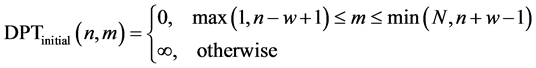 (1)
(1)
where, 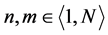 ,
, 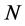 is the number of vectors in ECPDHs,
is the number of vectors in ECPDHs,  is the predefined diagonal width illustrated in Figure 4. Only the elements of DPT that fall within
is the predefined diagonal width illustrated in Figure 4. Only the elements of DPT that fall within 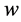 are updated during the DP search.
are updated during the DP search.
Starting at a selected vector for both shape contours A and B, the  is searched, through the diagonal window of width
is searched, through the diagonal window of width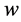 , left-to-right and bottom-to-up starting from the bottom-left element, as shown in Figure 4. The first row and first column elements are initialized as the distances between the corresponding vectors using Equation (2)
, left-to-right and bottom-to-up starting from the bottom-left element, as shown in Figure 4. The first row and first column elements are initialized as the distances between the corresponding vectors using Equation (2)
 (2)
(2)
where, 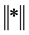 denotes the Euclidean distance between two vectors from the two different ECPDHs.
denotes the Euclidean distance between two vectors from the two different ECPDHs.
Then, the rest of the zero-valued elements of DPT are updated as
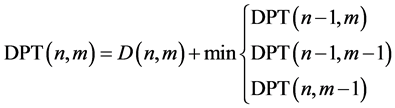 (3)
(3)
The least cost path through the ![]() is the value of element
is the value of element![]() , which corresponds to the best matching between the two ECPDHs. Moreover, in order to obtain the invariance to the horizontal and vertical mirror transformation, one ECPDH is fixed and the other one is reconstructed according to the horizontal and vertical mirror transformation of the original shape. The final least cost correspondence is taken as the minimum value of
, which corresponds to the best matching between the two ECPDHs. Moreover, in order to obtain the invariance to the horizontal and vertical mirror transformation, one ECPDH is fixed and the other one is reconstructed according to the horizontal and vertical mirror transformation of the original shape. The final least cost correspondence is taken as the minimum value of ![]() among three runs of the
among three runs of the ![]() search, denoted by
search, denoted by![]() . Figure 5 illustrates the flow chart for the DP algorithm.
. Figure 5 illustrates the flow chart for the DP algorithm.
![]()
Figure 5. The flow chart for the DP algorithm.
3. Results
This section presents the results obtained using the proposed approach and several sets of experiments are proceeded. The first experiment is proceeded on the sub dataset of MPEG-7 shape dataset (see Figure 6), which is make up of 216 images including 18 categories, and each category includes 12 shapes with variations in form and occlusion of parts. An experimental method referred by [28] suggests that each shape should be used as a query to be matched against all the others, and the results are sorted by the distance between each pair. The nearest matches according to category and the corresponding recognition rates are summarized in Table 1. The results of comparison between the SC [13] and the proposed method is illustrated in Table 2. It is clear that ECPDH combining with DP performs better than that of SC [13] . To give a more comprehensive comparison, the common performance measurement [11] , i.e. precision and recall curves of the retrieval are used here. The precision-recall diagram is illustrated in Figure 7. The results show that ECPDH combining with DP outperforms all the other methods. The parameters used in the experiments are 200 sampled points with ![]() bins and
bins and ![]() is set to 1.
is set to 1.
Furthermore, the whole MPEG-7 shape database (Figure 6) is used to demonstrate scale invariance, rotation invariance and similarity shape query [29] . MPEG-7 shape database is make up of 1400 shapes of 70 categories. Each category has 20 similar shapes. This dataset is used for similarity-based retrieval which tests integral robustness
![]()
Figure 6. Illustration of the MPEG-7 shape dataset.
![]()
Figure 7. Precision-recall curves of different methods on MPEG-7 sub dataset (216 shapes).
of the shape representations. The parameters used in the experiments are 200 sampled points with ![]() bins and
bins and ![]() is set to 1.
is set to 1.
For each retrieval, the precision of the retrieval at each level of the recall is recorded. The final precision of retrieval with a shape descriptor is the average precision of all the retrievals with that shape descriptor. The average precision and recall of the retrieval on each data set are illustrated in Figure 8. We compare the results of the proposed approach with several other common contour based shape analysis methods on Mpeg-7 dataset. As we can see from Figure 8 that the performance of ECPDH + DP is very competitive.
Figure 9 compares the results of precision and recall of the proposed method with different parameters. The selection of different parameters has certain influence on the experimental results. From Figure 9(a) and Figure 9(b), it is clear that when parameter ![]() is fixed and with different parameters
is fixed and with different parameters![]() , the resulted PVR curers are almost overlapping. That is to say the selection of parameter
, the resulted PVR curers are almost overlapping. That is to say the selection of parameter ![]() has little impact on the retrieval performance. Figure 9(c) and Figure 9(d) are partial enlargements of (a) and (b) respectively. From Figure 9(e), it is clear that when parameter
has little impact on the retrieval performance. Figure 9(c) and Figure 9(d) are partial enlargements of (a) and (b) respectively. From Figure 9(e), it is clear that when parameter ![]() is fixed the better result
is fixed the better result
![]()
Table 1. Resulted nearest matches according to category on the sub dataset of MPEG-7 (216 shapes). The values in the table denote the number of nearest matches, and that 12 matches are the most possible. Last row: recognition rate for each nth nearest matches for all in the database. Last column: recognition rates for each category.
![]()
Table 2. Retrieval results compared with SC on MPEG-7 sub dataset (216 shapes).
is achieved with larger![]() . In general, when the parameter
. In general, when the parameter ![]() is selected as 5 and the parameter
is selected as 5 and the parameter ![]() is selected as 24 the experiments can achieve favorable results.
is selected as 24 the experiments can achieve favorable results.
We test the comparison between the proposed method and [20] on the MEPG-7 shape database. The bull’s-eye score and 1NN recognition rate are used for testing the performance in these tests. All the tests do not adopt the circular shift matching in distance measurement. The proposed approach is conducted in Matlab with a core i5, 3.33 GHz PC. An individual pairwise matching takes 4ms on average while the CPDH + EMD takes 40 ms on average. The main reason is that we don't need to use circular shift matching.
![]()
Figure 8. Comparison of PVR Curves (MPEG-7 shape database).
Table 3 shows the compare of the average bull’s-eye score and the recognition rate between CPDH + EMD [20] and ECPDH + DP. It is clear that ECPDH + DP outperforms CPDH + EMD with the same parameters. When the parameter ![]() is selected as 5 and the parameter
is selected as 5 and the parameter ![]() is selected as 24, ECPDH + DP get the average bull’s-eye test with 72.81% and recognition rate with 95.5.
is selected as 24, ECPDH + DP get the average bull’s-eye test with 72.81% and recognition rate with 95.5.
Table 4 shows the comparison of the average bull’s-eye score and the recognition rate between ECPDH + EMD and ECPDH + DP. It is clear from the Table 4, when the ECPDH is used for describing the shape, DP algorithm can obtain better retrieval performance than the EMD algorithm.
Table 5 shows the comparison of the average bull’s-eye score and the recognition rate between CPDH + DP and ECPDH + DP. As it is shown in the Table 4, the proposed ECPDH outperforms the CPDH for both retrieval and recognition rate performances.
Table 6 shows the comparison of the average bull’s-eye score and the recognition rate between ECPDH + EMD and CPDH + EMD. As it is shown in the Table 5, the proposed ECPDH outperforms the CPDH for both retrieval and recognition rate performances again. From Table 5 and Table 6, it is obviously that our proposed ECPDH is more effective than CPDH.
As related in the aforementioned, the ECPDH essentially has the properties of invariance to translation and scale. For the purpose of testing ECPHD’s ability of invariance
![]()
![]()
![]()
Figure 9. Comparison of PVR Curves for different parameters (MPEG-7 shape database).
to rotation and mirror, 10 shape images from the MPEG-7 dataset are selected as benchmark and rotated to form eight new images with![]() ,
, ![]() ,
, ![]() ,
, ![]() in clockwise and anti-clockwise directions, respectively. And the other two new images are produced by mirroring benchmark image in horizontal direction and vertical direction, respectively. The rotation and mirror shape database has 110 images in all, including with the 10 benchmark images. In this new shape database, three retrieval tests were
in clockwise and anti-clockwise directions, respectively. And the other two new images are produced by mirroring benchmark image in horizontal direction and vertical direction, respectively. The rotation and mirror shape database has 110 images in all, including with the 10 benchmark images. In this new shape database, three retrieval tests were
![]()
Table 3. Comparison of average bull’s-eye score and recognition rate between CPDH + EMD and ECPDH + DP.
![]()
Table 4. Comparison of average bull’s-eye score and recognition rate between ECPDH + EMD and ECPDH + DP.
![]()
Table 5. Comparison of average bull’s-eye score and recognition rate between CPDH + DP and ECPDH + DP.
![]()
Table 6. Comparison of average bull’s-eye score and recognition rate between ECPDH + EMD and CPDH + DP.
carried out by using ECPDH + DP, CPDH + DP and CPDH + EMD. In Tables 7-9, the query shapes are shown in the left column and the first 10 sorted nearest neighbors for each query shape are illustrated in the right rows, respectively.
![]()
Table 7. Rotation and mirror invariant retrieval results using ECPDH + DP.
![]()
Table 8. Rotation and mirror invariant retrieval results using CPDH + DP.
![]()
Table 9. Rotation and mirror invariant retrieval results using CPDH + EMD.
Table 7 shows the retrieval illustrations of ECPDH+DP. The left column of the Table 7 lists the 10 benchmark images which are used as query images. All of the front 10 retrieved images, ranked by the distance (similarity) between them and the query image, belong to the same category as the query image. That is to say ECPDH + DP has robust performance of invariance to rotation and mirror.
Table 8 lists the retrieval results of CPDH + DP. The left Colum of the Table 8 lists the 10 benchmark images which are used as query images as well. Compared with the results in Table 7, there are 8 shapes, with blue background color in the table, which have the different category with the query kinds in all the front 10 retrieved images. From the retrieval results, it is easy to conclude that the ECPDH + DP has the stronger ability of invariant to rotation and mirror than that of CPDH + DP.
Table 9 lists the retrieval results of CPDH + EMD. The left column of the Table 9 lists the 10 benchmark images which are used as query images as well. Compared with the results in Table 7, there are also 8 images, with blue background color in the table, which have the different category with the query kinds in all the front 10 retrieved images. We can easily draw conclusion that the ECPDH + DP is prior to CPDH + DP in term of invariance to rotation and mirror too.
4. Conclusion
We introduce a simple contour points based shape descriptor named ECPDH for shape retrieval, which use concentric minimum inscribing ellipse to describing 2D shape. The idea is intuitive and very simple. The proposed ECPDH not only satisfies the human’s visual perception and easy to be implemented, but also it naturally has the attributes of invariant to scaling, translation and rotation. Compared with CPDH, ECPDH can more precisely describe the distribution of object contour points. Embedding the information of the main direction of object is also one of its merits. The authors also suggest using the DP algorithm to measure the distance between ECPDHs. Compared with the EMD algorithm, the time cost is reduced obviously. Several kinds of experiments on MPEG7 shape dataset indicate that our proposed approach achieves favorable results when used for 2D shape image retrieval. The shortage of ECPDH is that it can only describing 2D objects with a single closed contour. This decreases its potential. Extending ECPDH being applied in 3D model description and matching is a promising research direction.
Acknowledgements
The authors would like to thank the anonymous reviewers for their beneficial and constructive advices. This work is supported by National Natural Science Foundation of China (Grant No. 61471182), Natural Science Foundation of Jiangsu Province of China (Grant No. BK20130473), Postdoctoral Scientific Research Foundation of Jiangsu province (Grant No.1402068C).