Novel Soil Strength Criterion Compared with Conventional Criteria ()
1. Introduction
Four criterion models have been used extensively in rock and soil mechanics, including the Mohr-Coulomb (M-C) [1] , the Drucker-Prager yield (D-P) [2] , the Matsuoka-Na- kai (M-N) [3] , and the Lade-Duncan (L-D) [4] . Among those, the M-C, D-P, and M-N models follow the principle that shear stress follows within the main stress element at material failure, with the assumption that the shear plane is in different types. The M-C model assumes that the major and minor principal stress planes introduced at failure will be perpendicular to the shear plane, which also forms an angle of  to the major principal stress, and the shear stress on it is in a linear relationship with the normal stress. Neither shear nor normal stresses are related to the intermediate principal stress, as shown in Figure 1. Furthermore, true triaxial compression test and plane strain test results usually show a shear failure envelope that is nearly identical to this theoretical shear plane.
to the major principal stress, and the shear stress on it is in a linear relationship with the normal stress. Neither shear nor normal stresses are related to the intermediate principal stress, as shown in Figure 1. Furthermore, true triaxial compression test and plane strain test results usually show a shear failure envelope that is nearly identical to this theoretical shear plane.
The D-P strength criterion model is based on the assumption that the octahedral shear stress at failure depends linearly on an octahedral normal stress through material constants. The octahedral shear plane forms the same angle with each plane on which every 2 of the principal stress axes fall (Figure 2).
Based on the M-C criterion’s geometrical description of the shear failure plane, the M-N failure criterion takes into account the intermediate principal stress, leading to the concept of the spatially mobilized plane [3] (Figure 3). In this criterion, the soil body is discretized into a series of cubes of hexahedral elements. When the 3 edges overlap the axes of the 3-dimensional rectangular coordinates, the corresponding intersections of the spatially mobilized plane and the coordinate axes are ,
,  , and
, and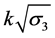 . The angle between the spatially mobilized plane and the major principal stress can be calculated by
. The angle between the spatially mobilized plane and the major principal stress can be calculated by 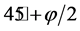 when the axes of the coordinate are either stretched or compressed symmetrically. If the shear planes in the M-C and M-N criterion models are
when the axes of the coordinate are either stretched or compressed symmetrically. If the shear planes in the M-C and M-N criterion models are
![]()
Figure 1. Mohr-Coulomb spatially mobilized plane.
![]()
Figure 2. Octahedral spatially mobilized plane.
![]()
Figure 3. Matsuoka-Nakai spatially mobilized plane.
considered to be spatially mobilized planes as well, the axis intersection points that can be derived from the M-C criterion would be  and
and , and
, and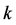 ,
, 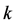 , and
, and 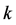 from the D-P criterion, as shown in Figure 1 and Figure 2. They all point out that shear stress on a spatially mobilized plane is proportional to its normal stress at failure, and the strength failure surfaces are all symmetric around the hydrostatic compressive axis in the principal stress space. None of these classic models, including the triaxial compression and tension spatially mobilized plane criterion [5] , which was developed by Sheng-Jun Shao et al., could fully explain the protogenic anisotropy of loess strength. The twin-shear strength criterion [6] proposed by Yu Maohong and L. N. He could calculate the shear stress on both shear planes at material failure, and could also be called a twin spatially mobilized plane criterion.
from the D-P criterion, as shown in Figure 1 and Figure 2. They all point out that shear stress on a spatially mobilized plane is proportional to its normal stress at failure, and the strength failure surfaces are all symmetric around the hydrostatic compressive axis in the principal stress space. None of these classic models, including the triaxial compression and tension spatially mobilized plane criterion [5] , which was developed by Sheng-Jun Shao et al., could fully explain the protogenic anisotropy of loess strength. The twin-shear strength criterion [6] proposed by Yu Maohong and L. N. He could calculate the shear stress on both shear planes at material failure, and could also be called a twin spatially mobilized plane criterion.
In addition to all the models above demonstrating that shear stresses on spatially mobilized planes are in a linear relationship with normal stress, the L-D criterion established the nonlinear relationship between shear stress and mean normal stress described by a power function. However, the L-D criterion does not establish a corresponding spatially mobilized plane. A nonlinear strength criterion was established by Yangping Yao et al. [7] by introducing a power function relationship between shear stress and spherical stress at material failure, and by combining generalized von Mises criterion (corresponding to the circumscribed circle of the M-C strength failure surface) with the M-N strength criterion.
To better describe the strength of loess, this paper introduces a new spatially mobilized plane model that generates the axis intersections as ,
, 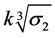 , and
, and , in the same way the spatially mobilized plane does in the M-N criterion. The new model is comparable to the L-D criterion, showing that the L-D criterion is approximative with the strength criterion based on the
, in the same way the spatially mobilized plane does in the M-N criterion. The new model is comparable to the L-D criterion, showing that the L-D criterion is approximative with the strength criterion based on the  spatially mobilized plane, which reveals the physical basis of the L-D strength criterion. The rationality and reliability of the new model were demonstrated by a series of true triaxial tests on intact structural loess. A comparison between the test results and this theoretical prediction is given below.
spatially mobilized plane, which reveals the physical basis of the L-D strength criterion. The rationality and reliability of the new model were demonstrated by a series of true triaxial tests on intact structural loess. A comparison between the test results and this theoretical prediction is given below.
2. The  Spatially Mobilized Plane
Spatially Mobilized Plane
Similar to the M-N proposal of a spatially mobilized plane, the new model is called the ![]() spatially mobilized plane (Figure 4).
spatially mobilized plane (Figure 4).
The spatially mobilized plane could be determined by
![]() (1)
(1)
According to the geometric relationship shown in Figure 4, the directional cosine of this spatially mobilized plane is calculated as, assuming ![]()
![]() (2)
(2)
The cosine of the normal direction of the spatially mobilized plane relating to the axis I is
![]() (3)
(3)
The cosine of the normal direction of the spatially mobilized plane relating to axes II and III are respectively:
![]() (4)
(4)
![]() (5)
(5)
![]()
Figure 4. Stress in the ![]() spatially mobilized plane.
spatially mobilized plane.
Or, the equations could be combined as
![]() (6)
(6)
From which the component of stress on the ![]() spatially mobilized plane along the coordinate axes are derived as
spatially mobilized plane along the coordinate axes are derived as![]() :
:
![]() (7)
(7)
The resultant force on the ![]() spatially mobilized plane is
spatially mobilized plane is
![]() (8)
(8)
Also, the normal stress ![]() and shear stress
and shear stress ![]() would be:
would be:
![]() (9)
(9)
and
![]() (10)
(10)
3. The ![]() Spatially Mobilized Plane Strength Criterion
Spatially Mobilized Plane Strength Criterion
Since shear stress to normal stress on the spatially mobilized plane is a constant value
![]() (11)
(11)
Under triaxial compression![]() , the strength criterion are
, the strength criterion are![]() .
. ![]() is
is
![]() (12)
(12)
![]() in (11) can be replaced with (12):
in (11) can be replaced with (12):
![]() (13)
(13)
With Formula (13), the strength failure envelope in the principal stress space and the strength failure curve on the octahedral plane could be plotted as in Figure 5.
The failure criteria are related only to the internal friction angle for noncohesive soil. After testing soil samples with internal friction angles φ of 5˚, 15˚, 25˚, 35˚, and 45˚, the authors plotted the corresponding strength failure circle on the π plane as shown in Figure 6.
Generalizing the ![]() spatially mobilized plane to cohesive soil, the shear stress and normal stress on the spatially mobilized plane would be
spatially mobilized plane to cohesive soil, the shear stress and normal stress on the spatially mobilized plane would be
![]() (14)
(14)
and
![]() (15)
(15)
and the strength criterion would be
![]()
![]() (a) Strength failure curve surface (b) Strength failure curve on the octahedral plane
(a) Strength failure curve surface (b) Strength failure curve on the octahedral plane
Figure 5. The cube root spatially mobilized plane criterion strength failure envelope.
![]()
Figure 6. The ![]() spatially mobilized plane criterion on the octahedral plane.
spatially mobilized plane criterion on the octahedral plane.
![]() (16)
(16)
while
![]() . (17)
. (17)
4. The L-D Criterion and the ![]() Spatially Mobilized Plane Criterion versus Other Conventional Criteria
Spatially Mobilized Plane Criterion versus Other Conventional Criteria
The D-P criterion can be generated by changing the circumcircle in the M-C criterion. It is also known as a generalized von Mises criterion:
![]() (18)
(18)
The M-N criterion’s criterion is
![]() (19)
(19)
The L-D criterion generated the fitting curve of the failure points, which formed a curved triangle on the octahedral plane, based on the true triaxial test result. The strength curve is in a linear relationship with the average spherical stress on the meridional plane that can be described as
![]() (20)
(20)
or
![]() (21)
(21)
According to the strength failure criterion ![]() under the axisymmetrical compression stress condition, it derives
under the axisymmetrical compression stress condition, it derives
![]() . (22)
. (22)
A comparison of the L-D and the ![]() spatially mobilized plane criteria with the D-P and M-N criteria respectively when the soil internal friction angle was 15˚, 25˚, and 35˚ is plotted in Figure 7. It can be seen that the L-D criterion forms a stress plane
spatially mobilized plane criteria with the D-P and M-N criteria respectively when the soil internal friction angle was 15˚, 25˚, and 35˚ is plotted in Figure 7. It can be seen that the L-D criterion forms a stress plane
very similar to that of the ![]() spatially mobilized plane criterion, and they are all between the D-P and M-N criteria’s strength planes.
spatially mobilized plane criterion, and they are all between the D-P and M-N criteria’s strength planes.
Further, a comparison between the L-D and ![]() spatially mobilized plane criteria versus the M-C, D-P, and M-N criteria is plotted on the octahedral plane with the same meaning principal stresses in Figure 8. It shows the same result: the strength circles of the L-D and
spatially mobilized plane criteria versus the M-C, D-P, and M-N criteria is plotted on the octahedral plane with the same meaning principal stresses in Figure 8. It shows the same result: the strength circles of the L-D and ![]() spatially mobilized plane criteria fall between the D-P criterion strength circle and the M-C and M-N strength circles. In addition, the L-D criterion’s strength curve is identical with that of the
spatially mobilized plane criteria fall between the D-P criterion strength circle and the M-C and M-N strength circles. In addition, the L-D criterion’s strength curve is identical with that of the ![]() spatially mobilized plane criterion.
spatially mobilized plane criterion.
5. The ![]() Spatially Mobilized Plane Criterion and the L-D Criterion
Spatially Mobilized Plane Criterion and the L-D Criterion
The strength failure surface on the principal stress plane and the strength failure circle on the π plane can be derived from the L-D criterion. While the soil internal friction angle increases at 5˚, 10˚, 15˚, 20˚, 25˚, 30˚, 35˚, and 40˚, the strength failure surface and strength failure circle increase their radius at the same time, as shown in Figure 9.
Similarly, for the ![]() spatially mobilized plane criterion, the test result is shown in Figure 10.
spatially mobilized plane criterion, the test result is shown in Figure 10.
The following study reveals how soil shearing resistance changes along with the change of principal stress ratio b under different combinations of soil internal friction angles φ and spherical stresses on the π plane. As shown in Figure 11, the ![]() spatially mobilized plane and the L-D criteria yield identical soil shearing resistances.
spatially mobilized plane and the L-D criteria yield identical soil shearing resistances.
6. The ![]() Spatially Mobilized Plane Criterion and the True Triaxial Test
Spatially Mobilized Plane Criterion and the True Triaxial Test
Loess soil structure strength is highly correlated with the soil’s outstanding physical and structural properties. However, its strength stability drops significantly when it loses its protogenic structure. With the support of data from the Yichuan Xing et al. true triaxial test [8] on loess it can be seen that the strength failure circle on the octahedral plane falls outside of the M-C strength failure line. That test stablished the fitting model on the octahedral plane as well as the proportional relationship between shear stress and average spherical stress.
![]()
![]() (a) Strength failure surface in the principal stress space (b) Strength failure curve on the octahedral plane
(a) Strength failure surface in the principal stress space (b) Strength failure curve on the octahedral plane
Figure 9. The strength failure surfaces of the Lade-Duncan criterion.
![]()
![]() (a) Strength failure surface in the principal strength space (b) Strength failure curve on the octahedral plane
(a) Strength failure surface in the principal strength space (b) Strength failure curve on the octahedral plane
Figure 10. The ![]() spatially mobilized plane criterion failure.
spatially mobilized plane criterion failure.
In this study, the authors conducted true triaxial tests of 4 kinds of intact loesses under conditions of consolidation and drain. Tests were completed with the newly developed true triaxial apparatus, with 70 mm × 70 mm × 140 mm specimens, from the Xi’an University of Technology [9] . The basic physical indices of different loesses are shown in Table 1, in which the liquid limit (LL) and plastic limit (PL) were tested by a conical weight with a 76 g weight penetrating a prepared soil sample to depths of 2 mm and 10 mm. The procedure adhered to the national standard for soil test methods of the People’s Republic of China. The plastic index is the difference between the LL and the PL. The flow index is the ratio of the difference between the moisture content and the PL to the plastic index.
Three confining pressures were applied, 100 kPa, 200 kPa, and 300 kPa, and the intermediate principal stress ratios were controlled at 0.00, 0.25, 0.50, 0.75, and 1.00 (Table 2). The first step of the test procedure was to compress the loess sample with a certain confining pressure until its consolidation. The second step was to separate the drained true triaxial compression with a certain intermediate principal stress ratio until its deconstruction.
Four sets of test results were plotted for each type of loess sample. Figure 12 shows that normal stress is highly linearly correlated with shear stress on the ![]() spatially mobilized plane for every sample set.
spatially mobilized plane for every sample set.
Figure 13 exhibits the theoretical ![]() spatially mobilized plane curve along with the true triaxial test result curve on the π plane for each set. They all have same average spherical stress of 600 kPa, demonstrating consistency between the criterion and the experimental values, and the rationality and reliability of the
spatially mobilized plane curve along with the true triaxial test result curve on the π plane for each set. They all have same average spherical stress of 600 kPa, demonstrating consistency between the criterion and the experimental values, and the rationality and reliability of the ![]() spatially mobilized plane criterion.
spatially mobilized plane criterion.
7. Conclusions
The normal stress plane intersected with each of the major, intermediate, and minor normal stress axes at points![]() ,
, ![]() , and
, and![]() . The surface that all 3 intersection points fell on was defined as the
. The surface that all 3 intersection points fell on was defined as the ![]() spatially mobilized plane.
spatially mobilized plane.
![]()
Table 1. Basic physical indices of loess.
![]()
Table 2. The moisture content and dry density of intact loess.
The ![]() spatially mobilized plane strength criterion projected a strength failure envelope in a conical shape in the stress space and formed a curved triangle shape of strength failure surface on the octahedral plane. It falls on the exterior of the M-C envelope and the M-N cone, but the interior of the D-P cone is identical to the L-D envelope in the stress space.
spatially mobilized plane strength criterion projected a strength failure envelope in a conical shape in the stress space and formed a curved triangle shape of strength failure surface on the octahedral plane. It falls on the exterior of the M-C envelope and the M-N cone, but the interior of the D-P cone is identical to the L-D envelope in the stress space.
On the octahedral plane, the shearing resistances of the L-D criterion and the ![]() spatially mobilized plane strength criterion changed, along with the principal stress ratio b in the same form. This indicated that the L-D criterion and the
spatially mobilized plane strength criterion changed, along with the principal stress ratio b in the same form. This indicated that the L-D criterion and the ![]() spatially mobilized plane strength criterion were essentially identical. The L-D strength criterion was an approximate
spatially mobilized plane strength criterion were essentially identical. The L-D strength criterion was an approximate ![]() spatially mobilized plane strength criterion with a constant shearing stress ratio.
spatially mobilized plane strength criterion with a constant shearing stress ratio.
True triaxial test results verified the linear relationship between shear stress and normal stress on the ![]() spatially mobilized plane. The test results were also comparable with the
spatially mobilized plane. The test results were also comparable with the ![]() spatially mobilized plane strength criterion on the π plane, which demonstrated a rational and reliable relationship of that strength criterion to the strength of loess.
spatially mobilized plane strength criterion on the π plane, which demonstrated a rational and reliable relationship of that strength criterion to the strength of loess.
Acknowledgements
This research was supported by National Natural Science Foundation of China and the Shaanxi Key Laboratory of Loess Mechanics and Engineering of China.