On a Boundary Value Problem for a Polynomial Pencil of the Sturm-Liouville Equation with Spectral Parameter in Boundary Conditions

A. Adiloglu Nabiev

Department of Mathematics, Cumhuriyet University, Sivas, Turkey.

DOI: 10.4236/am.2016.718190                

Abstract

The boundary value problem with a spectral parameter in the boundary conditions for a polynomial pencil of the Sturm-Liouville operator is investigated. Using the properties of the transformation operators for such operators, the asymptotic formulas for eigenvalues of the boundary value problem are obtained.

Keywords

Sturm-Liouville Equation, Boundary Value Problem, Transformation Operator, Spectral Theory of Differential Operators, Asymptotic Formulas, Fractional Derivative, Eigenvalue, Eigenfunction, Polynomial Pencil

1. Introduction

In this paper the boundary value problem, generated on the finite interval 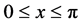by equation

(1)

and the boundary conditions

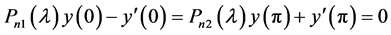(2)

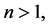
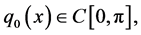
is considered. Here we assume that 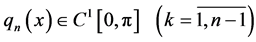are complex valued functions; 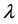is a complex parameter and

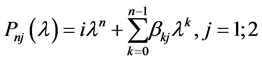
with the given constants.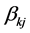

Note that many of these investigations are based on some integral representations for the fundamental solutions of the Sturm-Liouville equation called transformation operators. The transformation operators for Sturm-Liouville equation and quadratic pencil of the Sturm-Liouville equation are constructed and studied in [12] [13] and [14] [15] respectively, while the corresponding operators for the pencil (1) are investigated in [10] [16] .

In this paper using the properties of transformation operators, the considering boundary value problem is investigated and asymptotic formula for the eigenvalues is obtained.

We studied in [10] , the solutions 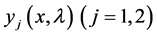of the Equation (1) satisfying the initial conditions

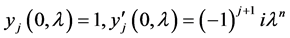
and it is proved that in the sectors of complex plane

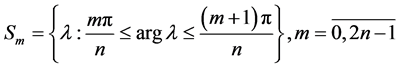
the solutions have the following integral representations:

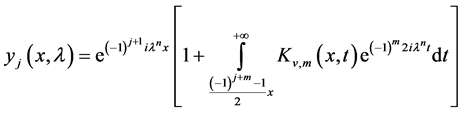(3)

where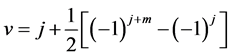, and,

belong to and respectively. Moreover, if denotes Riemann-Liouville fractional derivative of order (see [17] ) with respect to t, i.e.

then for all the functions and belong to and respectively. Furthermore, the following equalities are valid:

(4)

(5)

where

(6)

2. Asymptotic Formulas for the Solutions and Eigenvalues

By and we denote the solutions of the Equation (1) with initial conditions

(7)

Using integral representations (3) and formulae (4), (5), it is easy to show that for each

(8)

(9)

(10)

(11)

Let us consider the boundary problem (1), (2). Denote by the characteristic function of this problem. Then

(12)

Zeros of the function we’ll call eigenvalues of the problem (1), (2). Let be the solution of the Equation (1) with initial conditions

(13)

It is clear that

(14)

and

(15)

From formulae (8)-(11) we find that

(16)

(17)

Then for we can write the asymptotic formula

(18)

where and are constants. From this we conclude that there exists the constant such that

(19)

for all, where

(20)

From (20) we have that for sufficiently large positive integer there are a finite number of zeros of in the circle. In other words, the total number of zeros of in is equal to the total number of zeros of the function Moreover, there exists a positive number such that on the circle the estimation

(21)

satisfies. Hence, from (28), (30) and the equality

(22)

according to Rouche’s theorem we conclude that and have the same number of zeros in the circle for sufficiently large. Using a simple asymptotic estimations (see [2] ), we obtain that zeros having sufficiently large module of the func-

tion lie near rays and so the eigenvalues of the problem (1),

(2) consist of series. Solving the equation asymptotically we find the following asymptotic formula for series of eigenvalues of the problem (1), (2):

(23)

where

Theorem 2. Boundary value problem (1), (2) has a countable number of eigenvalues. The eigenvalues having sufficiently large module are placed near the rays

, and series of these satisfy the asymptotic formula (23).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Fulton, C.T. (1977) Two-Point Boundary Value Problems with Eigenvalue Parameter in the Boundary Conditions. Proceedings of the Royal Society of Edinburgh, 77A, 293-308. https://doi.org/10.1017/S030821050002521X
[2]	Mukhtarov, O.Sh. (1994) Discontinuous Boundary-Value Problem with Spectral Parameter in Boundary Conditions. Turkish Journal of Mathematics, 18, 183-192.
[3]	Altinisik, N., Kadakal, M. and Mukhtarov, O.Sh. (2004) Eigenvalues and Eigenfunctions of Discontinuous Sturm-Liouville Problems with Eigenparameter-Dependent Boundary Conditions. Acta Mathematica Hungarica, 102, 159-193. https://doi.org/10.1023/B:AMHU.0000023214.99631.52
[4]	Wang, A., Sun, J., Hao, X. and Yao, S. (2009) Completeness of Eigenfunctions of Sturm-Liouville Problems with Transmission Conditions. Methods and Applications of Analysis, 16, 299-312. https://doi.org/10.1016/j.jmaa.2008.08.008
[5]	Hinton, D.B. (1979) An Expansion Theorem for an Eigenvalue Problem with Eigenvalue Parameter in the Boundary Conditions. Quarterly Journal of Mathematics: Oxford Journals, 30, 33-42. https://doi.org/10.1093/qmath/30.1.33
[6]	Binding, P., Hyrnyv, R. and Langer, H. (2001) Ellipitic Eigenvalue Problem with Eigenparameter Dependent Boundary Conditions. Journal of Differential Equation, 174, 30-54. https://doi.org/10.1006/jdeq.2000.3945
[7]	Rasulov, M.L. (1967) Methods of Countour Integration. North Holland Publishing Co.
[8]	Shkalikov, A.A. (1982) Boundary Value Problems for Ordinary Differential Equations with a Parameter in Boundary Conditions. Functional Analysis and Its Applications, 16, 324- 236.
[9]	Mamedov, Kh.R. (2010) On an Inverse Scattering Problem for a Discontinuous Sturm-Liouville Equation with a Spectral Parameter in the Boundary Condition. Boundary Value Problems, 2010, Article ID: 171967. https://doi.org/10.1155/2010/171967
[10]	Guseinov, I.M., Nabiev, A.A. and Pashayev, R.T. (2000) Transformation Operators and Asymptotic Formulas for the Eigenvalues of a Polynomial Pencil of Sturm-Liouville Operators. Siberian Journal of Mathematics, 41, 453-464. https://doi.org/10.1007/BF02674102
[11]	Agamaliyev, A. and Nabiyev, A. (2005) On Eigenvalues of Some Boundary Value Problems for a Polynomial Pencil of Sturm-Liouville Equation. Applied Mathematics and Computations, 165, 503-505. https://doi.org/10.1016/j.amc.2004.04.116
[12]	Marchenko, V.A. (1997) Sturm-Liouville’s Operators and Their Application. Kiev.
[13]	Povzner, A.Ya. (1948) On Differential Equations of Type Sturm-Liouville on the Semi Axis. Mathematical Surveys (Mat. Sbornik), 23, 3-52.
[14]	Jaulent, M. and Jean, C. (1972) On an Inverse Scattering Problem with an Energy-Dependent Potential. Annales de l’Institut Henri Poincaré A, 17, 363-378.
[15]	Guseinov, G.Sh. (1985) On Spectral Analisys of Quatratic Pencil of Sturm-Liouville Operators. Doklady Akademii Nauk SSSR, 285, 1292-1296.
[16]	Guseinov, I.M. (1997) On a Transformation Operator. Journal of Mathematical Notes, 62, 206-215. https://doi.org/10.1007/bf02355905
[17]	Samko, S.G., Kilbas, A.A. and Marichev, O.M. (1987) Integral and Derifatives of Fractional Order and Its Applications. Minsk, Nauka and Tekhnika.