1. Introduction
Our universe is hypothesized as belonging to the so called oscillatory class [1] . Such a Universe, since it is involved in a cyclic evolution, cannot properly admit either a beginning or an end. Nonetheless, as later underlined, the beginning of a new cycle can be conventionally fixed. The existence of at least a further spatial dimension is postulated and time is considered as being absolute [2] . We have to suppose that our Universe may oscillate following a simple harmonic motion [3] . Nonetheless, the variations of cosmological distances are to be seen as exclusively metric [4] : In other terms, the amount of space between whatever couple of points remains the same with the passing of time. Figure 1 offers a three-dimensional representation of the hypothesized scenario.
In Figure 1, our Universe is portrayed as a circumference that evolves on the surface of a horn torus, following the so called poloidal direction. Each point of the circumference moves tangentially with a constant speed equal to that of light.
If we denote with R the radius of curvature, with 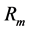 the amplitude of the motion (the mean radius), and with c the speed of light, we can write, with obvious meaning of symbols and signs, the following:
the amplitude of the motion (the mean radius), and with c the speed of light, we can write, with obvious meaning of symbols and signs, the following:
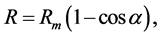 (1)
(1)
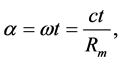 (2)
(2)
 (3)
(3)
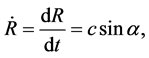 (4)
(4)
 (5)
(5)
The beginning of a new cycle (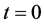 ) is conventionally fixed the precise moment the radius of curvature assumes a null value. The evolution of the hypothesized Universe is evidently characterized by four consecutive phases: an accelerated expansion, a decelerated expansion, a decelerated contraction, an accelerated contraction. All the above-mentioned phases have the same duration.
) is conventionally fixed the precise moment the radius of curvature assumes a null value. The evolution of the hypothesized Universe is evidently characterized by four consecutive phases: an accelerated expansion, a decelerated expansion, a decelerated contraction, an accelerated contraction. All the above-mentioned phases have the same duration.
By taking into account Equations (1) and (4), we can immediately write the so-called Hubble parameter [5] , commonly denoted by H, as follows:
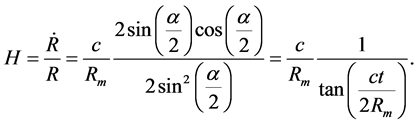 (6)
(6)
As a consequence, it is quite evident how the Hubble parameter may have assumed in the past, and could possibly still assume in the future, negative values.
Let’s consider a material point whose motion is defined by Equation (1) (in other terms, a simple harmonic oscillator consisting of a mass and an ideal spring).
If we denote with m the mass of the above-mentioned point, the elastic constant, denoted by k, can be written as follows:
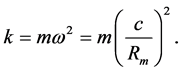 (7)
(7)
Consequently, the total mechanical energy acquires the following form:
 (8)
(8)
Now, by solely modifying the amplitude of the motion, denoted by zm, and by keeping the values of mass and pulsation constant, we obtain:
 (9)
(9)
Once fixed the value of zm, from Equations (1) and (9) we obtain:
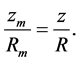 (10)
(10)
At any given time, the value of R is obviously univocally determined by means of Equation (1), being Rm a constant. On the contrary, the value of z, provided by Equation (9), depends on the amplitude of the motion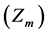 , that can vary between zero and Rm.
, that can vary between zero and Rm.
The total mechanical energy of a material point, whose motion is defined by Equation (9), acquires the following form:
 (11)
(11)
The material point can be replaced by a material segment (in other terms, it is as if we consider a spring, no longer ideal, whose length at rest is equal to Rm). The length (R) of the segment evolves in accordance to Equation (3). If we denote with M the mass of the segment, the linear density can be defined as follows:
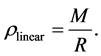 (12)
(12)
Denoting with Mz the mass of a portion of the segment, characterized, at any given time, by a length equal to z, we can write the following:
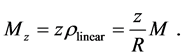 (13)
(13)
Taking into account Equations (11) and (13), the energy related to an infinitesimal material segment can be written as follows:
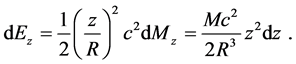 (14)
(14)
Therefore, the final expression for the energy of a material segment, whose length, at any given time, is equal to z, acquires the underlying form:
![]() (15)
(15)
2. Discussion
Let’s consider a 4-ball, centered at the origin, whose radius, denoted by R, evolves in accordance to Equation (1). The corresponding boundary, that represents the space we are allowed to perceive (when we are at rest), is a three dimensional surface (a hyper sphere) characterized by the following identity:
![]() (16)
(16)
The Universe in its entirety is described by the following inequality:
![]() (17)
(17)
Let’s consider the point
![]() (18)
(18)
and its antipode (the one diametrically opposite)
![]() (19)
(19)
Now, let’s consider the straight line segment bordered by the above mentioned points. Figure 2 provides a representation of this segment by looking into the scenarios that arise from Equation (17) when setting equal to zero, one at a time, all the four coordinates.
If we set![]() , we evidently obtain nothing but a single point. Therefore, let’s examine the three-dimensional scenarios that arise from the underlying identity:
, we evidently obtain nothing but a single point. Therefore, let’s examine the three-dimensional scenarios that arise from the underlying identity:
![]() (20)
(20)
For example, we can set ![]() (obviously, the same line of reasoning can be followed by setting
(obviously, the same line of reasoning can be followed by setting ![]() and
and![]() ). As a consequence, from Equations (17), (18) and (19), with obvious meaning of symbols and signs, we obtain the following:
). As a consequence, from Equations (17), (18) and (19), with obvious meaning of symbols and signs, we obtain the following:
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
Now, let’s consider the straight line segment bordered by the center of the ball and the point defined by Equation (22). If the segment in question, whose length evolves in accordance with Equation (1), is provided with a mass equal to M, its energy can be immediately deduced by Equation (15) by setting z = R. Consequently, underlining how the same procedure can be banally carried out by considering the point defined by Equation (23), we can write, with obvious meaning of notation, as follows:
![]() (24)
(24)
Generalizing the outcome just obtained, we can write:
![]() (25)
(25)
Therefore, for the material segment in its entirety, bordered by the points defined by Equations (22) and (23), characterized by a length equal to 2R and a mass equal to 2M, the energy is provided by the underlying relation:
![]() (26)
(26)
Finally, by superposition, we can easily write the total amount of energy related to the material segment bordered by the points defined by Equations (18) and (19) as follows:
![]() (27)
(27)
The points defined by Equations (18) and (19) are nothing but the interceptions between the material segment, whose energy is provided by Equation (27), and the hyper surface described by Equation (16). The latter represents the Universe we are allowed to perceive when we are at rest. As far as our perception of reality is concerned, each point and its antipode are to be actually considered as being the same thing, since they both belong to the same straight line segment [6] . On this subject, it is fundamental to underline how we could carry out a banal translation of the frame of reference, by setting the origin in correspondence of one of the endpoints of the material segment. In the light of what just declared, taking into account the symmetry, the scenarios that arise from Equation (20) may be represented as shown in Figure 3.
In other terms, we may state that the one provided by Equation (27) represents the total energy that can be ascribed to what we perceive as being a material point at rest.
To carry out an opportune rewriting of the conservation of energy principle, we have to suppose that the total amount of energy of a material segment must remain the same.
On this purpose, let’s generalize Equation (27). Firstly, we have to replace, in Equations (18) and (19), R with z. Now, if we take into account Equations (13) and (15), by following the procedure previously discussed, we can deduce, for one among the scenarios that arise from Equation (20), the energy that should be ascribed to a material segment characterized by a length equal to 2z and a mass equal to 2Mz. Finally, we can write, with obvious meaning of notation, the following:
![]() (28)
(28)
Let’s suppose that the above-mentioned material segment starts rotating around an orthogonal axis. If we denote with v the tangential speed of the endpoints, and with I the moment of inertia, we can write the correspondent kinetic energy as follows:
![]() (29)
(29)
The moment of inertia is banally provided by the following relation:
![]() (30)
(30)
From Equations (29) and (30) we immediately obtain:
![]() (31)
(31)
Taking into account Equations (26), (28) and (31), we may express the conservation of energy, for the considered scenario, as follows:
![]() (32)
(32)
By multiplying by three all the members of Equation (32), we immediately obtain the underlying noteworthy relation:
![]() (33)
(33)
As far as the last member of Equation (33) is concerned, we may state that the first term represents the kinetic energy, the second term, that could be in appropriately defined as the potential energy, represents an energetic amount evidently related to the curvature, while the third term represents the energy actually needed to produce the motion.
From Equation (33) we immediately obtain:
![]() (34)
(34)
From Equation (34) we can deduce the following fundamental relation:
![]() (35)
(35)
We can interpret Equation (35) as follows: if a point, or better what we perceive as being a point, starts moving with a constant speed equal to v, it is as if it were instantly dragged towards an inner surface characterized by a radius of curvature equal to z. Actually, as qualitatively shown in Figure 4, we should more properly state that any segment, whose endpoints start moving with a tangential speed equal to v, undergoes a radial contraction (and its mass undergoes a reduction that, as later discussed, we cannot perceive).
From Equation (35), if we introduce the so-called Lorentz factor [7] , we can write:
![]()
Figure 4. Radial contraction of a material segment.
![]() (36)
(36)
Fundamentally, summarizing the results up to now obtained, we may state that our perception of reality depends on the state of motion. Very simply, if we start moving with a constant speed equal to v, the Universe we are allowed to perceive is no longer represented by Equation (16), but rather by the following identity:
![]() (37)
(37)
Now, from Equations (13), (34) and (36), we immediately obtain:
![]() (38)
(38)
If we multiply the first and second members of Equation (38) by the Lorentz factor, taking into account Equation (27), we can write the following:
![]() (39)
(39)
From Equation (39), taking into account Equation (13) and (36), we obtain:
![]() (40)
(40)
Once fixed the mass at rest of the material segment (M), the energy provided by Equation (40) represents, obviously, a constant. On the contrary, the reduced mass (Mz) does not represent an invariant, since it evidently depends on the state of motion. Bearing in mind that, due to motion, the material segment undergoes a radial contraction, we can divide the energy by z, that is to be always considered as greater than zero. This way, we banally obtain the energetic density (in other terms, the amount of energy per length unit). The result can be multiplied by a length, denoted by l, that could be identified with the dimensional thickness (the thickness that can be ascribed to our three-dimensional curved space), so obtaining the following relation:
![]() (41)
(41)
![]() (42)
(42)
The one obtained in Equation (42) represents the energy that can be ascribed to a point characterized by a mass, that now can be considered as being a relativistic invariant, equal to m, that moves with a speed equal to v.
By following the same line of reasoning, bearing in mind that, net of the symmetry, the radial extension of the material segment at rest is to be considered as being equal to R, we can immediately deduce the expression for the so called energy at rest:
![]() (43)
(43)
From Equations (42) and (43) we can deduce the following well known relation:
![]() (44)
(44)
The one provided by Equation (44), usually identified with kinetic energy, actually represents the energy needed to produce the motion.
3. Conclusion
In this paper, starting from the well-known concept of oscillating Universe [1] some noteworthy relations, commonly defined as relativistic, have been deduced. We have hypothesized a closed Universe, globally flat, characterized by the existence of at least a further spatial dimension. Time has been supposed as being absolute. Under these hypothesis, taking for granted homogeneity and isotropy, we have elsewhere deduced [3] (by carrying out a noteworthy position on the gravitational constant, and by opportunely setting the parameter that appears in the equation of state suggested by Zeldovich [9] ) the so-called Friedmann-Lemaitre equation, with a null curvature parameter and a negative cosmological constant, without using Einstein’s Relativity. The concept of material point has been herein replaced by that of material line segment: in other terms, what we perceive as being a point may actually be a straight-line segment that crosses the centre of the four-dimensional ball that represents our Universe. Mass-en- ergy equivalence turns out to be nothing but the conservation of energy principle: In fact, we have started by postulating that the amount of energy that can be ascribed to whatever material segment is to be considered as being constant [2] . If speed tends to that of light, the so-called relativistic energy, whose writing is formally equivalent to the conventional one, tends to infinity. The reason is simple: motion produces a mass reduction, although the mass we perceive can be considered as an invariant. More precisely, real mass tends to zero when speed tends to that of light: As a consequence, specific energy tends to infinity. Obviously, the deformations of the spatial lattice induced by mass have been herein ignored: On this subject, it could be worth highlighting how we have elsewhere qualitatively discussed the hypothesis according to which gravity may not produce any time dilation [10] . It is fundamental to underline how the particular line of reasoning we have followed in order to obtain mass-energy equivalence requires, necessarily, that the Universe belongs to the oscillatory class. Obviously, the hypothesis that our Universe may oscillate represents anything but a novelty [11] : Starting from General Relativity, in fact, we can obtain static, asymptotic, monotonic, and oscillating models. The well-known problems related to some cyclic models [12] , such as the (apparent) singularity at t = 0 (we are herein referring to the O1 type in Harrison’s classification), have not been addressed in this paper. On this subject, we specify how the metric variation of cosmological distances is not considered as a real phenomenon: in other terms, the amount of space between whatever couple of points remains the same with the passing of time, and the Universe can be considered as being actually static. However, to thoroughly discuss the metric variation of cosmological distances (and, as a consequence, the interpretation of cosmological red shift), it would have been necessary to speculate about the real nature of radiation, as well as about the well-known problem related to dark energy: We can herein just declare that the total number of dimensions we would have had to hypothesize, net of the symmetry, should have been actually greater than four. Nonetheless, such a speculation would have led the discussion far beyond the aim of this paper. It is quite evident how all the equations we have obtained are formally identical to the ones that characterize Einstein’s Special Relativity: Nonetheless, it should be rather clear how their meaning is deeply different. The hypothesized absoluteness of time should immediately suggest how the aim of this paper does not consist in a mere deduction of equations, routinely classified as relativistic, surely well-known in literature. The equations arisen from Special and General relativity have proven to be able to effectively describe the phenomenological reality, but it does not necessarily mean that the above-mentioned theories are absolutely valid in their entirety, at least as far as their meaning is concerned. Relativistic time dilation, for example, is herein considered as being nothing but an apparent phenomenon: it may be simply related to the radial contractions of material segments, perceived as material points, induced by motion. For example, the alleged increase of the lifetime of muons, although coherent with Special Relativity, could be easily explained avoiding time dilations. Muons evidently succeed in covering a distance clearly not compatible with their mean lifetime: this is unconfutable. On the one hand, we could admit that time, for muons, starts slowing down due to the high value of their speed. On the other hand, and for the same reason, we could imagine that, for muons, the distances undergo a contraction. In the latter case, the speed perceived by an observer at rest is greater that the real one, but time does not undergo any dilation whatsoever. Two different explanations, one of which based upon the absoluteness of time, both fully compatible with the Lorentz Equations, that consequently, though, acquire a completely different meaning in the two cases [13] .