Modelling the Dynamical State of the Projected Primary and Secondary Intra-Solution-Particle Movement System of Efavirenz In-Vivo ()
1. Introduction
The intra-solution-particle movement system is described in this work. A system which consists of the primary and secondary movement states that is proposed in Nemaura (2015) is investigated. Differential Equations are used to describe dynamical systems. Most systems are described relative to time [1] [2] [3] . In this work, they are used to describe a dynamical system of the state of a solution particle relative to concentration.
Multiple compartmental modelling finds its use in fields such as Physiologically Based Pharmacokinetics, Engineering and Mathematical Biology [1] [3] [4] . Other researchers work with constant parameters that are obtained for autonomous linear systems. In this work, a simple system (nonautonomous linear system) whose parameters vary according to concentration is considered [5] [6] . The mixing problems have been widely studied by the use of ordinary differential equations [4] [7] [8] . Additionally, some researchers consider probable systems that arise from these mixing problems [7] [8] . This work proposes a system of linear ordinary differential equations that potentially govern the state of solution particle and shares a relation to the mixing problems. In addition, there is consideration of a volume conserving state of a solution particle. The dynamic eigenvalues from the corresponding matrix and stability of the concentration varying linear systems are proposed. The dynamic eigenvalues have found applications for linear time-varying systems [2] .
This work highlights possible intra-particle movement potential/states inferred to be present in the solution particle, at primary and secondary level and attempts to give mathematical form as in Nemaura (2015) [9] . It proposes multiple-compartmental models, one for the primary level and the other for the secondary level. The resultant form gives a general representation of movement within a solution particle.
2. Methods
The primary and secondary movement system of projected simulated data from patients who had been on efavirenz is used [9] . The software used, were R and Mathematica.
2.1. The Primary System
The primary system is a sub-system of the secondary and describes potential. It is projected to consist of four main movement entities that is convection, saturation, passive and advection. The form entity being the advective component [9] .
2.2. The Primary System of Solution Particle
A solution particle with concentration (x) is made up of four movement components (variables) at primary level C-convective, A-advective, P-Passive, and S-Saturation at primary level satisfying
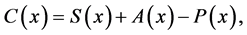 (1)
(1)
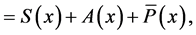 (2)
(2)
where 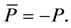
We analyse the following system of differential equations in order to infer on the overall process occuring in describing state of movement in a solution particle (See Figure 1).
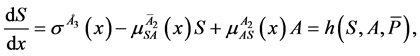 (3)
(3)
 (4)
(4)
 (5)
(5)
Subject to,
![]()
Figure 1. A compartmental representation of the model for solution particle movement state dynamics at primary level driven by the advective component. It is noted that this representation is not necessarily unique for all forms of advective component.

And
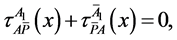
With 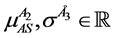
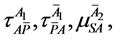 and are the variable parameters. These two conditions allows no net change in the volumetric consituencies of the four movement components, where
and are the variable parameters. These two conditions allows no net change in the volumetric consituencies of the four movement components, where
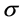 ―single phase third generation solution sub-particle at primary level, form inducing movement interaction with four main movement entities,
―single phase third generation solution sub-particle at primary level, form inducing movement interaction with four main movement entities,
 ―single phase second generation solution sub-particle at primary level with four main movement entities, and
―single phase second generation solution sub-particle at primary level with four main movement entities, and
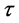 ―altering phase(s) first generation solution sub-particle at primary level with three main movement entities.
―altering phase(s) first generation solution sub-particle at primary level with three main movement entities.
Solving the primary system above (1 - 5) in terms of advective components,
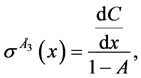
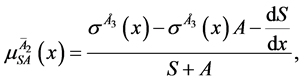
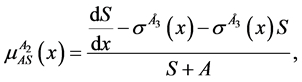
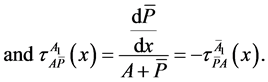
2.3. Stability Analysis of the Primary System
The equlibrium, steady state points are constant solutions, ![]() , and
, and ![]()
which satisfy the nonlinear system of equations ![]() and
and ![]() These
These
points govern the behaviour of physical models. Thus we obtain ![]() (form potential),
(form potential), ![]() (space accesory potential), and
(space accesory potential), and ![]() (negative binding-orientation potential). It is important to note that the convective potential at equilibrium (primary level) is negative (nullifying/compensating accesory potential). Furthermore, it has the value of −1.
(negative binding-orientation potential). It is important to note that the convective potential at equilibrium (primary level) is negative (nullifying/compensating accesory potential). Furthermore, it has the value of −1.
Local Analysis near Steady-State Points ![]()
Local analysis is studied near each steady state point![]() . We begin by the following,
. We begin by the following,
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
where![]() ,
, ![]() and
and ![]() are small.
are small.
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
The partial derivatives are evaluated at the equilibrium point![]() . The stability of the steady state point
. The stability of the steady state point ![]() is investigated by studying the eigenvalues of the Jacobian matrix (A matrix of the partial derivatives). The Jacobian matrix for the primary system is given by,
is investigated by studying the eigenvalues of the Jacobian matrix (A matrix of the partial derivatives). The Jacobian matrix for the primary system is given by,
![]() (12)
(12)
(I)Undisturbed potential![]() ,
, ![]() where
where
![]() . The characteristic equation of J is given by,
. The characteristic equation of J is given by,
![]()
Eigenvalues of this system are given by,![]() . The equilibrium point has neutral stability. Thus the primary unique space interacting potential has a neutral equilibrium before “disturbances”.
. The equilibrium point has neutral stability. Thus the primary unique space interacting potential has a neutral equilibrium before “disturbances”.
(II) Disturbed (dissolving) potential![]() ,
, ![]()
The dynamic eigenvalues follows from the characteristic equation of J given by,
![]()
which is similar,
![]()
![]()
Thus the eigenvalues for this system are,
![]()
![]()
And
![]()
where![]() , and
, and
![]()
(III) Saturated potential (![]() :
:![]() ,
, ![]() ,
, ![]() ). The characteristic equation is given by,
). The characteristic equation is given by,
![]()
2.4. The Secondary System of Solution Particle
The product of advective primary interaction potential with its unique space (the relative uptake) results in a secondary advective movement system [9] . A solution particle with concentration (x) is made up of three movement components (variables) at secondary level![]() ―convective,
―convective,![]() ―advective, and
―advective, and![]() ―Saturation at secondary level satisfying
―Saturation at secondary level satisfying
![]() (13)
(13)
This is represented by the following constituent system (See Figure 2),
![]() (14)
(14)
![]() (15)
(15)
Subject to,
![]()
With ![]() (variable parameters). The condition allows no net change in the volumetric consituents of the movement components. Where,
(variable parameters). The condition allows no net change in the volumetric consituents of the movement components. Where,
![]() ―single phase third generation solution sub-particle at secondary level, form
―single phase third generation solution sub-particle at secondary level, form
![]()
Figure 2. A compartmental representation of the model for solution particle movement state dynamics at secondary level driven by the advective component.
inducing movement interaction with four main movement entities,
![]() ―single phase second generation solution sub-particle at secondary level with four main movement entities.
―single phase second generation solution sub-particle at secondary level with four main movement entities.
Solving the secondary system above (13) - (15),
![]()
![]()
![]()
2.5. Stability Analysis of the Secondary System
The equlibrium, steady state points are constant solutions, ![]() and
and![]() , which
, which
satisfy the nonlinear system of equations ![]() and
and![]() . It is shown that this
. It is shown that this
system is orbitally stable, which signifies that the solutions remain near the equilibrium point.
Local Analysis near Steady-State Points ![]()
Considering,
![]()
![]()
Thus we obtain, ![]() (form state), and
(form state), and ![]()
(space accessory state). It is important to note that the convective movement at secondary level is a stable state which is 0 (nullifying/stabilising accessory state). We study local analysis near each steady state point ![]() for Equations (14) & (15). We begin by the following,
for Equations (14) & (15). We begin by the following,
![]() (16)
(16)
![]() (17)
(17)
where ![]() and
and ![]() are small. Next we substitute Equations (16) & (17) into (18) & (19).
are small. Next we substitute Equations (16) & (17) into (18) & (19).
![]() (18)
(18)
![]() (19)
(19)
The Jacobian matrix for the secondary system is given by,
![]() (20)
(20)
The eigenvalues ![]() and
and ![]() for this system are given by
for this system are given by ![]() and
and
![]() respectively. The secondary system gives a form of neutral stability.
respectively. The secondary system gives a form of neutral stability.
3. Results
3.1. Numerical Projections of Sub-Particle and Particle of Solution for the Primary System
The graphical representation of the advective components ![]() (sub-systems) are shown (see Figure 3). The solution is developed from the primary system equation in Nemaura (2015) and the system (1 - 5).
(sub-systems) are shown (see Figure 3). The solution is developed from the primary system equation in Nemaura (2015) and the system (1 - 5).
The primary system and sub-system equations and estimated parameters are given (See Equations (21) - (27) and Table 1).
Primary system equation,
![]() (21)
(21)
Primary![]() ―sub-particle equation given by,
―sub-particle equation given by,
![]() (22)
(22)
Primary![]() ―sub-particle equation given by,
―sub-particle equation given by,
![]() (23)
(23)
![]()
![]()
Table 1. Parameter estimates in modelling movement rates associated with the primary system.
Primary![]() ―sub-particle equation given by,
―sub-particle equation given by,
![]() (24)
(24)
Primary![]() ―sub-particle
―sub-particle ![]() equation given by,
equation given by,
![]() (25)
(25)
where ![]()
Primary![]() ―sub-particle
―sub-particle ![]() equation given by,
equation given by,
![]() (26)
(26)
Primary![]() ―sub-particle
―sub-particle ![]() equation given by,
equation given by,
![]() (27)
(27)
where ![]() is the point when the system is projected to show considerable loss of homogeneity-potential.
is the point when the system is projected to show considerable loss of homogeneity-potential.
Furthermore, ![]()
3.2. Numerical Projections of Sub-Particle and Particle of Solution Movement for the Secondary System
The graphical representation of the advective components ![]() (sub-systems) are shown (see Figure 4). The solution is developed from the secondary system equation in Nemaura (2015) and the system (13 - 15).
(sub-systems) are shown (see Figure 4). The solution is developed from the secondary system equation in Nemaura (2015) and the system (13 - 15).
The secondary system and sub-system equations and estimated parameters are given (See Equations (28) - (31) and Table 2). Secondary system equation is given by,
![]() (28)
(28)
Secondary![]() ―sub-particle equation given by,
―sub-particle equation given by,
![]() (29)
(29)
Secondary![]() ―sub-particle equation given by,
―sub-particle equation given by,
![]() (30)
(30)
Secondary![]() ―sub-particle equation given by,
―sub-particle equation given by,
![]() (31)
(31)
3.3. Stability Numerical Analysis for Secondary System
Let ![]() and the plot of
and the plot of ![]() against x is given (See Figure 5). The results show that
against x is given (See Figure 5). The results show that ![]() for almost all values of concentration (x). The following is proposed
for almost all values of concentration (x). The following is proposed ![]() where
where ![]() is the error term in estimating
is the error term in estimating
![]()
Table 2. Parameter estimates in modelling movement rates associated with the secondary system.
![]()
Figure 5. The value p of the characteristic equation against concentration x.
![]() . The system is inferred to be stable.
. The system is inferred to be stable.
4. Discussion
A nonautonomous linear system is developed that enables characterisation of the projected movement in a solution-particle [5] [6] . There are four main movement potential components at primary level with respect to advection. They are held together by the sub-system also a potential which is inferred to have five distinct systems (that is the two![]() , s and two
, s and two![]() ). While, the secondary system consists of two
). While, the secondary system consists of two ![]() and s. The variable parameters in the system of ordinary differential equations are inferred to describe (advective) form components of movement. The movement description gives the state of solution particle and there is suggestion of the constituent entities.
and s. The variable parameters in the system of ordinary differential equations are inferred to describe (advective) form components of movement. The movement description gives the state of solution particle and there is suggestion of the constituent entities.
The primary system is generally projected to be an unstable system relative to concentration. The saturated system is inferred to have stable potential. The reaction allowing state (non-saturated concentration) has unstable equilibrium potential at primary level. However, the secondary system is stable.
This work has managed to describe the possible state of kinetics of a solution-particle of efavirenz. It has shown that a saturated state can be equated to a stable state both at primary and secondary level. The constructed matrix in this case is traceless that is it has zero trace. The volume conserving systems have been considered in modelling of the physical systems and the theoretical framework is also developed in Lie Theory [10] [11] .
Acknowledgements
The author would like to thank the following; C. Nhachi, C. Masimirembwa, and G. Kadzirange, AIBST and The College of Health Sciences, University of Zimbabwe.