1. Introduction
Since its introduction, the iterative threshold decoding algorithm (ITDA) [1] of one step majority logic decodable codes has gained great interest [2] [3] [4] and this is for several reasons. In fact, OSMLD codes are a subclass of LDPC codes currently present in most telecoms standards, but can be decoded iteratively by ITDA which is less complex than belief propagation algorithm with approximatively the same performances. Getting the performance of these codes is carried out by simulation to evaluate the evolution of the BER compared to the SNR. However, this operation is very expensive in terms of time, especially for long codes. To address this problem, different techniques have been proposed in the literature to analyze the iterative decoding of concatenated codes [5] [6] [7] . The most used method is based on mutual information known as the Exit (Extrinsic Information Transfer) Chart. Indeed, it has been shown by simulation (case of a frame of large size) [8] that the model used by the extrinsic exchanged between the decoders is Gaussian. Moreover, the study of a single decoder is sufficient to predict the iterative decoding performances.
All work on the Exit chart have focused around the iterative decoding of convolution codes, however, in this paper, we propose to apply it to analyze the convergence behavior of the iterative decoding threshold of one step majority decodable codes. Our work is distinguished by the fact that the codes used are structural block codes completely different from that of convolutional codes and that are decoded by our iterative decoding algorithm [1] [2] .
The organization of this article is as follows: Section 2 describes the iterative threshold decoding process. In Section 3, we begin with the presentation of the principle of calculating the Exit Chart and end with behavior analysis of convergence of ITDA when applied in both simple and concatenated OSMLD codes. Section 4 provides some conclusions.
2. Iterative Threshold Decoding Process
In this section a brief description of our proposed iterative decoding algorithm [1] will be given. We will focus in particular on variables that will serve us for the calculation in the Exit chart.
2.1. Soft-In Soft-Out Threshold Decoder
First, Let us consider a transmission of code word C (n, k, d) of binary symbols {0, 1} using a BPSK modulation over AWGN channel, the decoder soft output for the jth bit position of a given soft input R (r1, r2 ・・・ rn) is defined as:
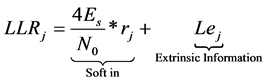 (1)
(1)
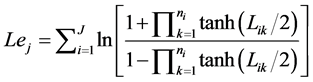 (2)
(2)
where J is the number of orthogonal parity check equations in code C, ni represents the number of elements in the ith orthogonal equation, ik represents the kth element of the ith
parity check equation orthogonal to the jth bit and .
.
The computation of extrinsic information can be approximated by replacing the formula (2) by:
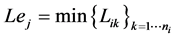 (3)
(3)
Which is a good approximation since it requires only signal adders and comparators and can be most easily implemented without undue deterioration in error performance.
The algorithmic structure of the SISO threshold decoding can be summarized as follows:
For each bit 
Compute the extrinsic information Lej as (3)
Compute the Soft-input
Compute de Soft-output: LLRj = (4Es/N0) rj + Lej
Correct de bit rj
Table 1 shows some examples of OSMLD codes that can be decoded by theses codes are also known as self orthogonal codes. In this table we used the abbreviations DSC for Difference Set Cyclic codes, EG for Euclidean Geometry codes and BCH for Bose Chaudhuri and Hocquenghem codes. For an extensive description of projective geometry codes and Euclidean geometry can be found in [9] .
2.2. Iterative Threshold Decoding Process
The Iterative decoding process (see Figure 1) can be described as follows: In the first iteration, the decoder only uses the channel output as input, and generates extrinsic information for each symbol. In subsequent iterations, a combination of extrinsic information and channel output is used as input.
The soft input respectively the soft output of the qth iteration is given by:
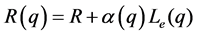 (4)
(4)
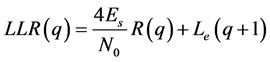 (5)
(5)
where R represent the received data, Le(q) is the extrinsic information computed by the previous iteration. In our procedure we use a fixed value 1/J for the pparameter 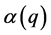 and this for all iterations. The value chosen for
and this for all iterations. The value chosen for  reacts as if one took an average of all J estimators which contribute in the computation of Le.
reacts as if one took an average of all J estimators which contribute in the computation of Le.
Our iterative decoding process can also be applied to the concatenated codes; in this case R is a matrix whose rows are constructed from the C1 code and columns from C2
code. Extrinsic information computed by the SISO decoder of code C1 is given as a priori information to the second SISO decoder of code C2. Table 2 shows some code built from the concatenation of OSMLD codes.
We wish to emphasize that our algorithm can be applied to simple majority decoding codes, product codes (PC) or parallel (PCB) [2] , serial concatenated codes [4] and quasi-cyclic codes [3] . Indeed in [10] we showed that our algorithm has a good compromise between complexity and performance compared to the belief propagation algorithm (BP). For example, for the code DSC (273, 191) our algorithm is 5 times faster than BP. Figure 2 depicts the performance of iterative decoding of (1057, 813) DSC code with rate 0.69 on AWGN channel. We can see that the performance improves with each iteration and no improvement after 15th iteration, at this stage we can said that the decoding process has converged. The number of iterations for convergence as well as the SNR at which begins the enhancement (Point of separation of the different curves) will be predicted by the Exit chart.
3. Convergence Behavior Analysis
3.1. Exit Chart Computation
EXIT chart [5] [6] [7] [8] has emerged as a useful tool for analyzing convergence behavior of iterative decoding of both Turbo codes and LDPC codes. Theses diagrams propose a graphic visualization of the evolution of the quality of the extrinsic information exchanged between two SISO decoders (Turbo codes) or between variable nodes and check nodes in case of LDPC codes. We succeed to apply EXIT charts technique to our
![]()
Figure 1. The block diagram of the qth iteration.
![]()
Table 2. Set of concatenated codes.
iterative decoding process while only one SISO decoder is used. The evolution of extrinsic information at the output of our SISO decoder is visualized during iterations. Figure 3 represents the simulation model to be implemented for calculation of EXIT chart. Let X denote the binary input to an additive white Gaussian noise AWGN channel, X = {±1}, and LCH its corresponding output expressed as a log-likelihood ratio LLR. The soft-input/soft-output (SISO) decoder receives as its input both LCH and a priori information LA, which is also expressed as a LLR.
For purposes of the analysis, it is assumed that the sequences {LA} and {LCH} at the input to the decoder are infinitely long. One can easily show that { LCH } Gaussian (conditioned on X) with parameters (2/s², 4/s²) where s² = N0/2Es. Under the assumption that the a priori LLR {LA} follows a Gaussian distribution we have  where
where 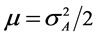 and h are a Gaussian variable of zero mean and variance
and h are a Gaussian variable of zero mean and variance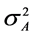 . The mutual information IA = I (X; A) between X and A which can be expressed as:
. The mutual information IA = I (X; A) between X and A which can be expressed as:
 (6)
(6)
![]()
Figure 2. BER performance of (1057, 813) code on AWGN channel.
We put
![]() (7)
(7)
where ![]() and
and![]() . The function J is monotonically increasing and can be calculated numerically only once because J and J−1 are the same for all codes.
. The function J is monotonically increasing and can be calculated numerically only once because J and J−1 are the same for all codes.
On the other hand the mutual information between the extrinsic LLR of the IE and X, IE = I (X; E) can be expressed as:
On the other hand the mutual information between the extrinsic LLR of the IE and X, IE = I (X; E) can be expressed as:
![]() (8)
(8)
It is impossible to express this relation in analytical form; the distributions pE is most conveniently determined by means of Monte Carlo simulation. Viewing IE as a function of IA and the signal to noise ratio SNR value, the extrinsic information transfer characteristics is defined as:
![]() (9)
(9)
For a concatenated constructed from C1 (n1, k1) and C2 (n2, k2) and a fixed SNR, the different steps of calculation can be summarized as follow:
Initialize a word w of size (k1 × k2) with bit 0
Initialize the maximum of iteration at Max
Modulate w with Binary phase shift key (BPSK)
Transmit de code word over an AWGN channel
Do
Generate LA for columns (AWGN/sA) and compute IA
Decode Lines of the received word and compute IE
sA = sA + (sA/Max)
Iteration = Iteration + 1
While (iteration! = Max)
3.2. Convergence Analysis of ITD
In order to guarantee a good approximation of the graphical output, it is convenient to work with blocks of size of the order of 105. However, the approximation of the distribution of LE by a Gaussian variable is checked in the case of finite length codes (Figure 4). This assumption will allow us to validate curves Exits reports rated to the BER curves.
Figure 4 shows the evolution of the distribution of the extrinsic information at the output of the SISO threshold decoder of PC code (74529, 36481). We simulated the transmission of a frame without any approximation.
Transfer characteristics ![]() for different SNR are shown in Figure 5. The a priori input IA is on the abscissa, the extrinsic output IE is on the ordinate. The SISO threshold decoding algorithm is applied to (819, 447) OSMLD code of rate 0.54. The numbers on different curves are the SNR values in dB. The obtained diagrams look like those of Turbo code.
for different SNR are shown in Figure 5. The a priori input IA is on the abscissa, the extrinsic output IE is on the ordinate. The SISO threshold decoding algorithm is applied to (819, 447) OSMLD code of rate 0.54. The numbers on different curves are the SNR values in dB. The obtained diagrams look like those of Turbo code.
![]()
Figure 4. Evolution of the distribution of the extrinsic LE based on iterations.
![]()
Figure 5. Extrinsic information transfer characteristics of SISO decoder for code (819, 447) on AWGN channel.
To view the convergence behavior of the iterative decoding, we draw in the same figure (see Figure 6) the exit charts of the two decoders. In the case of a symmetrical concatenated code the curve of the second decoder is obtained by inverting the symmetry axis of the IE and IA.
Figure 6 depicts the Exit chart of the concatenated code PC (74529, 36481) constructed from DSC (273, 191) for SNR 2.5, 3, 3.15 and 3.5 dB. The expected decoding trajectory is the “stairs”-like and can be explained as follows: Let q be the iteration index. For q = 0 the decoding process starts at the origin with zero a priori knowledge IA,0 = 0. At iteration q, the extrinsic output IE,q = T (IA,q) is forwarded as a priori knowledge for the next decoder IA,q+1 = IE,q, and so on, until IA = IE = 1 after about 16 iterations. Each step of the staircase curve represents one iteration of the decoding process.
Figure 7 shows the Exit chart curve for iterative decoding of asymmetric concatenated code constructed from DSC (273, 191) and DSC (73, 45) at SNR 2.8 dB. In this case and contrary to the result obtained in the figure 6 we calculated and plotted the transfer curves for each Component elementary decoder. As we can see both transfer curves enters a tunnel at SNR = 2 dB away from the x = y − axis.
![]()
Figure 6. Exit charts of PC code (74529, 36481) and decoding trajectory on a Gaussian channel.
![]()
Figure 7. Exit charts of asymmetric concatenated code (19929, 8595) at SNR = 2.8 dB.
BER chart vs. Exit chart
Two main regions can be defined from the curve of BER (see Figure 8). The first is called “pinch-off Region” (for SNR < 2.9 dB) whose BER remains constant and iteration has no effect. The second is called “waterfall Region” (SNR > 2.9 dB) here, the BER decreases excessively when the rate increases SNR. These three regions can be illustrated using the exit chart (see Figure 6).
“Pinch-off Region” the two decoders transfer curves cross at small values of mutual information (no convergence).
“Waterfall Region”: the decoding trajectory enters a tunnel area [5] near the bisector with a slower convergence rate.
For SNR = 3.15 dB we can observe that the decoding trajectory enters an area of tunnel close to the x = y − axis with a deceleration characteristic of convergence’s speed. The bit error rate (BER) versus SNR performance on AWGN channel is displayed in Figure 8. As we can observe, the waterfall region appears to take shape at SNR > 2.9 dB, which is 0.25 dB away from Exit chart threshold. This uncertainty of estimate is due mainly to the fact that we use a code with finite length.
4. Conclusion
In this work, we applied Exit chart as a semi analytic method to predict convergence behavior of our iterative threshold decoding for simple and concatenated OSMLD codes with medium length and a gap of 0.3 dB was found compared to BER chart. This uncertainty of estimate is due mainly to the fact that we use a code with finite length.
The great interest of Exit chart is mainly due to the time we gain compared to the simulation based on BER. Indeed if we assume that θ is the decoding time of one frame
![]()
Figure 8. BER performances of ITD of PC code (74529, 36481) on a Gaussian channel.
and frame it takes to generate the BER is 1000, then the gain is of the order of 1000 × θ. As future work, we plan to apply the Exit on a concatenation of OSMLD codes with a convolutional code of rate 1, but also we believe that the Exit Chart can be applied to other non-linear iterative process such as that used in learning neural network.