Feasibility of Estimating Patient-Specific Dose Verification Results Directly from Linear Accelerator Log Files in Volumetric Modulated Arc Therapy ()
1. Introduction
Volumetric modulated arc therapy (VMAT) is a high precision beam delivery technique that dynamically varies multi-leaf collimator (MLC) leaf positions and dose rates during gantry rotation on a linear accelerator (linac) [1] . Because of this complexity, patient-specific quality assurance (QA) was routinely performed by comparing measured and calculated dose distributions inside a phantom, where the dose distributions were measured by a film, an ionization chamber [2] or a detector array [3] [4] .
Several groups previously reported VMAT plan complexity indices by referring to each treatment plan file [5] [6] ; however, the correlation between the complexity indices and the dose QA results was relatively weak. In these papers, the complexity indices were calculated by the leaf aperture in each control point written in each treatment plan file, thereby unable to reflect the machine control errors of the gantry and the MLC positions during VMAT delivery.
Tyagi et al. reported the correlation between MU-weighted integral field aperture errors and dose errors in a target and organs at risk, where the integral field aperture errors were calculated by comparing planned and measured field apertures by way of linac mechanical data monitoring whereas the dose errors were calculated by comparing planned and reconstructed doses [7] . However, the correlation was not clearly demonstrated in the scatter plots. Pasler et al. showed correlations between mean gamma values and MLC leaf errors for each control point of VMAT delivery using the linac log files [8] . However, this was instantaneous correlation during VMAT delivery and not for prediction of patient-specific dose verification results.
Previous reports mainly focused on field aperture or leaf position errors and few papers investigated correlation between gantry angle errors and the dose verification results. For example, Agnew et al. reported that the correlations between the gantry angle errors and the dose accuracy were not observed [9] . In this paper, VMAT delivery accuracy has been more extensively investigated by calculating the linac dynamic parameters consisting of control errors, speeds and accelerations of gantry angles and MLC leaf positions using log files. The purpose of this study is to predict the patient-specific dose verification results directly from the linac dynamic parameters, thereby simplifying the patient-specific dose QA procedure.
2. Materials and Methods
2.1. Patient Selection
Twenty-six prostate cancer patients who underwent VMAT in our institute were retrospectively and consecutively selected. Computer tomography (CT) imaging with a slice thickness of 2 mm was performed in supine position with a full bladder. This study was approved by the institutional review board.
2.2. Treatment Planning
Gross tumor volume (GTV) consisted of the entire prostate and the seminal vesicles. Clinical target volume (CTV) was identical to the GTV. Planning target volume (PTV) was defined by adding a margin of 10 mm to the CTV in all directions, except a posterior margin of 5 mm. Rectum, bladder, small bowel and large bowel were contoured as organs at risk.
VMAT plans were created by Monaco v.3.3 treatment planning system (TPS) (Elekta AB, Stockholm, Sweden) using a 10 MV photon beam. All VMAT plans consisted of a single clockwise full arc. A dose of 76 Gy in 38 fractions was prescribed to the 95% volume of the PTV excluding rectum overlap. A grid size of 3 mm was selected for the Monaco Monte Carlo dose calculation.
2.3. Linear Accelerator
A Synergy linac (Elekta AB, Stockholm, Sweden) equipped with an MLC with a leaf width of 1 cm was employed. The maximum gantry speed was 6 degree/sec, and the maximum leaf speed was 2 cm/sec. The dose rate was variable by a factor of two in six steps.
2.4. Log File Analyses
The VMAT plans were delivered in service mode, and gantry angles and MLC leaf positions along with cumulative monitor units (MU) and dose rates were recorded in log files with a sampling interval of 250 msec. The log file data were analyzed using an in-house software created by Visual Basic 2010 (Microsoft, Redmond, USA), resulting in control errors, speeds, and accelerations of the gantry angle and the MLC leaf positions in every 250 msec, based on the following equations where i denotes the current sample number:
 (1)
(1)
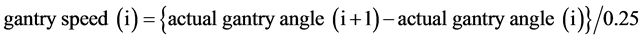 (2)
(2)
 (3)
(3)
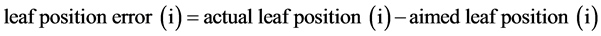 (4)
(4)
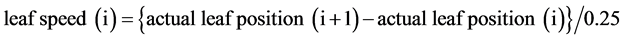 (5)
(5)
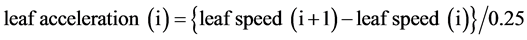 (6)
(6)
To simplify the above leaf parameter calculation, only central six leaf pairs that may cover the prostate PTV were considered.
2.5. Dose Verification
A cylindrical phantom with an array detector, ArcCHECK (Sun Nuclear Corp., FL) was used to verify the patient-specific delivery accuracy. The ArcCHECK has 1386 diodes with a measurement diameter of 21 cm. All treatment plans were transferred to the phantom for dose recalculation in Monaco. Gamma index pass rates between the calculated and the measured dose distributions were evaluated under two different criteria of 3%/3 mm and 2%/2 mm with a dose threshold of 10%.
2.6. Correlation Coefficient
A root mean square (rms) value of each parameter during each VMAT delivery was calculated. Subsequently, Pearson’s correlation coefficients (r) between gamma index pass rates and each of the above rms values were calculated by SPSS v.19 (IBM, New York, U.S.A.). Statistical significance was defined as a p value of <0.05.
3. Results
Table 1 shows the statistics of rms values of control errors, speed, and accelerations of the gantry angle and the leaf positions for all the VMAT deliveries.
Table 2 shows the statistics of the gamma index pass rates between the calculated and the measured dose distributions under the criteria of 3%/3 mm and 2%/2 mm with a dose threshold of 10% using the ArcCHECK.
Figure 1 shows scatter plots of the gamma index pass rates under 2%/2 mm criteria against the rms of a) leaf position error, b) leaf speed, c) leaf acceleration. Again, the pass rates were calculated under a dose threshold of 10% by comparing measured dose distributions using ArcCHECK and calculated dose distributions using Monaco TPS.
Figure 2 shows scatter plots of the gamma index pass rates under 2%/2 mm criteria against the rms of a) gantry angle error, b) gantry speed, c) gantry acceleration. The pass rates were calculated under a dose threshold of 10% by comparing measured dose distributions using ArcCHECK and calculated dose distributions using Monaco TPS.
Figure 3 shows scatter plots of a) the rms gantry speed against the rms gantry angle
![]()
Table 1. Statistics of rms controlled errors, speeds and accelerations of the leaf positions and the gantry angle for all the VMAT deliveries.
Abbreviation: SD = standard deviation.
![]()
Table 2. Gamma index pass rates between the calculated and the measured dose distributions under the criteria of 3%/3 mm and 2%/2 mm with a dose threshold of 10%.
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figure 1. Scatter plots of the gamma index pass rates under 2%/2 mm criteria against the root mean square (rms) of (a) leaf position error, (b) leaf speed, (c) leaf acceleration. No significant correlation was observed between the gamma index pass rates and each rms of the parameters related to MLC.
error, and b) the rms gantry acceleration against the rms gantry angle error. These parameters were calculated using a log file recorded during VMAT delivery. The correla-
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figure 2. Scatter plots of the gamma index pass rates under 2%/2 mm criteria against the rms of (a) gantry angle error, (b) gantry speed, (c) gantry acceleration. Significant correlation was observed between the gamma index pass rates and each rms of the gantry angle errors and the gantry accelerations (p < 0.001), whereas no significant correlation was shown between the gamma index pass rates and the rms gantry speed.
![]() (a)
(a)![]() (b)
(b)
Figure 3. Scatter plots of (a) the rms gantry speed against the rms gantry angle error and (b) the rms gantry acceleration against the rms gantry angle error. Both parameters were calculated by using a log file which was recorded during VMAT delivery.
tion coefficients of the rms gantry angle error versus each of the rms gantry speed and the rms gantry acceleration were 0.74, 0.66 respectively. Significant positive correlations were observed.
Table 3 shows correlation coefficients between the gamma index pass rates and each rms value of gantry angle error, gantry speed, gantry acceleration, leaf position error, leaf speed and leaf acceleration under the criteria of 3%/3 mm and 2%/2 mm. The correlation coefficients between the gamma index pass rates and the rms gantry angle errors were −0.49 (p = 0.011) under 3%/3 mm criteria and −0.64 (p < 0.001) under 2%/2 mm criteria, respectively. The correlation coefficients between the gamma index pass rates and the rms gantry speeds were −0.18 (p = 0.374) under 3%/3mm criteria and −0.36 (p = 0.069) under 2%/2 mm criteria, respectively. The correlation coefficients between the gamma index pass rates and the rms gantry accelerations were −0.47 (p = 0.017) under 3%/3 mm criteria and −0.68 (p < 0.001) under 2%/2 mm criteria, respectively. Significant negative correlations were observed between the gamma index pass rates and each of the rms values of the gantry angle errors and the gantry accelera-
![]()
Table 3. Correlation coefficients, r, between the gamma index pass rates and each rms of the leaf position error, the leaf speed, the leaf acceleration, the gantry angle error, the gantry speed and the gantry acceleration under the criteria of 3%/3 mm and 2%/2 mm. A probability of p < 0.05 was considered statistically significant.
tion. The correlation became stronger for stricter gamma index criteria of 2%/2 mm. On the other hand, other dynamic machine parameters related to the MLC did not significantly correlated with the gamma index pass rates.
4. Discussions
In this study, we investigated the correlation between the gamma index pass rate and each rms of leaf position errors, leaf speeds and leaf accelerations. The scatter plots in Figure 1 indicated no significant correlations between the gamma index pass rates under 2%/2 mm criteria and each rms value of the leaf position errors, leaf speeds and leaf accelerations. Again, Table 2 also supported this observation by the calculated correlation coefficients. Agnew et al. observed a strong correlation between the leaf position errors and the leaf speeds, while no correlation between the leaf position errors and the gamma results [9] . Agnew’s latter findings agree with our data, suggesting no major differences of dosimetric impact between Varian and Elekta MLCs for prostate VMAT cases.
We also investigated the correlation between the gamma index pass rates and each rms of the gantry angle errors, the gantry speeds and the gantry accelerations. It was demonstrated in Figure 2(a) and Figure 2(c) that each rms of the gantry angle errors and the gantry accelerations significantly correlated with the gamma index pass rates under 2%/2 mm criteria. Table 2 also supported this observation by the calculated correlation coefficients. However, these results do not agree with Agnew’s data [9] , reporting that the average and standard deviation of gantry angle errors were not related to the gamma index pass rates. This discrepancy may be explained by the fact that Agnew’s data was based on Varian RapidArc having a different VMAT control algorithm, where the gantry speed was maintained constant or slowly varied under continuously varying dose rate [10] . Agnew et al. investigated 10 prostate cases, showing that the average gantry angle errors were 0.025˚ ± 0.006˚, which is much less than our data given in Figure 2. In our Elekta VMAT, the dose rate varies by a factor of two in six steps and intensity modulation is effectively achieved by changing the gantry speed more rapidly, possibly leading to larger gantry acceleration and at the same time larger gantry angle errors.
We also demonstrated in Figure 3 that each rms of gantry speeds and gantry accelerations correlated with the rms gantry angle errors. Miura et al. reported a strong correlation between the rms gantry angle error and the rms gantry acceleration during VMAT delivery for maxillary cancer [11] . Our observation is in agreement with this report. Besides, Figure 2(b) showed that the rms gantry speed did not correlate with the gamma index pass rates under 2%/2 mm criteria. Having observed the narrow range of the rms gantry speeds in Figure 2(b), the above insignificant correlation may imply that the rms gantry speed is not a suitable parameter to estimate the gamma index pass rate.
The purpose of this study was to pursue the feasibility of estimating patient-specific dose verification results directly from linac log files. Figure 4 shows cubic polynomial
![]() (a)
(a)![]() (b)
(b)
Figure 4. Cubic polynomial curve fitting to the plots of (a) the gamma index pass rates against the rms gantry angle error and (b) the gamma index pass rates against the gantry acceleration given in Figure 2. A moving standard deviation, σ, was also calculated using three adjacent data for each plot and an interval of ±2σ was drawn above and below the fitting curve.
curve fitting to the plots of a) the gamma index pass rates against the rms gantry angle error and b) the gamma index pass rates against the gantry acceleration, both given in Figure 2. A moving standard deviation, σ, was also calculated using three adjacent data for each plot and gradually increasing intervals of 2σ above and below the fitting curve were drawn as 95% confidence intervals. It may be trivial that the gamma index pass rates do not follow a normal distribution because the maximum pass rate is bounded by 100%. However in this study the 95% confidence interval was calculated by assuming a normal distribution for the pass rate. It was shown in Figure 4(a) and Figure 4(b) when the rms gantry angle error or the rms gantry acceleration increased, the gamma index pass rates gradually fell down while increasing the variations. For example, if the rms gantry acceleration is 6 degree/sec2, the 95% confidence interval for the gamma passing rate may be between 97.0% and 99.6%; on the other hand, if the rms gantry acceleration is 12 degree/sec2, the 95% confidence interval may be between 90.6% and 100%. A possible cause of the larger variations in the gamma index pass rates may be that the impact of a given large rms gantry angle error on dose distributions depends on treatment plans, whereas the doses were always evaluated at the same detector positions.
The present study shows a possibility of estimating gamma index pass rates from dynamic parameters by analyzing the linac log files acquired during VMAT delivery. It was reported that log file analysis should not be solely relied upon for QA as it does not detect systematic machine errors resulting from incomplete calibration [8] [12] . Nevertheless, the log file-based patient-specific QA is advantageous because the QA procedure is less time consuming without phantom positioning errors.
Our study was performed under binned dose rate control, where the dose rate varied by a factor of two in six steps due to an earlier linac system design. Because the dose rate is not continuously variable, the gantry speed needs to be extensively varied in order to meet the MU/degree prescribed in the treatment plan thereby possibly resulting in frequent gantry acceleration and deceleration. A more recent linac controller system allows continuously variable dose rate in 256 steps [13] , where the continuously variable dose rate control system showed larger standard deviations of the gantry errors compared to the previous system. This may imply that the correlation between the gantry angle error and the gamma pass rate could be more significant for VMAT under continuously variable dose rate control.
A limitation of this study lies in that only prostate VMAT plans were examined. Evaluation for other tumor sites may allow us to analyze the linac dynamic parameters more extensively, thereby possibly resulting in more comprehensive perspective.
5. Conclusion
We have demonstrated that the patient-specific prostate VMAT QA results may be directly estimated from gantry angle errors or gantry accelerations by analyzing the log files, thereby providing potential to simplify patient-specific prostate VMAT QA pro- cedure by improving efficiency and laborsaving. Evaluation for other tumor sites is needed for further comprehensive insights.
Acknowledgements
The authors thank all the radiological technologists from the Department of Radiological Technology, Hyogo College of Medicine College Hospital (Nishinomiya, Hyogo, Japan) for their general guidance and encouragement for this work, and they also acknowledge Kiyoshi Yoda from Elekta KK for his invaluable comments on this research.