1. Introduction
The soybean aphid, Aphis glycines (Hemiptera: Aphididae), is an invasive herbivore new to North America. It was first discovered in North America in Wisconsin in late July 2000 infesting soybean crop. High soybean aphids densities damage soybean plants
by reducing plant height, pod number and total yields, and yield reductions measured from grower strip trials have ranged from 12 to 45% [1] . The soybean aphid is a small sap-succking and partenogenetically reproducing insect. Females are produced during spring and summer. During the summer or early fall, the population will produce winged males along special winged females called gynoparae. These aphids move to their overwintering host, buckthorn, Rhamnus sp., where mating occurs and at least one generation occurs. It is one of the major insect pests of soybean reproducing stages when high populations may build up and can cause great damage [2] . An economic threshold was developed for chemical control, i.e., when an insecticide treatment is warranted. According to [3] , the economic thresholds for the soybean aphids have been developed and vary from 250 to 273 aphids per plant. The control measures are not introduced before reaching the economic threshold. These thresholds are mainly for pesticide use, despite the fact that some naturally occurring predators such as the insidious flower bug, Orius insidiosus (Hemiptera: Anthocoridae), the most common and important predator ( [3] [4] ). Field studies have demonstrated that the insidious flower bug can significantly slow soybean aphid population growth, particularly during hot summer weather ( [5] [6] ). Soybean aphid populations can grow to extremely high levels under favorable environmental conditions. Reproduction and development is faster when temperatures are between 25˚C and the mid 29˚C when population can double in two or three days. The aphids are greatly affected by temperatures above 30˚C, and they are reported to begin to die when temperatures reach 35˚C [1] . We proposed in [7] a fuzzy chemical control to soybean aphid, that is, the model provides how often and how much to apply the insecticides on the plants. This work describes a method based in Mamdani Fuzzy Control [8] to build a model to evaluate the interaction of the prey, A. glycines (the soybean aphid) and the predator, O. insidiosus (Hemiptera: Anthocoridae), considering the effects of the temperature in the growth of the prey population [1] . Subsequently, we propose a biological control to soybean aphid by another fuzzy rule-based system. The dynamic model results in a fuzzy model that preserves the biological meaning and nature of the predator-prey model, that is, the fluctuations in the population density of both species and the peaks in the density of the prey and predator alternate. The aim of this investigation is to propose a specific method to enhance current decision making tools to control this pest. On the one hand, the soybean aphid is still a quarantine pest in Brazil. Therefore, before any eventual invasion, a predictive model to enhance biological control program is desirable, because the predator is present in Brazil. On the other hand, the soybean aphid has become the most devastating insect pest of soybeans in the United States. Brazil is the second largest exporter of soybean at present, after the USA and before Argentina. According to the Bureau of Agriculture of the USA, it has been estimated that Brazil will be the largest soybean exporter in 2023. Therefore, considering the economic importance of soybeans in Brazil, we need to be prepared for effective proposals to control soybean aphids or any other invasive pest.
2. Preliminaries
2.1. Predation
Predation is an example of the interaction between two populations that results in negative effects on growth and survival of one population (prey) and in positive or beneficial effects to the other (predator). A predator is an organism that hunts and kills other organisms for food [9] . Prey populations grow when predators are absent. Predators depend on the presence of their prey to survive. An encounter is assumed to decrease the prey population and increase the predator population by contributing to their growth. We present hypotheses that characterize a predator-prey model, that is:
・ If the number of predators is small, the number of prey increases;
・ If the number of predators is large, the number of prey decreases;
・ If the number of prey is large, the number of predators increases;
・ If the number of prey is small, the number of predators decreases.
According to these hypotheses [10] , we have established fuzzy rule base instead of usual differential equations that characterize the classic deterministic models. This rule base replaces differential equations, which characterize the classic deterministic models used to model the dynamics between prey and predators. These hypotheses are qualitative information that allow us to propose rules that relate (at least partially), the numbers in the populations with their own variations ( [11] [12] ). In fact, our main interest in this paper is to elaborate a predator-prey model that represents the interaction between soybean aphids (prey) and their predators using fuzzy rule-based systems, because some parameters of the differential equations are not available yet in the literature.
2.2. Fuzzy Rule-Based System
Next we develop brief reviews of the concept of fuzzy set and fuzzy rule-based system, and we detail the fuzzy model suggested in this paper. Fuzzy Sets and Fuzzy Logic have become one of the emerging areas in contemporary technologies of information processing. Fuzzy Sets Theory was first developed by Zadeh [13] in the mid-1960s to represent uncertain and imprecise knowledge. It provides an approximate but effective means of describing the behavior of the system that is too complex, ill defined, or not easily analyzed mathematically, and this is our case. A fuzzy set A is characterized by a membership function, A, mapping the elements of a domain X to the unit interval [0,1]. That is,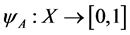 . Clearly, a fuzzy set is a generation of the concept of a set whose membership function takes on only two values {0,1}, that is, the characteristic function of A,
. Clearly, a fuzzy set is a generation of the concept of a set whose membership function takes on only two values {0,1}, that is, the characteristic function of A,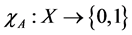 . Fuzzy variables are processed using a fuzzy rule-based system. A general fuzzy rule-based system consists of four components: an input processor (fuzzification), a fuzzy rule base; a fuzzy inference method and an output processor (defuzzification). These components process real-valued inputs in order to provide real-valued outputs (see Figure 1).
. Fuzzy variables are processed using a fuzzy rule-based system. A general fuzzy rule-based system consists of four components: an input processor (fuzzification), a fuzzy rule base; a fuzzy inference method and an output processor (defuzzification). These components process real-valued inputs in order to provide real-valued outputs (see Figure 1).
The fuzzification is the process in which the input values of the system are converted into appropriate fuzzy sets of their respective universes. It is a mapping of the domi-
![]()
Figure 1. Structure of fuzzy rule-based systems.
nion of the real numbers led to the fuzzy dominion [14] . Expert knowledge plays an important role to build the membership functions for each fuzzy set associated with the inputs. The rule base characterizes the objectives and strategies used by specialists in the area through of a linguistic rule set. It is composed by a collection of fuzzy conditional propositions in the form if-then rules [14] . The fuzzy inference method performs an approximate reasoning using the compositional rule of inference. A particular form of fuzzy inference of interest here is the Mamdani inference method [15] . In this case, it aggregates the rules through the logical operator OR, modeled by the maximum operator and, in each rule, the logical operators AND and THEN are modeled by the minimum operator [15] . The logic of decision to be made, incorporated to the structure of inference of the rule base, uses fuzzy implications to simulate the decisions that are wanted [14] . It generates actions inferred from consequents a set of input conditions - antecedents (see Figure 2).
Finally, in defuzzification, the value of the output linguistic variable inferred from the fuzzy rule is translated to a real value. The output processor task is to provide real- valued outputs using defuzzification, which is a process that chooses a real number that is representative of the inferred fuzzy set. A typical defuzzification scheme adopted in this paper is the centroid or center of mass method [15] . According to [14] fuzzy set approaches have been developed for special purposes where the information basis has been vague and imprecise. Under these conditions fuzzy techniques allow more accurate conclusions in comparison to the other approaches which cannot be applied successfully because of lack of data.
3. The Mathematical Model for the Interaction between Soybean Aphids and Their Predator
This work describes a method based in Mamdani fuzzy control [8] to elaborate a model that studies the interaction of the prey, A. glycines (soybean aphids), and the predator, O. insidiosus [5] , and the effects of the temperature in the growth of the prey population [1] . Our fuzzy mathematical model is composed of a predator-prey fuzzy system considering the temperature data.
The variables of the fuzzy system are number of prey -x-, number of the predators -y- (input variables) and their variations (output variables). The fuzzy sets of the input variables, defined by experts, are {small, small medium, large medium, large} (that is, the triangular functions defined in the interval [0,1000] for the number of prey and in the interval [0,0.3] for the number of predators) and the fuzzy sets of the output variables are {small positive, large positive, small negative, large negative} (that is, the triangular functions defined in the interval [−0.4,0.4] for the variation of the prey - - and in the interval [−0.1,0.2] for the variation of the predators―
- and in the interval [−0.1,0.2] for the variation of the predators― ) [6] (see Figure 3).
) [6] (see Figure 3).
Considering the hypotheses of the predation and qualitative information from expertise, in particular by an entomologist, allow us to propose rules that relate to the variables of state, with their own variations. We have elaborated 16 rules of the system (S1):
・ If (x is small) and (y is small) then ( is large-positive) and (
is large-positive) and (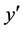 is large-negative);
is large-negative);
・ If (x is small-medium) and (y is small) then (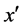 is large-positive) and (
is large-positive) and (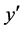 is small- negative);
is small- negative);
・ If (x is large-medium) and (y is small) then (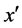 is large-positive) and (
is large-positive) and (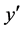 is small- positive);
is small- positive);
・ If (x is large) and (y is small) then (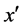 is large-positive) and (
is large-positive) and (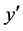 is large-positive);
is large-positive);
・ If (x is small) and (y is small-medium) then ( is small-positive) and (
is small-positive) and ( is large- negative);
is large- negative);
・ If (x is small-medium) and (y is small-medium) then (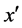 is small-positive) and (
is small-positive) and (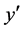 is small-negative);
is small-negative);
・ If (x is large-medium) and (y is small-medium) then (![]() is small-positive) and (
is small-positive) and (![]() is small-positive);
is small-positive);
・ If (x is large) and (y is small-medium) then (![]() is small-positive) and (
is small-positive) and (![]() is large- positive);
is large- positive);
・ If (x is small) and (y is large-medium) then (![]() is small-negative) and (
is small-negative) and (![]() is large- negative);
is large- negative);
・ If (x is small-medium) and (y is large-medium) then (![]() is small-negative) and (
is small-negative) and (![]() is small-negative);
is small-negative);
・ If (x is large-medium) and (y is large-medium) then (![]() is small-negative) and (
is small-negative) and (![]() is small-positive);
is small-positive);
・ If (x is large) and (y is large-medium) then (![]() is small-negative) and (
is small-negative) and (![]() is large- positive);
is large- positive);
・ If (x is small) and (y is large) then (![]() is large-negative) and (
is large-negative) and (![]() is large-negative);
is large-negative);
・ If (x is small-medium) and (y is large) then (![]() is large-negative) and (
is large-negative) and (![]() is small- negative);
is small- negative);
・ If (x is large-medium) and (y is large) then (![]() is large-negative) and (
is large-negative) and (![]() is small- positive);
is small- positive);
・ If (x is large) and (y is large) then (![]() is large-negative) and (
is large-negative) and (![]() is large-positive).
is large-positive).
Hence, we have obtained the variation rates of the populations from Mamdani Inference method and the fuzzification of the center-of-gravity. Regarding the influence of the temperature abiotic factor in the population of soybean aphids, [1] got the intrinsic rate of increase (see Table 1).
Using an adjustment from least-squares method, we have estimated an intrinsic rate of increase:
![]() (1)
(1)
![]()
Table 1. Data of soybean aphids at four constant temperatures on soybean. Source: [1] .
where T is the temperature (see Figure 4).
In the numerical simulations performed, we have observed the variation of the number of the prey and the number of the predators considering the temperature. In order to achieve this, we have considered an initial number of aphids, ![]() , an initial number of predators,
, an initial number of predators, ![]() , in a plant and the temperature,
, in a plant and the temperature, ![]() in the instant
in the instant![]() . From Equation (1) we have obtained
. From Equation (1) we have obtained ![]() (variation of
(variation of ![]() due the temperature
due the temperature![]() ). The fuzzy predator-prey system (S1) produces
). The fuzzy predator-prey system (S1) produces ![]() and
and ![]() as output values from the initial conditions and
as output values from the initial conditions and ![]() by Equation (1) in order to get
by Equation (1) in order to get ![]() and
and![]() . Thereby, in each iteration, we have the following:
. Thereby, in each iteration, we have the following:
![]() (2)
(2)
that is, Euler’s Method, where h is the increment.
Numerical Simulations
We have obtained the variation of the number of the prey and the number of the predators in the numerical simulation. Let ![]() be an initial number of aphids and
be an initial number of aphids and ![]() be an initial number of predators per plant (input variables of the system (S1) and the time-at-temperature derived from Figure 5.
be an initial number of predators per plant (input variables of the system (S1) and the time-at-temperature derived from Figure 5.
Simulations of the trajectories produced by the fuzzy model follow the steps below:
1) Given an initial number of the prey population (![]() ) and an initial number of the predator population (
) and an initial number of the predator population (![]() ) as input data of the one fuzzy rule-based system (S1);
) as input data of the one fuzzy rule-based system (S1);
2) The fuzzy rule-based system of the predator-prey type gives the output data: ![]() and
and![]() ;
;
3) Given an initial temperature T (mean temperature in Figure 5), by Equation (1) we estimate![]() ;
;
4) From Equations (2), we find ![]() and
and![]() ;
;
5) ![]() and
and ![]() are the input data of the fuzzy rule-based system of the predator-prey type (S1) and so forth (see Figure 6).
are the input data of the fuzzy rule-based system of the predator-prey type (S1) and so forth (see Figure 6).
We used the data available in [16] , i.e., 2004 and 2005, because there are not more current data available that used the same research methodology.
The phase plane by this fuzzy system (dashed line) and the phase plane by the real data (black points) [16] are illustrated in Figure 7.
Now, we have a set of real data and another of simulated ones (Figure 7).
Deviance measures are applicable when real and simulated data can be paired at the same time. These are based on the differences between the simulated and real
![]()
Figure 4. Temperature (T) × intrinsic rate of increase of soybean aphids (![]() ).
).
![]() (a)
(a)![]() (b)
(b)
Figure 5. Climatic parameters (temperature and rain) registered during the soybean aphid infestation periods in 2004 (a) and 2005 (b). Data obtained from weather station at Haskell Agricultural Laboratory (Northeast Research and Extension Center), Concord, NE, USA.
![]()
Figure 6. Structure of the mathematical model to obtain the populations ![]() and
and![]() .
.
values. According to [17] for numerical data, a commonly used measure is a mean relative error (MRE) defined as
![]() (3)
(3)
where![]() represents the observed values,
represents the observed values, ![]() the simulated values by the model and n the number of data.
the simulated values by the model and n the number of data.
The value MRE for 2004 data (Figure 7) is 0.1376, which indicates a concordance of 86.24% between the results obtained from our model and real data. And, the values MRE for 2005 data (Figure 7) is 0.1870, which indicates a concordance of 81.30% between the results obtained from our model and real data.
In next section we use this mathematical model to predict the timing and the number of predators released for soybean aphid control.
4. Fuzzy Biological Control
Biological control is the use of natural enemies to control insect pests. It is defined as the regulation by natural enemies of the population density of another organism at a lower average than would otherwise occur ( [4] [18] ).
The control of pests below the level at which they cause economic thresholds by the deliberate introduction of exotic natural enemies is referred to as classical biological control [18] .
In this way, we have proposed biological control via fuzzy system, since there is no model available for biological control of soybean aphids.
A method to determine if an insecticide treatment is warranted is a conventional method using the 250 aphids per plant economic as the threshold with 80% of the plants infested and aphids population increasing [3] .
Considering the above-mentioned hypotheses, we have observed the variation of the number of prey and the number of predators in the numerical simulation. Let ![]() be an initial number of soybean aphids (input variable of the fuzzy system) and
be an initial number of soybean aphids (input variable of the fuzzy system) and ![]() be an initial number of predators per plant by fuzzy predator-prey system (S1). Considering the above-mentioned hypotheses, we have calculated the introduction of the quantity of the predator―the variable
be an initial number of predators per plant by fuzzy predator-prey system (S1). Considering the above-mentioned hypotheses, we have calculated the introduction of the quantity of the predator―the variable![]() ―depending on the quantity of the soybean aphids―the variable x―and of the insidious flower bugs―the variable y―presents in the plants by fuzzy rule-based system. Hence, the variables of this system are the number of prey and the number of predators (input variables) and the quantity of the predators that will be released (output variable) per plant in the plantation. The fuzzy sets of the input variables are still the same of fuzzy predator-prey system (S1). The fuzzy sets of output variable are the same of the input variable y of fuzzy predator-prey system (S1) added to the fuzzy set null (that is, (null, small, small medium, large medium, large), where null is the triangular function (0,0,0)).
―depending on the quantity of the soybean aphids―the variable x―and of the insidious flower bugs―the variable y―presents in the plants by fuzzy rule-based system. Hence, the variables of this system are the number of prey and the number of predators (input variables) and the quantity of the predators that will be released (output variable) per plant in the plantation. The fuzzy sets of the input variables are still the same of fuzzy predator-prey system (S1). The fuzzy sets of output variable are the same of the input variable y of fuzzy predator-prey system (S1) added to the fuzzy set null (that is, (null, small, small medium, large medium, large), where null is the triangular function (0,0,0)).
In this way, we propose the following rule base of the fuzzy biological control system (S2):
1) If (x is small) and (y is small) then (![]() is null);
is null);
2) If (x is small-medium) and (y is small) then (![]() is large-medium);
is large-medium);
3) If (x is large-medium) and (y is small) then (![]() is large);
is large);
4) If (x is large) and (y is small) then (![]() is large);
is large);
5) If (x is small) and (y is small-medium) then (![]() is null);
is null);
6) If (x is small-medium) and (y is small-medium) then (![]() is large-medium);
is large-medium);
7) If (x is large-medium) and (y is small-medium) then (![]() is large);
is large);
8) If (x is large) and (y is small-medium) then (![]() is large);
is large);
9) If (x is small) and (y is large-medium) then (![]() is null);
is null);
10) If (x is small-medium) and (y is large-medium) then (![]() is small);
is small);
11) If (x is large-medium) and (y is large-medium) then (![]() is large-medium);
is large-medium);
12) If (x is large) and (y is large-medium) then (![]() is large);
is large);
13) If (x is small) and (y is large) then (![]() is null);
is null);
14) If (x is small-medium) and (y is large) then (![]() is small);
is small);
15) If (x is large-medium) and (y is large) then (![]() is small-medium);
is small-medium);
16) If (x is large) and (y is large) then (![]() is large-medium).
is large-medium).
We obtain the quantity released of the predators from Mamdani inference method and the fuzzification of the center-of-gravity represented in Figure 8.
Figure 8 illustrates the quantity of the predators that will be released per plant that might be applied depending on the number of soybean aphids and the insidious flower bugs, i.e., from the population density of prey and of predators, we obtain the quantity of the predators to be included in the plantation by fuzzy control (S2). We suggest using this as a policy of the biological control of soybean aphids, because the fuzzy system provides how often and how much to include the quantity of predators per plant.
Numerical Simulations
From ![]() and
and ![]() by Equations (2), we obtain the quantity of the predators that will be released,
by Equations (2), we obtain the quantity of the predators that will be released, ![]() , by fuzzy system (S2), that is:
, by fuzzy system (S2), that is:
![]() (2)
(2)
in Figure 9.
The evolution of the population is contingent on the prey and predators over time given by the fuzzy model are depicted in Figure 10 and Figure 11 with addition of the predators, when the population of prey exceeds 250 per plant.
Now, it is necessary to determine the day that needs to be done the deliberate introduction of predators, according to the number of iteration in the computer simulations.
Linear regression analysis using the least-squares method was used to estimate the days aforementioned are given by the equation:
![]() (4)
(4)
where t is the number of iterations in the computer simulations.
![]()
Figure 8. The solution of the fuzzy system (S2):![]() .
.
![]()
Figure 9. Structure of the fuzzy biological control.
![]()
Figure 10. The evolution of the population over time with ![]() (initial number of aphids),
(initial number of aphids), ![]() (initial number of predators) and the temperature from Figure 2 for 2004 without and with addition of the predators in plantation.
(initial number of predators) and the temperature from Figure 2 for 2004 without and with addition of the predators in plantation.
In the case of Figure 10, it should be included 0.1628 predators per plant in the 26th day (Equation (4)) because the population of prey exceeded 250 per plant (threshold) in the 26th day.
In the case of Figure 11, it should be included 0.1575 predators per plant in the 46th day, because the population of prey exceeded 250 per plant (threshold) in the 46th day, demonstrating the importance of the biological control via predation and a constant monitoring of the plantation since the arrival of soybean aphids.
5. Discussion
We propose the fuzzy model to simulate soybean aphid population dynamics that in-
![]()
Figure 11. The evolution of the population over time with ![]() (initial number of aphids),
(initial number of aphids), ![]() (initial number of predators) and the temperature from Figure 2 for 2004 without and with addition of the predators in plantation.
(initial number of predators) and the temperature from Figure 2 for 2004 without and with addition of the predators in plantation.
cludes biotic (predator) and abiotic (temperature) factors. This model is based on fuzzy system (S1) that relates the input variables (number of prey, number of predators) with the output variables (variation of prey and variation of predators) and Equation (1). The use of a fuzzy rule-based system instead of usual differential equations characterizes the classic deterministic models, because many parameters of the differential equations are not available. In addition, the qualitative information and data reported in the literature [16] could contribute to the appropriate elaboration of the rule base and the fuzzy sets.
Results demonstrate that the fuzzy mathematical model provides the phase plane that preserves the characteristics of the phase plane of a predator-prey model, that is, dynamic model results in a fuzzy model that preserves the biological meaning and nature of the predator-prey model.
As demonstrated by the above simulations, we can see that the temperature influences the growth of the aphids population [1] and a comparison between the fuzzy model and real data [16] .
Next, we use this mathematical model to predict the timing and the number of predators released for soybean aphid biological control.
The concern about the environment has been increasingly important. Currently, actions aimed at sustainable management of natural resources are goals.
In general, pesticides are toxic, harmful to human health and the environment. One of the most common problems is the contamination of soil, groundwater, rivers and lakes. When the pesticide is used, it intoxicates all life present. Studies show the decrease in the number of pollinating bees and the destruction of bird habitat in environments where pesticides are used [19] .
The abusive use of insecticides may lead to an increase number of pests because pests become more resistant, requiring stronger pesticides that will damage the environment even more and will kill the pests’ natural predators [19] .
There is some evidence that biological control can be favorable where a pest is causing damage in a plantation [18] .
Considering that the time between the appearance of aphids on the plant and the maturation stage of grains is 60 days on average, the Figures 10 and 11 demonstrated the importance of the biological control via predation and a constant monitoring of the plantation from the initial arrival of soybean aphids. In addition, the most likely alternative, chemical control is undoubtedly damaging to the environment ( [4] [18] [19] ).
Thus, in this paper we have proposed a biological control based on the introduction of predators in the plantation when the prey population exceeds the economic damage threshold.
6. Conclusions
This study has suggested that the use of the Mamdani Control Fuzzy in Ecology may represent the interaction among species in the environment where the available data are few or qualitative. We have used intuitive hypotheses of the dynamics of aphids- insidious flower bug and data reported in the literature to elaborate the model without explicit differential equations. It was clear that temperature was an important factor on the growth of aphids population. We would like to highlight the advantages of using fuzzy rule-based models compared to the deterministic models (differential equations, for example):
・ The input and output sets of fuzzy rule-based systems may be easily defined by experts, that is, specialists who may know when the population of a particular species is small, large and so forth of the predators population over time.
・ We have used a rule base instead of systems given by equations and this avoids the difficulty of obtaining the parameters.
・ If it is necessary to know the parameters, they may be obtained through a curve fitting of the solution generated by the fuzzy model. That is, the parameters may be obtained through a curve fitting procedure from the solution obtained from the fuzzy rule-based model.
・ We suggest using this as a policy to biological control of soybean aphids because the fuzzy biological control model provides how often and how much to add the predators in the plantation, instead using insecticides, in a simple, intuitive and a direct way.
・ We will develop further studies on simple and specific method using a fuzzy rule- based system to help the implementation of an integrated pest management system of this one.
Acknowledgements
The first author acknowledges the Coordination for the Improvement of Higher Education Personnel (CAPES) and the second author acknowledges the National Council for Scientific and Technological Development (CNPq), project numbers 305862/2013- 8, for the financial support.