Sample Size Calculation of Exact Tests for the Weak Causal Null Hypothesis in Randomized Trials with a Binary Outcome ()
1. Introduction
In superiority randomized trials in which subjects are assigned to one of two treatment groups and the outcome is binary, data can be summarized in a two-by-two contingency table. Investigators are often interested in testing the equality of the causal risks of the two groups, using a hypothesis test. A popular method for the hypothesis test is Fisher’s exact test [1] [2] . However, the null hypothesis of this test is that the causal effect of treatment is the same for all subjects. This null hypothesis is referred to as the sharp causal null hypothesis [3] - [5] ; rejection of this null hypothesis does not mean that the causal risks of the two groups are different, i.e., the causal risk difference is not zero. Therefore, it is inevitable to examine the null hypothesis that the causal risks are equal in the two groups, which is referred to as the weak causal null hypothesis [3] - [5] , to make an inference about the average causal effect of treatment. Nevertheless, few hypothesis tests for the weak causal null hypothesis have been discussed.
Recently, two exact tests for the weak causal null hypothesis were developed [6] ; one is a conditional exact test, which requires that a marginal total is fixed, and the other is an unconditional exact test, which does not require that a marginal total is fixed and depends rather on the ratio of random assignment. Under simple (or equally complete) randomization, the unconditional exact test, rather than the conditional exact test, may be applied, because the number of subjects assigned to each group is not fixed under simple randomization. Conversely, under randomization with any restriction, the conditional exact test, rather than the unconditional exact test, may be applied. These exact tests have the advantages that they are not based on large sample theories and do not require any assumptions, and they can be extended to non-inferiority trials and to the construction of a confidence interval (CI) in a straightforward manner. Therefore, these exact tests can be applied as a unified approach.
To conduct statistical hypothesis testing in an actual randomized trial, the sample size need in the trial must be calculated during the study design. Moher et al. [7] wrote the following about the necessity of sample size calculation as follows: “For scientific and ethical reasons, the sample size for a trial needs to be planned carefully, with a balance between medical and statistical considerations. Ideally, a study should be large enough to have a high probability (power) of detecting as statistically significant a clinically important difference of a given size if such a difference exists.” A randomized trial with a smaller sample size than the sample size needed may cause type I or II error and produce a scientifically unreliable result. Conversely, an excessive sample size may cause ethical problems, because researchers have to evaluate more subjects. Although some sample size calculation methods have been developed [8] [9] and compared [10] - [12] , none have been applied to the weak causal null hypothesis. Therefore, in this paper, we present a procedure for calculating the sample size for the conditional and unconditional exact tests introduced by Chiba [6] .
The paper is organized as follows. In Section 2, we describe the notation used throughout this paper. In Section 3, we review the unconditional and conditional exact tests. In Section 4, we present a procedure of the sample size calculation for these exact tests. The procedure is examined through a numerical example in Section 5. Finally, we discuss the results in Section 6 and state the conclusion in Section 7.
2. Notation
Throughout this paper, we denote X as the assigned treatment; X = 1 if a subject was assigned to the treatment group, and X = 0 if assigned to the control group. Y denotes the binary outcome; Y = 1 if the event occurred, and Y = 0 if it did not. The results are summarized in Table 1, where a, b, c, d, and n are the numbers of subjects.
For each subject, it is also possible to consider the potential outcomes [13] [14] that correspond to the subject’s outcome had he/she been in the other trial group. Yi(x) denotes the potential outcome for ith subject i (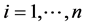 ) under X = x. Using the potential outcomes, we consider the following four types of subject to define the four principal strata:
) under X = x. Using the potential outcomes, we consider the following four types of subject to define the four principal strata:
i) Type 11: individuals who would experience the event regardless of the assigned treatment group; i.e., (Yi(1), Yi(0)) = (1, 1).
ii) Type 10: individuals who would experience the event if assigned to the treatment group but would not experience the event if assigned to the control group; i.e., (Yi(1), Yi(0)) = (1, 0).
iii) Type 01: individuals who would not experience the event if assigned to the treatment group but would experience the event if assigned to the control group; i.e., (Yi(1), Yi(0)) = (0, 1).
iv) Type 00: Individuals who would not experience the event regardless of the assigned treatment group; i.e., (Yi(1), Yi(0)) = (0, 0).
Note that all subjects belong to one of these four types.
Let nst denote the number of subjects with (Yi(1), Yi(0)) = (s, t), where s, t = 0, 1. The causal risk if all subjects were assigned to the treatment group (X = 1) can be expressed as
 (1)
(1)
This is because only subjects with type 11 or type 10 would experience the event. Likewise, the causal risk if all subjects were assigned to the control group (X = 0) can be expressed as
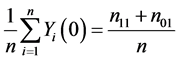 , (2)
, (2)
because only subjects with type 11 or type 01 would experience the event. Therefore, the sample average treatment effect (the difference between (1) and (2)) can be expressed
![]()
Table 1. Two-by-two contingency table obtained from a randomized trial, where a, b, c, d, and n indicate the number of subjects.
as
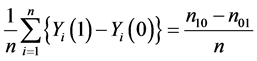 , (3)
, (3)
and thus the null hypothesis can be expressed as
H0: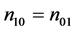 , (4)
, (4)
which corresponds to the weak causal null hypothesis of
H0: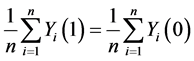 . (5)
. (5)
This null hypothesis will be the main interest in many clinical trials.
Here, we consider the null hypothesis of
H0: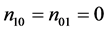 , (6)
, (6)
which is a special case for the weak causal null hypothesis (4). The null hypothesis (6) implies that the combination of (Yi(1), Yi(0)) is limited to (Yi(1), Yi(0)) = (1, 1) or (0, 0), and thus subjects with (Yi(1), Yi(0)) = (1, 0) or (0, 1) do not exist. Therefore, this null hypothesis corresponds to the following sharp causal null hypothesis:
H0:  for all subjects, (7)
for all subjects, (7)
which is also a special case for the weak causal null hypothesis (5). It is obvious that the weak causal null hypothesis holds whenever the sharp causal null hypothesis holds. However, in general, the rejection of the sharp causal null hypothesis does not mean that the weak causal null hypothesis is rejected (i.e., ) [6] .
) [6] .
3. Exact Tests for the Weak Causal Null Hypothesis
3.1. Unconditional and Conditional Exact Tests
When the random assignment is conducted by the ratio of 1:r, we assume that subjects are assigned as in Table 2 under the weak causal null hypothesis; i.e., of the nst subjects, nst,1 subjects are assigned to the treatment group (X = 1) with the probability of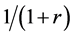 , and nst,0 subjects are assigned to the control group (X = 0) with the probability of
, and nst,0 subjects are assigned to the control group (X = 0) with the probability of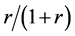 . Then, as each subject is independently assigned, the probability that nst,1 of nst subjects are assigned to the treatment group can be expressed as follows:
. Then, as each subject is independently assigned, the probability that nst,1 of nst subjects are assigned to the treatment group can be expressed as follows:
 , (8)
, (8)
where , and the following set of conditions is required:
, and the following set of conditions is required:
Set of conditions 1:
 ,
,  ,
, 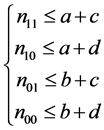 and
and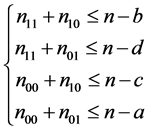 . (9)
. (9)
![]()
Table 2. Two-by-two contingency table with the numbers for the four types of subjects defining the four principal strata.
The first condition is the null hypothesis (4), and the second is the total number of subjects. The last two conditions are derived on the basis of Table 1 and Table 2; e.g., ![]() is derived from
is derived from![]() , and
, and ![]() is derived from
is derived from![]() .
.
The risk difference estimated from the observed data, RDO, is
![]() (10)
(10)
from Table 1, and the risk difference under the null hypothesis, RDN, is
![]() (11)
(11)
from Table 2. In this paper, we consider only the case of RDO ≤ 0, but the following methods can easily be applied to the case of RDO ≥ 0. For RDO ≤ 0, the unconditional exact test yields the one-sided p-value, p, using the following formula:
![]() (12)
(12)
with
![]() , (13)
, (13)
where I(z) = 1 if z ≤ 0 and I(z) = 0 if z > 0 with z = RDN − RDO (the difference between (11) and (10)). This is the unconditional exact test introduced by Chiba [6] .
For the conditional exact test, the numbers of subjects assigned to the two groups are fixed. Thus, instead of the probability (8), the following probability is used:
![]() , (14)
, (14)
where the following conditions are required:
Set of conditions 2: Set of conditions 1 (9) plus![]() . (15)
. (15)
Consequently, the conditional exact test yields the one-sided p-value, p, using the following formula:
![]() (16)
(16)
with
![]() . (17)
. (17)
We note that, under the following monotonicity assumption [15] [16] :
Assumption 1 (monotonicity): ![]() for all subjects, (18)
for all subjects, (18)
the weak causal null hypothesis (4) is equivalent to the sharp causal null hypothesis (6). This is because there is no subject with type 10, i.e., n10 = 0, under this assumption. We further note that the conditional exact test degenerates to Fisher’s exact test under the monotonicity assumption (18) [6] .
In this paper, we define a two-sided p-value as twice the one-sided p-value.
3.2. Extension to Non-Inferiority Trials
Hypothesis tests of non-inferiority focus on the null hypothesis of H0: ![]() rather than H0:
rather than H0:![]() , where δ (> 0) is a small quantity specified in advance. Therefore, from the formula (3), the null hypothesis for non-inferiority can be expressed as n10 − n01 = δn. To take the case in which δn is not an integer value into account, we set the null hypothesis to a maximum integer value satisfying n10 − n01 ≤ δn. Consequently, for non-inferiority trials, the one-sided p-value can be calculated by substituting n10 = n01 in the set of conditions 1 (9) by n10 − n01 = m, where m is a maximum integer value satisfying m ≤ δn.
, where δ (> 0) is a small quantity specified in advance. Therefore, from the formula (3), the null hypothesis for non-inferiority can be expressed as n10 − n01 = δn. To take the case in which δn is not an integer value into account, we set the null hypothesis to a maximum integer value satisfying n10 − n01 ≤ δn. Consequently, for non-inferiority trials, the one-sided p-value can be calculated by substituting n10 = n01 in the set of conditions 1 (9) by n10 − n01 = m, where m is a maximum integer value satisfying m ≤ δn.
We note that we can also yield the 100α (%) CI, which is a CI corresponding to a significance level of α (two-sided), by finding the range in which the null value of n10 − n01 is not rejected at a significance level of α/2 based on the two separate one-sided hypothesis tests. Chiba [17] demonstrated that such an exact CI was narrower than that using the other approaches [18] [19] to derive as an exact CI for a data set.
4. Sample Size Calculation
In the situation in which a randomized clinical trial with the assignment ratio 1:r is planned, we set the sample size in the treatment group to ![]() and that in the control group to
and that in the control group to![]() , where the total number is N = N1 + N0. Furthermore, we set the response probabilities under the alternative hypothesis as follows: P1 if all subjects are assigned to the treatment group, and P0 if all subjects are assigned to the control group.
, where the total number is N = N1 + N0. Furthermore, we set the response probabilities under the alternative hypothesis as follows: P1 if all subjects are assigned to the treatment group, and P0 if all subjects are assigned to the control group.
First, we derive the power function for a given sample size N for the unconditional exact test. When the one-sided p-value is set to α/2, the power function can be derived by the following procedure:
1) Derive combinations of (n11, n10, n01, n00) under the alternative hypothesis, which satisfy n10 − n01 = MA, where MA is a maximum integer value satisfying ![]() ,
, ![]() , and
, and![]() .
.
2) For each combination of (n11, n10, n01, n00) in Step 1, derive all combinations of (a, b, c, d), which can be obtained as observed data under the combination of (n11, n10, n01, n00), from a = n11,1 + n10,1, b = n01,1 + n00,1, c = n11,0 + n01,0, d = n10,0 + n00,0 (see Table 1 and Table 2), and calculate the probability (8).
3) For each combination of (n11, n10, n01, n00), (a, b, c, d) and the probability (8) in Step 2, using the other combination ![]() corresponding to (a, b, c, d), derive the one-sided p-value from the unconditional exact test for the null hypothesis of H0:
corresponding to (a, b, c, d), derive the one-sided p-value from the unconditional exact test for the null hypothesis of H0:![]() , where MN is a maximum integer value satisfying MN ≤ δN (δ = 0 for the superiority trial and δ > 0 for the non-inferiority trial).
, where MN is a maximum integer value satisfying MN ≤ δN (δ = 0 for the superiority trial and δ > 0 for the non-inferiority trial).
4) Derive the conditional power given (n11, n10, n01, n00), p*, by summing the probability (8) in Step 2 for cases in which the one-sided p-value in Step 3 is smaller than α/2.
5) Derive the power from inf{p*: (n11, n10, n01, n00)}.
In Step 5, we take the infimum. This is because we cannot know which combination of (n11, n10, n01, n00) is the most plausible from the assumed true values of P1 and P0. Nevertheless, if investigators have plausible information about (n11, n10, n01, n00), such as the monotonicity assumption (18), the power can be calculated using the information. The hypothesis test can also be performed using the information. The required sample size can be determined by the smallest integer value of N, such that the power derived in Step 5 is larger than or equal to the power given in advance.
For the conditional exact test, the power function is obtained by adding the condition of ![]() and applying the probability (14) instead of the probability (8) in Step 2 and by using the conditional exact test in Step 3.
and applying the probability (14) instead of the probability (8) in Step 2 and by using the conditional exact test in Step 3.
The procedure to calculate the power presented here examines all of the patterns that can be obtained as observed data under the alternative hypothesis by applying an exact test without large sample theories and any assumptions. Therefore, the calculated power is exact. However, the procedure requires large computer memory in addition to significant computing time, especially for the unconditional exact test. Unfortunately, it is very difficult to perform the procedure without any assumptions in actual clinical trials. In the next section, we will illustrate the procedure under the monotonicity assumption (18) using an example.
5. Numerical Example
For the illustration, we have used the data from a superiority randomized clinical trial to evaluate the effects of subcutaneous drainage during digestive surgery [20] . In this trial, patients who underwent an elective primary resection of colorectal cancer were randomized into either a group that would receive subcutaneous passive drainage (PD) or a group with no drainage (ND). The randomization was performed by the minimization method [21] , and the assignment ratio was 1:1. The endpoint was the incidence of superficial surgical site infections (SSI), and the result is summarized in Table 3. The risk difference is −0.066. Under the monotonicity assumption (18), the conditional exact test yields the one-sided p-value of 0.031 and 95% CI of (−32/246, 0/246) = (−0.130, 0.000). The unconditional exact test yields the one-sided p-value of 0.018 and 95% CI of (−33/246, −1/246) = (−0.134, −0.004).
For the sample size calculation, it was assumed that the true SSI incidence proportion would be 0.10 in the ND group and 0.02 in the PD group with a significance level of 0.05 (two-sided) and a power of 0.80 [20] . Under this setting and the monotonicity assumption (18), we examined the sample size calculation presented in Section 4 for both conditional and unconditional exact tests, and the arc sine approximation with continuity-correction [8] as a reference. These three power functions are displayed in Figure 1. The required sample size per group with a power ≥ 0.80 is 132 for the unconditional exact test, 144 for the conditional exact test, and 149 for the arc sine approximation with continuity-correction.
Figure 1 showed that the power for the unconditional exact test was the highest. The power for the conditional exact test was close to that for the arc sine approximation with continuity-correction for moderate to high powers, especially near a power of 0.80. Note that without the monotonicity assumption (18), the powers for the two exact tests would be lower than those in Figure 1. This is because we need to consider the other combinations of (n11, n10, n01, n00) with n10 ≠ 0, and these combinations may derive the lower power.
6. Discussion
In this paper, we proposed a sample size calculation method for the exact tests introduced by Chiba [6] , which are tests for the weak causal null hypothesis. The method can derive the exact power, because it examines all of the patterns that can be obtained as observed data under the alternative hypothesis by applying an exact test without large sample theories and any assumptions. However, unfortunately, it is very difficult
![]()
Table 3. Results from a superiority randomized clinical trial to evaluate the effects of subcutaneous drainage during digestive surgery.
![]()
Figure 1. Power functions under P1 = 0.02, P0 = 0.10, α/2 = 0.025, and δ = 0 for the assignment ratio of 1:1: the black solid line indicates the conditional exact test, the black broken line indicates the unconditional exact test, and the gray solid line indicates the arc sine approximation with continuity-correction.
to perform the presented methods in actual clinical trials without any assumptions such as the monotonicity assumption (18), due to limitations in computing power. Further work is needed to create an efficient algorithm and to develop an approximation method.
At present, for small to moderate sample sizes, randomization with any restriction is recommended rather than simple randomization to balance some background factors between two groups. This is natural if the same hypothesis testing method is applied under either randomization method. However, if a different hypothesis testing method corresponding to the randomization method is applied, the recommendation may be changed. In Section 5, the illustration showed that the power for the unconditional exact test was higher than that for the conditional exact test. This result could be predicted, because the p-value was smaller for the unconditional exact test compared with the conditional exact test. In general, the p-value will be smaller for the unconditional exact test than for the conditional exact test, because the conditional exact test is more discrete compared with the unconditional exact test by conditioning on![]() . In other words, in general, the power will be higher for the unconditional exact test compared with the conditional exact test. Consequently, if the unconditional exact test is applied under simple randomization and the conditional exact test is applied under randomization with any restriction, the test power will be higher under simple randomization than under randomization with any restriction. Although lack of balance of some background factors between the two groups is a problem for small to moderate sample sizes under simple randomization, this problem may be removed by stratified (adjusted) analysis, in which the covariates to be included in the analysis will be pre-specified in the protocol [22] . Such an analysis can increase the efficiency and power of a study without introducing a risk of bias [23] - [25] .
. In other words, in general, the power will be higher for the unconditional exact test compared with the conditional exact test. Consequently, if the unconditional exact test is applied under simple randomization and the conditional exact test is applied under randomization with any restriction, the test power will be higher under simple randomization than under randomization with any restriction. Although lack of balance of some background factors between the two groups is a problem for small to moderate sample sizes under simple randomization, this problem may be removed by stratified (adjusted) analysis, in which the covariates to be included in the analysis will be pre-specified in the protocol [22] . Such an analysis can increase the efficiency and power of a study without introducing a risk of bias [23] - [25] .
The unconditional exact test also has an advantage in that, for the sample size calculation, it takes into account cases in which the actual ratio of the numbers assigned to the two groups is not just 1:r, whereas the conditional exact test assumes that the ratio is just 1:r.
7. Conclusion
Whenever we conduct a statistical hypothesis test for the weak causal null hypothesis, which is the main interest in many clinical trials, we need to apply the corresponding sample size calculation method. Of the hypothesis tests, the unconditional test may have greater test power compared with the conditional test. The unconditional test and corresponding sample size calculation method should be discussed further.
Acknowledgements
The author thanks the reviewers for helpful comments. The author also thanks Dr. Masataka Taguri for introducing the paper [20] . This work was supported partially by Grant-in-Aid for Scientific Research (No. 15K00057) from Japan Society for the Promotion of Science.