A New Understanding of Equivalence of the Accelerating Field and the Gravitational Field ()

1. Preface
In recent decades, the study of relativity gradually is gradually becoming active. It is generally known that just like Newtonian Mechanics has its limitation, the relativity also has its limitation. So far, there is no experimental basis for the Relativistic space-time outlook, and the author’s study shows that problems exist in the Equivalence principle. When proving equivalence principle, Einstein just used several ideal experiments. The uniform acceleration elevator and the uniform rotating disc are the two most classic acceleration systems among the several ideal experiments. After careful analysis, the author discovered that the two most classic acceleration systems and the gravitational field are not completely equivalent.
2. The Uniform Acceleration Elevator and the Gravitational Field Is Not Completely Equivalent
2.1. Light Bending in Gravitational Field
According to the General Theory of Relativity, the light spreads out by a straight line in a vacuum without gravity, but it will bend in the gravitational field. Figure 1(a) is a schematic diagram of an elevator, let’s assume that the width of the elevator is 3 m. If the elevator is stationary in a vacuum without gravity, and the outside light gets in from the point 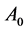 along the direction parallel to the floor of the elevator, it will reach the point
along the direction parallel to the floor of the elevator, it will reach the point 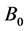 on the opposite wall of the elevator. In Figure 1(a), the author draws out a virtual line
on the opposite wall of the elevator. In Figure 1(a), the author draws out a virtual line , which indicates the linear propagation of the light in a vacuum. But if the elevator is stationary on the surface of a planet and the direction of gravity of the planet is shown in the arrow in the figure, the path of propagation of light in the gravitational field is curved. The outside light which gets in from the point
, which indicates the linear propagation of the light in a vacuum. But if the elevator is stationary on the surface of a planet and the direction of gravity of the planet is shown in the arrow in the figure, the path of propagation of light in the gravitational field is curved. The outside light which gets in from the point 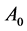 will reach the point
will reach the point  on the opposite wall of the elevator, the position of the point
on the opposite wall of the elevator, the position of the point 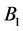 is a little lower than the point
is a little lower than the point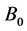 . In Figure 1(a), the author also draws out a curve
. In Figure 1(a), the author also draws out a curve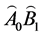 , which indicates that the light is bending in the gravitational field.
, which indicates that the light is bending in the gravitational field.
Theoretically, when the elevator is parked on the surface of the planet, the trajectory of the photon in the elevator should be a curve, but the width of the elevator is only 3 meters, in such a short distance when we calculate the deflection angle of the light, we can use a slash instead of a curve, and the result will remain unchanged. For this reason, in Figure 1(b), point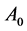 , point
, point 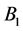 were connected by a solid line, the line
were connected by a solid line, the line 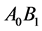 replaced the curve
replaced the curve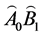 . The angle
. The angle  between solid line
between solid line 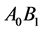 and dashed lines
and dashed lines 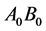 can be regarded as the deflection angle of light.
can be regarded as the deflection angle of light.
When the elevator is parked on the surface of the planet, we suppose that from point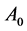 , the 1st light pulse gets in at time
, the 1st light pulse gets in at time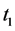 , the 2nd light pulse gets in at time
, the 2nd light pulse gets in at time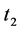 , …, the nth light pulse gets in at time
, …, the nth light pulse gets in at time![]() , the observer inside the elevator will find that the trajectories of the light pulses are consistent. That is to say, if every light pulse gets in form point
, the observer inside the elevator will find that the trajectories of the light pulses are consistent. That is to say, if every light pulse gets in form point![]() , they will get to the same point
, they will get to the same point ![]() on the opposite wall of the elevator. Their deflection angles of light are the same.
on the opposite wall of the elevator. Their deflection angles of light are the same.
Where the gravitational force is greater and the gravitational potential is deeper, the bending of the light is more powerful. The General Theory of Relativity predicts that the photon will be deflected at the edge of the sun, and deflection angle is:
![]()
Figure 1. (a) The bending light in the gravitational field; (b) the deflection angle of light in the gravitational field. gravitational field.
![]()
In the above formula, ![]() is the mass of the sun,
is the mass of the sun, ![]() is the radius of the sun. Experiments have already proved that the prediction given by the General Theory of Relativity is correct. Light will also deflect when passing through the earth’s surface. Use
is the radius of the sun. Experiments have already proved that the prediction given by the General Theory of Relativity is correct. Light will also deflect when passing through the earth’s surface. Use ![]() to represent the earth’s gravitational field, and use
to represent the earth’s gravitational field, and use ![]() to represent the gravitational field at the edge of the sun. Because the earth’s mass is far less than the sun’s mass, so
to represent the gravitational field at the edge of the sun. Because the earth’s mass is far less than the sun’s mass, so![]() , the deflection of the light is negligible and can be ignored in the earth’s reference frame.
, the deflection of the light is negligible and can be ignored in the earth’s reference frame.
2.2. Light Bending in Uniform Acceleration Elevator
Einstein believed that the gravitational field and the accelerating field are completely equivalent, so the light will also bend in the uniform acceleration rising elevator [1] . Figure 2 is also a schematic diagram of an elevator. The width ![]() of the elevator is also 3 m, and the light gets in from the point
of the elevator is also 3 m, and the light gets in from the point![]() . When the elevator is stationary, the light travels in straight lines reaching the point
. When the elevator is stationary, the light travels in straight lines reaching the point ![]() on the opposite wall of the elevator. In Figure 2, the author draws out a virtual line
on the opposite wall of the elevator. In Figure 2, the author draws out a virtual line ![]() to represent the rectilinear propagation of the light. The time the light requires from point
to represent the rectilinear propagation of the light. The time the light requires from point ![]() to get to point
to get to point ![]() is:
is:
![]() (1)
(1)
2.2.1. Estimation of Deflection Angle of Light in the Uniform Acceleration Elevator
The elevator in Figure 2 starts to do uniform acceleration movement at time![]() , with the accelerated speed a:
, with the accelerated speed a:
![]()
The direction of the arrow in the Figure 2 is the direction of the elevator acceleration. Suppose the initial velocity of the elevator is zero. In the gravitational field of the earth, the deflection effect of the light can be ignored, however, the following analysis shows that even in the case of![]() , the trajectories of light in the uniform acceleration elevator and the trajectories of the light in the earth’s Gravitational field are not the same, the deflection effect of the light can not be ignored in the uniform acceleration elevator.
, the trajectories of light in the uniform acceleration elevator and the trajectories of the light in the earth’s Gravitational field are not the same, the deflection effect of the light can not be ignored in the uniform acceleration elevator.
![]()
Figure 2. The deflection angle of light in the acceleration elevator.
Einstein pointed out that in uniform acceleration elevator the propagation path of the light is curved. The observer inside the elevator may think that the bending of light is caused by gravity, and for the observer outside the elevator, the light still travels in a straight line. But because of acceleration movement of the elevator, in this period of time when the photons from the incident point reach the opposite wall, the position of the elevator has changed, so the illumination point of the light on the opposite wall is slightly lower than the point ![]() [1] . According to Einstein’s ideas, let’s estimate the deflection angle of the light in the uniform acceleration elevator.
[1] . According to Einstein’s ideas, let’s estimate the deflection angle of the light in the uniform acceleration elevator.
Assuming that there are three external light pulses along the direction parallel to the floor of the elevator, orderly get in from the point ![]() of the elevator, and after 10 ns get to the opposite wall. The 1st light pulse gets in at time
of the elevator, and after 10 ns get to the opposite wall. The 1st light pulse gets in at time ![]() and gets to the point
and gets to the point ![]() of the opposite wall at time
of the opposite wall at time![]() . The 2nd light pulse gets in at time
. The 2nd light pulse gets in at time ![]() and gets to the point
and gets to the point ![]() of the opposite wall at time
of the opposite wall at time![]() . The 3rd light pulse gets in at time
. The 3rd light pulse gets in at time ![]() and gets to the point
and gets to the point ![]() of the opposite wall at time
of the opposite wall at time![]() . Obviously the following relationship is established:
. Obviously the following relationship is established:
![]()
For ease of calculation, set![]() , then the distance between the point
, then the distance between the point ![]() and the point
and the point ![]() can be obtained as below:
can be obtained as below:
![]() (2)
(2)
In the same way, the distance between the point ![]() and the point
and the point ![]() can be obtained as below:
can be obtained as below:
![]() (3)
(3)
And the distance between the point ![]() and the point
and the point ![]() can be obtained as below:
can be obtained as below:
![]() (4)
(4)
In the General Theory of Relativity, the bending of the light reflects the bending of the space. If the space-time relationship between the accelerating system and the gravitational field is exactly equivalent, the observers in the acceleration elevator will also find that the trajectories of the three light beams from outside are completely coincident, and the three points![]() ,
, ![]() and
and ![]() are at the same position. But the formulas (2)-(4) tell us that the points
are at the same position. But the formulas (2)-(4) tell us that the points![]() ,
, ![]() and
and ![]() are not at the same position. Now let’s calculate the deflection angle of the light in the elevator, because the deflection angle is very small, so
are not at the same position. Now let’s calculate the deflection angle of the light in the elevator, because the deflection angle is very small, so![]() , the deflection angle of the 1st beam is:
, the deflection angle of the 1st beam is:
![]() (5)
(5)
The deflection angle of the 2nd beam is:
![]() (6)
(6)
The deflection angle of the 3rd beam is:
![]() (7)
(7)
∙∙∙, ∙∙∙
The deflection angle of the nth beam is:
![]() (8)
(8)
In the case of![]() ,
, ![]() , so
, so
![]() (9)
(9)
In formula (9), ![]() is the instantaneous speed of the elevator at
is the instantaneous speed of the elevator at ![]() time. According to formula (9), as time goes on, the speed
time. According to formula (9), as time goes on, the speed ![]() will be faster and faster, the deflection angle
will be faster and faster, the deflection angle ![]() of the light will be bigger and bigger in the uniform acceleration elevator,.
of the light will be bigger and bigger in the uniform acceleration elevator,.
Comparing Figure 1(a) and Figure 2, you could find that the light propagation characteristics in the uniform acceleration elevator and the light propagation characteristics in the gravitational field are not the same. When the elevator is parked on the surface of the planet, each light pulse from the point ![]() of the elevator always gets to the point
of the elevator always gets to the point ![]() on the opposite wall. This shows that the deflection angle of every beam is identical. But the three light pulses from the point
on the opposite wall. This shows that the deflection angle of every beam is identical. But the three light pulses from the point ![]() of the uniform acceleration elevator get to the three different points:
of the uniform acceleration elevator get to the three different points:![]() ,
, ![]() and
and![]() . This shows that the deflection angles of the three beams are different in the elevator reference system. So in the Figure 2 the author draws the three different deflection angles:
. This shows that the deflection angles of the three beams are different in the elevator reference system. So in the Figure 2 the author draws the three different deflection angles:![]() ,
, ![]() and
and![]() . According to formulas (5)-(7), the three deflection angles have the following relationship:
. According to formulas (5)-(7), the three deflection angles have the following relationship:
![]() (10)
(10)
The deflection of light in the gravitational field is not the same as it in the uniform acceleration elevator. So the observer in a closed elevator will know that the elevator is parked on the surface of a planet or in the uniform acceleration movement by observing the light coming from outside, even if he does not look outside. If the light in an elevator is curving and the deflection angle of every beam is coincident or the illumination point on the opposite wall is changeless, it shows that the elevator is parked on the surface of a planet. However, if the light in an elevator is curving, but as time goes on, the deflection angle of light will become bigger and bigger, and the illumination point on the opposite wall is moving down constantly, it shows that the elevator is in the uniform acceleration movement.
According to formulas (2)-(4) and (9), under the condition of![]() , the author figures out the downward distance from the illumination point and the deflection angle of the light when the elevator continues to accelerate 1 s, 10 s, 100 s and 600 s. The results are listed in Table 1.
, the author figures out the downward distance from the illumination point and the deflection angle of the light when the elevator continues to accelerate 1 s, 10 s, 100 s and 600 s. The results are listed in Table 1.
It is not difficult theoretically to use experiments to verify the deflection of light in an acceleration system. Let a small rocket continue a uniform accelerated flight for a period of time. The outside light gets into the rocket from the point![]() . Through the photosensitive device on the opposite wall we can detect if the illumination point of the light is constantly moving down, and if the deflection angle of the light is becoming bigger and bigger. If the instrument inside the rocket can detect that the light spot is constantly moving down, it shows that the deflections of the light in a uniform accelerated rocket and in a gravitational field are different. The relationship between the acceleration system and the gravitation field is not completely equivalent.
. Through the photosensitive device on the opposite wall we can detect if the illumination point of the light is constantly moving down, and if the deflection angle of the light is becoming bigger and bigger. If the instrument inside the rocket can detect that the light spot is constantly moving down, it shows that the deflections of the light in a uniform accelerated rocket and in a gravitational field are different. The relationship between the acceleration system and the gravitation field is not completely equivalent.
Because the acceleration of the rocket is only 10 m/s2, so the Space-time curvature effect of the General Theory of Relativity can be ignored; after a sustained acceleration of 600 seconds, the speed of the rocket is only 6 km/s, so the length contraction effect of the Special theory can be ignored. So when calculating the data in Table 1, the author did not consider the effect of the length contraction and Space-time curvature.
2.2.2. The Trajectory of the Photon in the Uniform Acceleration Elevator
In the above example, because the width of the elevator was only 3 m, so when we calculated the deflection angle of the three beams, three curves were replaced by three straight lines. In this section, we will draw out the three curves precisely, thus people can understand that the real trajectories of the photon.
In Figure 3, we used a dashed frame to represent the uniform acceleration elevator, and established a rectangular coordinate system K in the elevator. ![]() is the origin of the coordinate system, the positive direction of x axis points to right of the elevator, Its coordinate unit is
is the origin of the coordinate system, the positive direction of x axis points to right of the elevator, Its coordinate unit is![]() ; the positive direction of y axis points to the above the elevator, Its coordinate unit is
; the positive direction of y axis points to the above the elevator, Its coordinate unit is![]() . The time needs for photons to go through a distance of 3 meters is approximately 10 ns. So we take 10 interval points, set 1 ns as a time interval, and calculate the coordinate values of these three light pulses in each interval, which we needed when drawing out these motion curves of the photons.
. The time needs for photons to go through a distance of 3 meters is approximately 10 ns. So we take 10 interval points, set 1 ns as a time interval, and calculate the coordinate values of these three light pulses in each interval, which we needed when drawing out these motion curves of the photons.
In 1 ns time, the photon pass through 30 cm; in 2 ns time, the photon pass 60 cm; and so on. So the x coordinate values of the three curves are very easy to calculate, and the calculation of y coordinate value can refer to formula (2)-(4). The whole calculation process is not described in detail, here we only list the calculation results: the data of the first curve is in the Table 2, the data of the second curve is in the Table 3, the data of the third curve is in the Table 4.
![]()
Table 1. Downward distance and deflection angle of photon in acceleration system.
![]()
Table 2. The data of the first curve.
![]()
Table 3. The data of the second curve.
![]()
Table 4. The data of the third curve.
In above three tables, the x coordinate unit is![]() , the y coordinate unit is
, the y coordinate unit is![]() . The time internal is 1 ns, namely:
. The time internal is 1 ns, namely:
![]()
According to the data in above three tables, we draw out three curves accurately in Figure 3:![]() ,
, ![]() ,
,![]() . The curve
. The curve ![]() is the trajectory of the first light pulse in uniform acceleration elevator, the curve
is the trajectory of the first light pulse in uniform acceleration elevator, the curve ![]() is the trajectory of the second light pulse, the curve
is the trajectory of the second light pulse, the curve ![]() is the trajectory of the third light pulse.
is the trajectory of the third light pulse.
Comparing Figure 1(b) and Figure 3, people could find that each light pulse from the point ![]() of the stationary elevator always gets to the point
of the stationary elevator always gets to the point ![]() on the opposite wall in the gravitational field, the path of every beam is identical, and the irradiation point is constant, so the author draw only a curve
on the opposite wall in the gravitational field, the path of every beam is identical, and the irradiation point is constant, so the author draw only a curve ![]() and a point of illumination
and a point of illumination ![]() in Figure 1(b); but three beams from the point
in Figure 1(b); but three beams from the point ![]() of the uniform acceleration elevator, the paths of the three beams are different, so in Figure 3 there were three completely separate curves
of the uniform acceleration elevator, the paths of the three beams are different, so in Figure 3 there were three completely separate curves![]() ,
, ![]() ,
, ![]() and locations with different illumination points
and locations with different illumination points![]() ,
, ![]() ,
, ![]() , as time goes on, the trajectory of the light became more and more curved. Figure 3 once again proved: The deflection of the light in the uniform acceleration elevator is different from the deflection of the light in the gravitational field, there are not completely equivalent relationship between the uniform acceleration elevator and the gravitational field.
, as time goes on, the trajectory of the light became more and more curved. Figure 3 once again proved: The deflection of the light in the uniform acceleration elevator is different from the deflection of the light in the gravitational field, there are not completely equivalent relationship between the uniform acceleration elevator and the gravitational field.
3. Uniform Rotating Disc and Gravitational Field Are Not Completely Equivalent
Suppose that there is a room on the surface of a planet, and a sagging spring connects a small ball ![]() whose quality is
whose quality is ![]() to the roof. The ball is subjected to two forces: one is the upward spring pull, and the other is the downward gravitational force. The two forces balance, and the ball
to the roof. The ball is subjected to two forces: one is the upward spring pull, and the other is the downward gravitational force. The two forces balance, and the ball ![]() is in a stationary status in the room. Suppose again that
is in a stationary status in the room. Suppose again that
![]()
Figure 3. The bending light in the acceleration elevator.
there is a disc in a so-called free space, and a spring connects a small ball ![]() whose quality is
whose quality is ![]() to the center of the disc. When the disc uniform rotation, the ball is also subjected to two forces: One is the spring pull toward the center of the disc, and the other is the centrifugal force opposite to the direction of the spring pull. According to the analysis on the forces of the small ball in the disc reference frame, the spring pull and the centrifugal force balance, and the ball
to the center of the disc. When the disc uniform rotation, the ball is also subjected to two forces: One is the spring pull toward the center of the disc, and the other is the centrifugal force opposite to the direction of the spring pull. According to the analysis on the forces of the small ball in the disc reference frame, the spring pull and the centrifugal force balance, and the ball ![]() is in a stationary status in the disc. So Einstein believed that the centrifugal force and the gravitation force are equivalent.
is in a stationary status in the disc. So Einstein believed that the centrifugal force and the gravitation force are equivalent.
An observer on the disc may think that the disc is stationary, and the small ball is subject to the forces of gravitation and bounce. The two forces balance so that the ball is in a stationary status. Modern physicists generally believe that the uniform rotating disc and the gravitational field are completely equivalent. If the disc is enclosed, the observer on the disc will never be able to use any experiment to distinguish between the centrifugal force and the gravity.
But in fact, it is not the truth. Even if the disc is enclosed, the observer can still distinguish between the centrifugal force and the gravity in free fall experiments of objects. As long as cutting off the spring connecting the roof and the small ball, the observer in the room will see that the ball goes into the free fall status under the action of gravity. The direction of the free fall is consistent with the direction of the gravity. In the whole process of falling, the speed of an object is getting faster and faster, thus the kinetic energy is getting bigger and bigger. But on the uniform rotating disc this scene can’t be sawn. At the moment the spring is cut off, the ball will not do the free fall movement in the direction of the centrifugal force, but will fly away instead at the original speed along the direction of tangent line of the circular motion. If the closed disc is large enough, the observer will find that the moving path of the ball is a spiral line and the kinetic energy of the flying ball is constant. On the surface of a planet, an object will do free fall movement under gravity action, but on a uniform rotating disc, it is not possible for an object to do the free fall movement under centrifugal force action. According to this, the observer on the disc can distinguish between gravity and centrifugal force. It shows that the uniform rotating disc and the gravitational field are not completely equivalent.
4. Think about Time Property of Acceleration System and Gravitational Field
According to the General Theory of Relativity, the intensity of the gravitational field affects the rhythm of the clock. The bigger the gravity, the slower the clock goes. Based on the principle of equivalence, some physicists have come to the conclusion that the more the acceleration is, the more the time expands [2] . But experiments show that acceleration has no effect on the clock rhythm. The most classical experiment to verify the time dilation is to observe the average life span of various kinds of mesons. These experiments can be done in two ways. One is through the observation of cosmic rays from outer space. The mesons of cosmic rays are in a uniform linear motion. The other is to put the meson in a cyclotron and to make it do uniform circular movement. According to the saying: “the more accelerated, the more delay”, the meson in cyclotron will have more delays because it has more acceleration movement than the meson in the cosmic ray. But the experiment tells us that whether the meson is making a uniform linear motion or making a uniform circular motion, time dilation is only related to the speed of the clock, and there is no correlation between the acceleration and the time dilation.
Suppose that a meson is in a uniform circular motion in a cyclotron. If the acceleration does affect the rhythm of the clock, as long as the radius of the circular motion of the meson is shortened, under the condition of constant line speed, the average life will be extended. But that never happened. By further analysis of these experiments you will also find that even in the case of 1016 g acceleration, it does not produce any impacts on the clock rate [3] . According to the General Theory of Relativity, the intensity of the gravitational field affects the rhythm of the clock, and according to the results of experiments, the intensity of the acceleration field does not affect the rhythm of the clock. It shows that the acceleration system and the gravitational field is not completely equivalent.
5. Conclusions
The author makes some analysis on the equivalence of the acceleration system and the gravitational field, and the results are as follows:
1) According to the author’s estimate, the deflections of light in the gravitational field and in the uniform acceleration elevator are not consistent, the uniform acceleration elevator and the gravitational field are not completely equivalent.
2) The object can go into the free fall under the action of gravity, but the centrifugal force on a uniform rotating disc does not have the function. This shows that the uniform rotating disc and the gravitational field are not completely equivalent.
3) According to the General Theory of Relativity, the intensity of the gravitational field affects the rhythm of the clock. In a place where the gravity is bigger, the clock goes more slowly. But in the experiment, it was discovered that acceleration had no effect on the clock rhythm. Even when the acceleration reached 1016 g, it is still the case. This shows that the time-space relationship between the acceleration system and the gravitational field is not completely equivalent.
4) In the book “Analysis of Relativity Theory” published in 2015, the author carefully thinks about the equivalence relationship between the uniform rotating disc and the uniform acceleration elevator, and gets to the conclusion that there is only a partial equivalence in the acceleration systems and in the gravitational field. There is no completely equivalent relationship [4] .
5) The principle of equivalence is an extremely important principle in modern physics. If there are several experiments which can prove that the gravitational field and the accelerating system are not completely equivalent, it will lead to a major change in Physics.