Reliability Design of Ice-Maker System Subjected to Repetitive Loading ()
1. Introduction
Reliability describes the ability of a system or module to function under stated conditions for a specified period of time [1] . If a refrigeration system or a major component in the systems such as an ice-dispensing machine was to exhibit the failure profile in the bathtub curve with a large number of failures in the early life of its introduction, it would be difficult for the system to be successful in the marketplace. Improving the reliability of a system or component through systematic testing should reduce its failure rate from the traditional failure rate typified by the bathtub curve to the failure rate represented by a flat, straight line with the shape parameter β in Figure 1. With the second curve, there are low failure rates throughout the lifetime of the system or component until reaching the end of its useful life when the failure rate begins to increase.
The product reliability function can be quantified from the expected product lifetime LB and failure rate l in Figure 1 as follows:
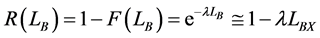 (1)
(1)
This equation is applicable below about 20 percent of cumulative failure [2] . If one module of refrigeration such as ice-maker malfunctions, consumers will request that the module be replaced. If the field usage patterns are fully understood from the returned product, the laboratory could reproduce the usage patterns and failures found in the field.
However, it may not be easy to identify all failure modes attributable to the particular design because the failure modes in the mechanical systems come from repetitive stresses which may not be found in its initial testing or design. Refrigeration system modules such as ice-maker system need to be robustly designed to withstand a variety of loads. Consequently, the ice-maker system determines the control factors (or design parameters) to endure the noise factors (or stresses) so the system properly works. Such reliability targeting is known to be conventionally achieved through the Taguchi methods (SDE) and the statistical design of experiment [3] - [8] . However, for a simple mechanical structure, the Taguchi methods’ robust design process might consider a large number of design parameters and is hard to determine the design parameters.
In this study we present a new parametric Accelerated Life Testing (ALT) method that can improve the reliability of fractured helix upper dispenser in field. This new accelerated testing methodology [9] - [22] takes into account the fact that the ice-maker system with missing or improper design parameters can result in recalls and loss of brand name value. Based on the failure analysis of a fractured helix upper dispenser, we demonstrate the validity of our new reliability design method. The method uses parametric ALT and new sample size equations as a novel means of determining proper
![]()
Figure 1. The bathtub curve and straight line with slope b.
design parameters.
2. Failure Analysis of Helix Upper Dispenser in an Ice-Maker System
As seen in Figure 2, the basic function of a refrigerator is to store fresh and/or frozen foods. Refrigerators today provide other functions, such as dispensing ice and water. As the number of refrigerator functions and their parts increase, product reliability can be required; Market pressure for cost reduction leads to the use of cheaper parts.
In the marketplace, one part in ice-maker system was cracking or fracturing (see Figure 3). The patterns of customer usage were unknown. To prevent the massive recalls in field, it is a critical process to know why this crack happens immediately.
An ice-maker system in a refrigerator consists of multiple parts―AC auger motor, ice bucket, ice tray, and lever. They can be put together as a subassembly and have an
![]()
Figure 2. Breakdown of a refrigeration system with its modules, components, and parts.
![]()
Figure 3. Refrigeration System lifetime LB and failure rate λs with modules.
input and output for ice harvest. As parameters and required input, robust design schematic of ice-maker employs two experimental arrays: one for the control array (design) and the other for the noise array (loads). Optimizing over the control factors, optimal design data can be reduced to a signal (output)-to-noise (load) ratio. As there are multiple parts in ice-maker system, ultimately, it is designed to harvest ice (see Figure 4).
Where these parts might receive mechanical overloads in ice-making process, there are two cases―the crushed or fused ice. Depending on the customer usage conditions, the mechanical load of the icemaker is low because it is operated without fused or webbed ice. Fused or webbed ice will form in the tray when they do not dispense ice in cubed mode for long time.
Another case is crushed ice. It involves several kinematic or mechanical processes: 1) the filtered water is pumped through a tap line that is supplying the ice tray; 2) the cold air in the heat exchanger chills the tray; 3) after ice is made, the cubes are harvested, stocking the bucket until it is full; and 4) a crusher breaks the cubed ice in the crushed mode. When the customer pushes the lever by force, the crushed ice is dispensed in its mode.
Figure 5 shows a power flow of the mechanical load transfer in the ice-maker assembly and its bond graph modeling in the process of ice-making. An AC auger motor generates enough torque to crush the ice. Auger motor power is transferred through the gear system to the ice bucket assembly―that is, to the helix upper dispenser, the blade dispenser and the ice crusher.
The bond graph can be conventional in state space representation to group terms by state variables. The modeling (or state equation) of ice bucket assembly can be expressed as
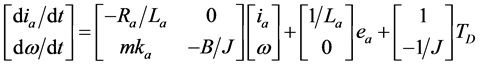 (2)
(2)
The mechanical stress of the ice bucket assembly depends on the disturbance load TD in Equation (2).
If there is a void such as structural design flaw - 2 mm gap and weldline where the
![]()
Figure 4. Robust design schematic of ice-maker system.
![]() (a)
(a)![]() (b)
(b)
Figure 5. A power flow of ice-maker assembly and its bond graph modeling. (a) A power flow of ice-maker assembly; (b) Bond-graph modeling.
loads are applied, the structure subjected to repetitive stress can fracture at that location (see Figure 6). The failure mechanisms of helix upper dispenser in ice-maker system can be fracture or crack. The failure site of the mechanical structure such as helix upper dispenser might be identified when the failed products are taken apart in the field or could be after parametric ALT is carried out.
Failure of helix upper dispenser can happen when the strength of materials composing the system structures yield with the loads applied to it. The load could be higher than the system was designed for or the material could be insufficient to handle repetitive loads to which it is subjected. That is, failure occurs when the stress is greater than the material strength, or when the material cannot withstand the loads.
The design engineer would want to move the void in the structure to a location away from where the stress (or load) is applied. A reliability engineer should seek to redesign the structure to either: 1) move the loads, or 2) change the material shape and type to withstand the load.
To derive the life-stress model for helix upper dispenser, the time to failure (TF) can be estimated from the McPherson’s derivation [23] :
 (3)
(3)
![]()
Figure 6. Structure of helix upper dispenser.
The first term on the right hand side of Equation (3) is the load and the second term is the internal energy. The internal (or external) stress in a product is difficult to quantify and use in accelerated testing. It is necessary to modify Equation (3) into a more applicable form. Thus, stresses in crushing ice may come from the torque. Because there is no temperature change, its portion of second term can be neglected.
From the time-to-failure in Equation (3), the acceleration factor can be defined as the ratio between the needed accelerated stress levels and those found under typical operating conditions. The acceleration factor (AF) can be modified to include the load from Equation (3):
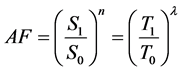 (4)
(4)
Under severe testing (or accelerated) conditions, the refrigeration system subjected to a duty cycle will experience a shortened module lifetime [24] .
3. Parametric Accelerated Life Testing in Ice-Maker System
As seen in Figure 7, refrigerator consists of multiple modules, component, and parts. If one part subjected to loads has design problems, module structure will be broken in field. An ALT plan can be developed to reproduce a problematic component or module of the system that has a high failure rate or short life in field. This plan, if implemented properly in parametric ALT, can reduce failure rates and improve reliability.
In targeting the reliability of the refrigerator, there are three cases: the new design maintains a modified module, new module, and similar module to the prior design on the basis of market data. Ice-maker module is indeed the modified one to the prior design because design flaws―2 mm gap and weldline will be eliminated. In targeting the reliability of the modified module, the field data are often used as a reference.
Like module D listed in Table 1, ice-maker system from the field data was that the
![]()
Figure 7. Breakdown of a refrigeration system with its modules, components, and parts.
![]()
Table 1. Overall parametric ALT plan of Refrigerator.
yearly failure rate was 0.31%/year and lifetime, LB1 was 3.2 years. To respond a customer claims, new target for ice-maker system was set to be LB1 10 years with 1.0 yearly failure rate and the ice-maker system is determined by the lifetime of the helix upper system.
To derive the sample size equation, probability concept in reliability engineering should be understood. The Cumulative Distribution Function (CDF) in the Weibull function can be expressed as:
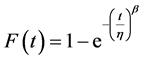 (5)
(5)
The Weibull reliability function, R(t), is expressed as:
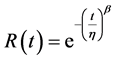 (6)
(6)
The characteristic life hMLE from the Maximum Likelihood Estimation (MLE) can be derived as:
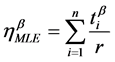 (7)
(7)
If the confidence level is 100(1 - a) and the number of failures, r, is expected to be r ³ 1, then the characteristic life, ha, can be estimated from Equation (14):
 (8)
(8)
Presuming there are no failures, the p-value is a and ln(1/a) is mathematically
equivalent to the Chi-Squared value,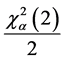 . The characteristic life ha, would then be represented as:
. The characteristic life ha, would then be represented as:
![]() (9)
(9)
Equation (8) is established for all cases r ³ 0 and can be redefined as follows:
![]() (10)
(10)
To evaluate the Weibull reliability function, the characteristic life can be converted into LB life as follows:
![]() (11)
(11)
After a logarithmic transformation, Equation (11) can be expressed as:
![]() (12)
(12)
If the estimated characteristic life of p-value a, ha, in Equation (10), is substituted into Equation (12), we obtain the BX life equation:
![]() (13)
(13)
Because most accelerated lifetime testing typically has a small number of samples, the number of failures would not be as much as that of the sample size.
![]() (14)
(14)
If Equation (14) is substituted into Equation (13), the BX life equation becomes an inequality and can be written as follows:
![]() (15)
(15)
The sample size equation with the number of failures can also be modified as follows:
![]() (16)
(16)
For a 60% confidence level, the first term, ![]() , in Equation (23) can be approximated as (r + 1) [25] . In addition, if the cumulative failure rate, x, is below about 20 percent, the denominator of the second term,
, in Equation (23) can be approximated as (r + 1) [25] . In addition, if the cumulative failure rate, x, is below about 20 percent, the denominator of the second term, ![]() , can be approximated as x by
, can be approximated as x by
a Taylor expansion. These approximations transform the general sample size equation to the following:
![]() (17)
(17)
If the acceleration factor, AF, from Equation (4) is added into the planned testing time, Equation (24) can be modified to include AF. When the target reliability ? failure rate l and lifetime LB are given, this equation will be used to carry out parametric accelerated life testing:
![]() (18)
(18)
4. Laboratory Experiments
Generally, the operating conditions for the mechanical ice bucket assembly in an icemaker are −15˚C to −30˚C temperature, 0% - 20% relative humidity, and 0.2 - 0.24 G vibration.
The dispenser is used an average of approximately 3 - 18 times per day in the United States. Under maximum use for 10 years, the dispenser incurs about 65,700usage cycles (![]() ). Data from the motor company specifies that normal torque is 0.69 kN cm and maximum torque is 1.47 kN cm. Assuming the quotient n = 2 (or the cumulative damage exponent l = 2), the acceleration factor is approximately 5 in Equation (4).
). Data from the motor company specifies that normal torque is 0.69 kN cm and maximum torque is 1.47 kN cm. Assuming the quotient n = 2 (or the cumulative damage exponent l = 2), the acceleration factor is approximately 5 in Equation (4).
Assume that the shape parameter was 2, the test cycles and the numbers of samples calculated from Equation (18) were 42,000 cycles and 10 pieces, respectively. The parametric ALT for helix upper dispenser was designed to ensure a B1 of 10 years life with about a 60% level of confidence that it would fail less than once during 42,000 cycles.
Figure 8 shows the ALT equipment that is designed to apply the helix upper dispenser to the disturbance load TD and its duty cycle. The equipment in the chamber was designed to operate to about −30˚C of temperature. The controller outside can start or stop the equipment and indicate the completed test cycles, and the test periods, such as sample on/off time.
When the controller outside the chamber gives the start signal, the auger motor rotates the clamp helix dispenser, the helix upper dispenser and the blade dispenser. To apply the maximum disturbance torque TD, two parts―the helix upper dispenser and the band clamper―were bolted together to slip them. At this point, the rotating blade dispenser will impact the fixed helix upper dispenser to the maximum mechanical disturbance torque (1.47 kN・cm). Depending on the operating condition of the equipment, the blade dispenser will provide maximum torque to the helix upper dispenser 4 - 6 times in 5 seconds.
5. Results and Discussion
Figure 9 shows the failed product in the field and a sample after accelerated life testing. In the photo, the shape and location of the broken pieces in the failed market product are identical to those in the ALT results. Figure 10 represents the graphical analysis of the ALT results and field data on a Weibull plot. For the shape parameter, the estimated
![]() (a)
(a)![]() (b)
(b)
Figure 8. Equipment for the compressor accelerated life tests and its duty cycle. (a) Parametric ALT Equipment; (b) Duty cycles on the ALT equipment.
![]() (a) (b)
(a) (b)
Figure 9. Failure of helix upper dispenser from the field and an ALT. (a) Failed valve from the field; (b) Failed valve from an ALT.
![]()
Figure 10. Field data and results of accelerated life test on Weibull chart.
value in the previous ALT is 2.0. However, the final value confirmed on the Weibull plot was 4.8. As the ratio of characteristics life, h1/h2, gives the acceleration factor, AF is approximately 2.2 on the Weibull plot.
We conclude that these methodologies are valid to reproduce the fielded failures because (1) the location and shape of the fractures in both market and ALT results are extremely similar; and (2) on the Weibull plot, the shape parameters of the ALT results, b1 and market data, b2, are very similar. It also might represent the load states in field and parametric ALT. This approach was very effective in reproducing the fracture of the product from the marketplace.
The fracturing and cracking of both the fielded products and the ALT results occur in the contact area of the blade dispenser, where was the design flaw―2 mm gap. Due to the design defects between the blade dispenser and helix upper dispenser, the impact (1.47 kN×cm) of the blade dispenser generated the high stress against the helix upper dispenser. The concentrated stress of the blade dispenser is approximately 36.9 kPa, based on finite element analysis (FEA). When the blade dispenser, made of stainless steel, meets the polycarbonate helix upper dispenser at a right angle in −30˚C, it will be fractured near the impact area of the helix upper dispenser.
Based on failure analysis and first ALT, the design flaw―2 mm gap was the root cause of the fractured helix upper dispenser in ice-maker system. The missing design parameters for the helix upper dispenser were modified as follows: 1) the design flaws (C1: gap reduction, 1.2 → 0.0 mm), 2) the shape of blade dispenser (C2), and 3) the weld line (C3) (see Figure 11). When the gap between blade dispenser and helix upper dispenser was eliminated in this modified design, the mechanical concentrated stress of the sample, based on finite element analysis, was reduced from 36.9 kPa to 21.3 kPa.
All samples in the first ALT (n = 10) failed within 11,600 cycles as shown in Table 2. The reliability quantitative test specifications (RQ) of a mechanical structure does not meet that newly designed samples do not fail within the target life of B1 10 years. The confirmed values of AF and b in Figure 10 were 2.2 and 4.8 (See Figure 10).
For the second ALT, the test sample number and required testing cycles recalculated in Equation (18) was 6 pieces and 54,000 cycles. In result all samples were failed within 38,000 cycles, as shown in Table 2. The missing design parameters for the helix upper dispenser in ice-maker system were modified to add ribs on the side and front of the impact area (C4). The reliability quantitative test specifications (RQ) of a mechanical structure does not meet that newly designed samples do not fail within the target life of B1 10 years.
In the third ALT results, the samples did not crack and fracture until 75,000 cycles of parametric ALT. The reliability quantitative test specifications (RQ) of a mechanical structure meet that newly designed samples do not fail within the target life of B1 10 years. The design improvements of eliminating the gap and reinforcing the ribs were very effective in enhancing the reliability of the sample (see Table 2). Figure 12 also
![]() (a) (b)
(a) (b)
Figure 11. Redesigned helix upper dispenser. (a) Initial design; (b) Modified design.
![]()
Table 2. Overall parametric ALT plan of Refrigerator.
![]()
Figure 12. Result of ALTs plotted in Weibull chart.
shows the graphical results of an ALT plotted in a Weibull chart.
6. Conclusions
To improve the reliability of ice-maker system with the fractured helix upper dispenser in field, we have examined the failure analysis for fractured helix upper dispensers and carried out the parametric ALTs with various design improvements. The following general conclusions were obtained:
1) Based on the claimed marketplace product returns and ALT reproduction, the root causes of ice-maker system with the failed helix upper dispenser in field came from the fragile structure of the helix upper dispenser. Specific flaws were found to be 2 mm gap, the weldline, and the impact of the stainless steel blade dispenser on the polycarbonate helix upper dispenser.
2) The critical controllable design improvements involved gap elimination and rib reinforcement. These were shown to be effective in enhancing the reliability of ice- maker system with the helix upper dispenser fractured in field.
3) After a sequence of parametric ALTs, the samples did not crack and fracture until 75,000 cycles of parametric ALT. The reliability quantitative test specifications (RQ) of a mechanical structure meets because newly designed samples do not fail within the target life of B1 10 years.
4) The failure analysis of the failed product and three rounds of ALT were very effective in reproducing the ice-maker system with the fractured helix upper dispenser claimed in the marketplace and in improving its reliability.
The new reliability design methodology could be applied to other mechanical systems, including automobile gear trains and engines, construction equipment, forklifts, washing machines, vacuum cleaners, and motor fan systems. We recommend that the missing or improper controllable design parameters on these systems should be studied for reliability design. These parameter studies might include failure analysis, load analysis, and a tailored series of accelerated life tests.