Optimal Multiperiodic Control for Inventory Coupled Systems: A Multifrequency Second-Order Test ()
1. Introduction
We consider complex autonomous inventory coupled (IC) systems. Such systems can take, for example, the form of a network of chemical or biochemical networks, where the inventory interactions perform the recycling of by-products or by-streams from some subsystems to other subsystems as their input components or energy carriers [1] . Because of the flexible interactions of the subsystems, each of them can be operated with their own period utilizing advantageously its dynamic properties. In this context, we formulate the multiperiodic optimal control problem, which generalizes the periodic control approach finding much attention for the optimization of chemical and biotechnological processes [2] - [6] . We analyze three kinds of operation for IC systems: the steady state one, the periodic one, and the multiperiodic one with possibly incommensurate operation frequencies of the subsystems. We develop a multifrequency second- order test, which can be used to ensure the best intensification of the productivity of IC systems preserving at the same time their advantageous ecological features: many by- products are recycled within a complex system. The justification of the test proposed is obtained by the approach avoiding the regularity conditions, which generalizes such an approach for single systems. We illustrate the theoretical considerations by the example of multiperiodic optimization of a complex chemical production system.
Notation: 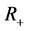 is the set of positive reals;
is the set of positive reals; 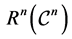 is the space of n-dimensional real (complex) vectors x with the norm
is the space of n-dimensional real (complex) vectors x with the norm ;
; ;
; 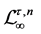 is the space of t-periodic n-dimensional essentially bounded functions x equipped with the norm
is the space of t-periodic n-dimensional essentially bounded functions x equipped with the norm ;
;  is the space of t-periodic n-dimensional functions with the essentially bounded derivative and the norm
is the space of t-periodic n-dimensional functions with the essentially bounded derivative and the norm 
 is the zero (the identity) matrix of the dimension
is the zero (the identity) matrix of the dimension 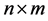 (
(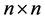 );
); is the interior of the set X;
is the interior of the set X;  is the dimension of a variable x;
is the dimension of a variable x;  for
for ;
;  is the set of t-periodic n-dimensional trigonometric polynomials of degree
is the set of t-periodic n-dimensional trigonometric polynomials of degree ; and
; and  is the average value of a t-periodic function
is the average value of a t-periodic function![]() .
.
2. Optimal Multiperiodic Control Problem
Consider the following optimal multiperiodic control problem for IC systems (the problem M) composed of the set ![]() of N subsystems: find for each subsystem its operation period
of N subsystems: find for each subsystem its operation period![]() , and its
, and its ![]() -periodic control process
-periodic control process ![]() encompassing its
encompassing its ![]() -periodic state trajectory
-periodic state trajectory![]() , its
, its ![]() -periodic extended control
-periodic extended control![]() , which minimize the performance index
, which minimize the performance index
![]() (1)
(1)
being a scalar function of the ![]() -averaged outputs of the subsystems
-averaged outputs of the subsystems
![]() (2)
(2)
and subject to the resource-technological constraints of the subsystems
![]() (3)
(3)
the state equations of the subsystems
![]() (4)
(4)
the inventory constraints
![]() (5)
(5)
and the box constraints for the process variables
![]() (6)
(6)
where the extended control ![]() of the ith subsystem encompasses its local control
of the ith subsystem encompasses its local control![]() , and its inventory control
, and its inventory control![]() , and
, and![]() , and
, and![]() are the box sets, and
are the box sets, and
![]()
![]()
![]()
while ![]() is the multiperiodic control process of the IC system. We denote the set of all such processes satisfying the constraints (2)-(6) with a fixed multiperiod
is the multiperiodic control process of the IC system. We denote the set of all such processes satisfying the constraints (2)-(6) with a fixed multiperiod ![]() by
by![]() , and the corresponding problem
, and the corresponding problem ![]() by
by![]() .
.
The objective function (1) represents the global benefits from the multiperiodic operation of the IC system, which are determined with the help of the ![]() -averaged outputs (2) of the subsystems depicting, for example, their averaged production performance or their averaged selectivity. The constraints (3) mirror the averaged availability of the resources used for the process operation, and the technological requirements for the averaged product purity. The inventory interactions (5) perform the recycling of by-products or by-streams of some subsystems to other subsystems as their input components or energy carriers [1] . Because of the flexible interactions of the subsystems each of them can be operated with their own period utilizing advantageously its dynamic properties, which leads to the nested multiperiodic optimization encompassing the static and periodic optimization as its particular cases. The structural matrices
-averaged outputs (2) of the subsystems depicting, for example, their averaged production performance or their averaged selectivity. The constraints (3) mirror the averaged availability of the resources used for the process operation, and the technological requirements for the averaged product purity. The inventory interactions (5) perform the recycling of by-products or by-streams of some subsystems to other subsystems as their input components or energy carriers [1] . Because of the flexible interactions of the subsystems each of them can be operated with their own period utilizing advantageously its dynamic properties, which leads to the nested multiperiodic optimization encompassing the static and periodic optimization as its particular cases. The structural matrices ![]() and
and ![]() determine the averaged constraint of the inventory control of the ith subsystem by the averaged outputs of the other subsystems.
determine the averaged constraint of the inventory control of the ith subsystem by the averaged outputs of the other subsystems.
3. The Multifrequency Second-Order Test for Complex Systems
Constraining the variables ![]() to the steady functions
to the steady functions ![]() we obtain the optimal steady-state problem for the IC systems (the problem S):
we obtain the optimal steady-state problem for the IC systems (the problem S):
![]() (7)
(7)
where ![]() is the steady-state control process of the IC system with the components
is the steady-state control process of the IC system with the components![]() . Let
. Let ![]() be a locally optimal steady-state process of the IC system (the
be a locally optimal steady-state process of the IC system (the ![]() -process) with the components
-process) with the components ![]() (the
(the ![]() -processes).
-processes).
Assumption 1: The functions ![]() and
and ![]() are twice continuously differentiable in some neighbourhoods of the points
are twice continuously differentiable in some neighbourhoods of the points ![]() and
and![]() , respectively
, respectively![]() .
.
Assumption 2: The steady states ![]() are lying in the interior of their box sets, i.e.
are lying in the interior of their box sets, i.e.![]() .
.
Let ![]() be the solution of the differential equation
be the solution of the differential equation
![]()
for the reduced ![]() -periodic control process of the ith subsystem
-periodic control process of the ith subsystem ![]() ,
, ![]() Using the affine scaling of the variables
Using the affine scaling of the variables ![]() we convert the sets
we convert the sets ![]() into the hypercubes
into the hypercubes![]() . We write their box constraints as
. We write their box constraints as![]() , where the functions
, where the functions ![]() take the form take the form
take the form take the form ![]() and
and ![]() .
.
We convert the problem ![]() to the following reduced form (the problem
to the following reduced form (the problem![]() ):
):
![]()
where ![]() is the reduced multiperiodic control process normed as
is the reduced multiperiodic control process normed as![]() . The set of all admissible processes of the problem
. The set of all admissible processes of the problem ![]() is denoted by
is denoted by![]() .
.
The ![]() -process induces a reduced locally optimal steady-state process
-process induces a reduced locally optimal steady-state process ![]() of the problem
of the problem ![]() (the
(the ![]() -process) with the components
-process) with the components ![]() The problem
The problem ![]() is locally proper at
is locally proper at ![]() iff
iff ![]() is not its local minimum.
is not its local minimum.
We approximate the controls ![]() by the trigonometric polynomials
by the trigonometric polynomials ![]() (the T-controls) defined as
(the T-controls) defined as
![]()
with the coefficients ![]() and the operation frequency
and the operation frequency![]() . We denote by
. We denote by ![]() the set of the coefficients of the T-controls
the set of the coefficients of the T-controls
with![]() . We distinguish the subvectors
. We distinguish the subvectors
![]() of the vector
of the vector ![]() connected with its internal part
connected with its internal part ![]() , and its boundary parts
, and its boundary parts ![]() and
and![]() , where
, where ![]() . We fix the control
. We fix the control ![]() on its optimal steady-state level
on its optimal steady-state level![]() , while we shift the controls
, while we shift the controls ![]() to the interior of their box sets. We impose on the subvectors
to the interior of their box sets. We impose on the subvectors ![]() the pure dynamic T-controls
the pure dynamic T-controls ![]() We set
We set![]() . We write the generalized function of the box constraints as
. We write the generalized function of the box constraints as![]() , where the functions
, where the functions ![]() take the form
take the form
![]() for
for ![]() and
and ![]() for
for![]() .
.
We write the multi-trigonometric approximation ![]() of the problem
of the problem![]() :
:
![]()
where the mappings ![]() determining the con- straints on the T-controls are defined as
determining the con- straints on the T-controls are defined as
![]()
with
![]()
![]()
![]()
![]()
and ![]() and
and ![]() is the reduced multi-trigono- metric control process of the IC system with the components
is the reduced multi-trigono- metric control process of the IC system with the components ![]() . The set of all admissible control processes of the problem
. The set of all admissible control processes of the problem ![]() is denoted by
is denoted by![]() .
.
Assumption 3: The number of points ![]() of the discrete time grid
of the discrete time grid ![]() is coordinated with the degree
is coordinated with the degree ![]() of the trigonometric polynomials
of the trigonometric polynomials ![]() such that
such that![]() .
.
Lemma 1. The ![]() -process and the problems
-process and the problems![]() ,
, ![]() and
and ![]() have the following nesting
have the following nesting![]() , which means that the set of the reduced admissible multi- trigonometric control processes
, which means that the set of the reduced admissible multi- trigonometric control processes ![]() contains the
contains the ![]() -process, and is contained in the set of the reduced admissible multiperiodic control processes
-process, and is contained in the set of the reduced admissible multiperiodic control processes![]() , which can be extended to the set of admissible multiperiodic control processes
, which can be extended to the set of admissible multiperiodic control processes![]() .
.
Proof. The ![]() -process satisfies the constraints
-process satisfies the constraints ![]() by their definition. It also verifies the constraints
by their definition. It also verifies the constraints![]() , since its dynamic parts are nullified
, since its dynamic parts are nullified ![]() and
and ![]() Thus
Thus![]() . The constraints
. The constraints ![]() mean that
mean that![]() , which implies, by the uniform norm evaluation of the T-control [7] [8] , the inequalities
, which implies, by the uniform norm evaluation of the T-control [7] [8] , the inequalities ![]() and
and![]() . The constraints
. The constraints ![]() mean that
mean that![]() , and imply by the same evaluation
, and imply by the same evaluation ![]() On the other hand the constraint
On the other hand the constraint ![]() involves
involves![]() . Hence
. Hence ![]() and
and![]() . Similarly the constraints
. Similarly the constraints ![]() and
and ![]() imply
imply![]() . Thus
. Thus![]() . The latter set can be extended to the set
. The latter set can be extended to the set![]() . W
. W
Let ![]() be the L(agrange)-function for the problem S with
be the L(agrange)-function for the problem S with
![]()
where ![]() is the multiplier connected with the performance index of the problem S, and
is the multiplier connected with the performance index of the problem S, and ![]() and
and ![]() are the multipliers assigned to the constraints
are the multipliers assigned to the constraints ![]() and
and![]() , and
, and ![]() is the multiplier of the problem S with
is the multiplier of the problem S with![]() , and
, and ![]() is the active part of the constraint
is the active part of the constraint ![]() at
at![]() ,
, ![]() is the active part of the constraint
is the active part of the constraint ![]() at
at![]() , and
, and ![]() is the active part of the constraint
is the active part of the constraint ![]() at
at![]() . We set
. We set ![]() .
.
Lemma 2. If ![]() is a local minimum of the problem
is a local minimum of the problem![]() , then there exists a nonzero multiplier
, then there exists a nonzero multiplier ![]() such that the following conditions are satisfied
such that the following conditions are satisfied
![]()
![]() (8)
(8)
Let ![]() be the multipliers for the active constraints
be the multipliers for the active constraints![]() , let
, let
![]()
and let ![]() be the multiplier of the problem
be the multiplier of the problem![]() . We set
. We set![]() ,
,![]() ,
, ![]() , and we write the L-function of the problem
, and we write the L-function of the problem![]() :
:
![]()
We abbreviate the (partial) derivatives evaluated at ![]() as
as
![]()
![]()
![]()
![]()
Assumption 4: The matrices ![]() are nonsingular for all
are nonsingular for all ![]() such that
such that![]() .
.
This assumption eliminates the onset of free, and resonance oscillations in the subsystems.
Lemma 3. The s-process satisfies the FON conditions of the problem ![]() regardless if it is its local minimum or not. These conditions take for a nonzero multiplier
regardless if it is its local minimum or not. These conditions take for a nonzero multiplier ![]() the form
the form
![]()
![]() (9)
(9)
Proof. The problem ![]() can be interpreted as the finite dimensional optimization problem with respect to the argument
can be interpreted as the finite dimensional optimization problem with respect to the argument![]() . The conditions (9) are a consequence of the nullifying of the derivatives
. The conditions (9) are a consequence of the nullifying of the derivatives ![]() and
and![]() . They are satisfied for
. They are satisfied for ![]() and
and ![]() following from the conditions (8). W
following from the conditions (8). W
Thus the FON conditions of the problem ![]() cannot be used to discern improving multiperiodic controls. The second order necessary (SON) conditions exploiting the set
cannot be used to discern improving multiperiodic controls. The second order necessary (SON) conditions exploiting the set ![]() of critical directions can be useful to this end. Because of the averaging operation it may be defined in terms of the variations of the constant components
of critical directions can be useful to this end. Because of the averaging operation it may be defined in terms of the variations of the constant components ![]() of the periodic state trajectories of the subsystems and the variations of their T-controls
of the periodic state trajectories of the subsystems and the variations of their T-controls ![]()
![]()
where ![]()
Let ![]() be the set of the normalized multipliers satisfying the FON conditions (9) of the problem
be the set of the normalized multipliers satisfying the FON conditions (9) of the problem![]() , let
, let ![]() be the set of admissible multiperiods of the IC system, and let
be the set of admissible multiperiods of the IC system, and let ![]() are the subvectors of the complex
are the subvectors of the complex
vector ![]() connected with the internal (
connected with the internal (![]() ) and boundary
) and boundary
parts (![]() ) of the vector
) of the vector![]() , respectively. Let us denote the spectral transfer function for the ith subsystem by
, respectively. Let us denote the spectral transfer function for the ith subsystem by![]() , and by
, and by
![]()
its ![]() -matrix.
-matrix.
The contradiction of the SON conditions for the problem ![]() yields
yields
Theorem 1. The problem ![]() is locally proper at the s-process if for a certain admissible multiperiod
is locally proper at the s-process if for a certain admissible multiperiod ![]() and a critical direction
and a critical direction ![]() the inequality
the inequality
![]() (10)
(10)
holds, where ![]() is the second variation of
is the second variation of ![]() at
at ![]() taking the form
taking the form
![]()
or in the structural version
![]()
and ![]() are the submatrices of the matrix
are the submatrices of the matrix ![]() of the dimension
of the dimension ![]() with the upper left hand corner at
with the upper left hand corner at![]() .
.
Proof. Lemma 2 shows that the finite-dimensional optimal steady-state process satisfies the FON conditions with a nonzero Lagrange multiplier without regularity conditions. Lemma 3 shows that this process satisfies also the FON conditions of the optimal multiperiodic control problem regardless if it is local minimum or not. This means that such conditions do not allow to distinguish improving multiperiodic control processes. For this reason the attention is directed to the SON conditions, which take for multiharmonic control variations especially simple form connected with the generalized ![]() -test for single systems [11] . If the condition (10) is satisfied then the optimal steady-state process cannot be optimal for the multiperiodic control problem as violating its SON conditions. In a consequence an improving multiperiodic control process exists for the multiperiod exploited in (10). W
-test for single systems [11] . If the condition (10) is satisfied then the optimal steady-state process cannot be optimal for the multiperiodic control problem as violating its SON conditions. In a consequence an improving multiperiodic control process exists for the multiperiod exploited in (10). W
The discussed second order test has the following distinctive features: it concerns the different (possibly incommensurate) basic operation frequencies ![]() of the particular subsystems utilizing advantageously their dynamic properties; structural notation of the pi-form distinguishes the improving influence of the variations of the internal as well as the upper and lower boundary extended controls; even for boundary steady-state extended controls an arbitrary large number of harmonics
of the particular subsystems utilizing advantageously their dynamic properties; structural notation of the pi-form distinguishes the improving influence of the variations of the internal as well as the upper and lower boundary extended controls; even for boundary steady-state extended controls an arbitrary large number of harmonics ![]() is applicable in the second order variation, which may be useful for highly nonlinear complex systems; the maximization in the condition (10) is equivalent to the linear programming problem solvable in finite number of iterations by the simplex algorithm avoiding the verification of the regularity conditions for the
is applicable in the second order variation, which may be useful for highly nonlinear complex systems; the maximization in the condition (10) is equivalent to the linear programming problem solvable in finite number of iterations by the simplex algorithm avoiding the verification of the regularity conditions for the ![]() -process in the problem
-process in the problem![]() . On the other hand if the mentioned regularity condition can be verified by the MFCQ or the LICQ regularity condition then a normal multiplier
. On the other hand if the mentioned regularity condition can be verified by the MFCQ or the LICQ regularity condition then a normal multiplier ![]() is applicable in the second order test.
is applicable in the second order test.
4. Example
Let two continuously stirred tank reactors be coupled by the inventory interactions. In each of them the parallel chemical reactions ![]() take place, where
take place, where ![]() is the substrate of the ith reactor,
is the substrate of the ith reactor, ![]() is its desired product, and
is its desired product, and ![]() is its by-product
is its by-product![]() . The ith reactor is
. The ith reactor is ![]() -periodically operated,
-periodically operated, ![]() are its concentrations of
are its concentrations of![]() , respectively, and
, respectively, and ![]() is its state,
is its state, ![]() is its input concentration control,
is its input concentration control, ![]() is its input intensity control, and
is its input intensity control, and ![]() is its inventory interaction transferring the by-product of the cooperating subsystem as the catalyst of its reactions, and
is its inventory interaction transferring the by-product of the cooperating subsystem as the catalyst of its reactions, and ![]() is its extended control. Consider the following optimal control problem for the discussed system: minimize the objective function
is its extended control. Consider the following optimal control problem for the discussed system: minimize the objective function
![]()
being a scalar function of the averaged outputs
![]()
with
![]()
and subject for ![]() to the local constraints
to the local constraints
![]()
![]()
![]()
![]()
![]()
and to the interaction constraints
![]()
Thus![]() . The objective function is equivalent to the maximization of the summary gain from the useful products of both reactors. The cost of the interactions is included. We assume the parameters
. The objective function is equivalent to the maximization of the summary gain from the useful products of both reactors. The cost of the interactions is included. We assume the parameters![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . The optimal steady-state solution is obtained for the boundary input concentration controls and the internal other controls
. The optimal steady-state solution is obtained for the boundary input concentration controls and the internal other controls![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
The variation of the optimal steady state solution![]() ,
, ![]() ,
, ![]() moves the boundary input concentration controls to the interiority of their box sets, and satisfies all the constraints of the set of critical directions:
moves the boundary input concentration controls to the interiority of their box sets, and satisfies all the constraints of the set of critical directions:
![]()
![]()
The positive component of the second order test generated by the steady state variation ![]() does not disturb the multiperiodic control problem to be proper.
does not disturb the multiperiodic control problem to be proper.
The multifrequency second order test for the discussed complex system with the inventory interactions is shown on Figure 1 and Figure 2 for different number of harmonics.
The second order test obtained shows the diversified advantageous operation frequencies for particular subsystems ![]() and
and ![]() for the single harmonic and
for the single harmonic and ![]() and
and ![]() for the five harmonics. Thus the multiharmonic test may yield more exact information concerning the proper operation periods for particular subsystems.
for the five harmonics. Thus the multiharmonic test may yield more exact information concerning the proper operation periods for particular subsystems.
![]()
Figure 1. The single harmonic second order test for the complex system with the inventory interactions.
![]()
Figure 2. The five harmonics second order test for the complex system with the inventory interactions.
5. Conclusion
In this note, we formulated the optimal multiperiodic control problem for inventory constrained subsystems. It is aimed at the intensification of the productivity of complex processes. We proposed a multifrequency second-order test for complex multiperiodic systems including the boundary optimal steady-state process and an arbitrary large number of harmonics used to verify its improvement by the multiperiodic operation. We generalized the method of critical directions for single periodic systems [10] [11] to complex multiperiodic systems. We illustrated the approach proposed on the example of the multiperiodic optimization of a system of chemical reactors.
Acknowledgements
This work has been supported by the National Science Center under grant: 2012/07/B/ ST7/01216.