Reactive Transport Numerical Model for Durability of Geopolymer Materials ()
1. Introduction
Geopolymer is a sub-group of alkali-activated (calcium)-alumino-silicate binders sub- categorised by a criteria of low Ca content (below 5 - 10 mass%). They harden due to formation of 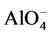 -SiO4 tetrahedral framework, where alkali or alkaline earth cations (Na+, K+, Ca2+), as well as H+ act as charge balancing species [1] [2] . Diffusive transport coupled with ion exchange reactions in geopolymer materials plays a crucial role in both the degradation process of building materials (e.g. mortar and concrete) [2] and the containing of hazardous wastes. Alkali ions such as sodium and potassium precursors readily leach out from the geopolymer material causing pH reduction and possible corrosion of reinforcing steel in concrete. The initial alkalinity of the pore solution of geopolymer pastes, determined directly after high pressure pore fluid expression [2] , and its leaching behavior has been investigated in literature [2] [3] . However, currently leaching is described as a pure diffusion process, disregarding the ion exchange reactions which include high amount of bound alkali to be available as a source in the pore solution that lowers the rate of its alkalinity drop during leaching process.
-SiO4 tetrahedral framework, where alkali or alkaline earth cations (Na+, K+, Ca2+), as well as H+ act as charge balancing species [1] [2] . Diffusive transport coupled with ion exchange reactions in geopolymer materials plays a crucial role in both the degradation process of building materials (e.g. mortar and concrete) [2] and the containing of hazardous wastes. Alkali ions such as sodium and potassium precursors readily leach out from the geopolymer material causing pH reduction and possible corrosion of reinforcing steel in concrete. The initial alkalinity of the pore solution of geopolymer pastes, determined directly after high pressure pore fluid expression [2] , and its leaching behavior has been investigated in literature [2] [3] . However, currently leaching is described as a pure diffusion process, disregarding the ion exchange reactions which include high amount of bound alkali to be available as a source in the pore solution that lowers the rate of its alkalinity drop during leaching process.
Modeling alkali leaching of geopolymer materials is challenging due to the multi- scale porous and multi-phase nature of their amorphous zeolite building matrix [1] [2] . The mechanisms of alkali loss and the equilibrium alkali concentration (ion exchange and solubility) are different for each of these phases, depending mainly on their silicium to aluminium ratio. Most common approaches to overcome these difficulties consist on either limiting the number of phases considered or using a continuous (smeared out) equilibrium formulation for bound solid alkali concentration as a function of its equilibrium solution concentration. The later (smeared out) approach is employed here.
In this paper a diffusive transport coupled with alkali equilibrium solid-liquid reactions is presented to take into account the additional capacity of the alkalies that are bound as charge balancing species within the 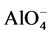 -SiO4 tetrahedral framework of the geopolymerisation (condensation) product. The modelling approach follows a Langmuir binding isotherm approach. An advanced numerical implementation employs Matlab’s built-in solvers “pdepe.m” and “ode15s.m” based on implicit Petrov-Galerkin method of lines (second-order accurate) for space discretization and an implicit time integration scheme that changes both the time step and the computing formula dynamically in order to minimize computational time for a desired accuracy. Simulations were compared against literature measurement data [2] .
-SiO4 tetrahedral framework of the geopolymerisation (condensation) product. The modelling approach follows a Langmuir binding isotherm approach. An advanced numerical implementation employs Matlab’s built-in solvers “pdepe.m” and “ode15s.m” based on implicit Petrov-Galerkin method of lines (second-order accurate) for space discretization and an implicit time integration scheme that changes both the time step and the computing formula dynamically in order to minimize computational time for a desired accuracy. Simulations were compared against literature measurement data [2] .
2. Mathematical Model
Alkali leaching in geopolymer materials is a coupled chemical reaction/diffusion phenomenon. Kinetics of transport-reaction processes in porous media are mostly described by a simplified continuum (homogenized) model Equation (1) where the actual evolution of the pore morphology, chemical activity, reaction rate, convection, electrical coupling and precipitation effects are neglected.
 (1)
(1)
where, Deff is the effective diffusion coefficient (m2・s−1), c is the concentration of Na+ in the pore solution (mol・m−3), r is reaction term (mol・m−3・s−1), p is the porosity, x is depth of the paste sample and t is duration of a leaching process. The first term on the right- hand side of Equation (1) stands for the diffusion process of the alkali in the liquid phase, which is assumed to be governed by Fick’s law. The second term accounts for the dissolution process, which leads to a source of alkali in the liquid phase. The kinetics of the dissolution reaction is governed by a diffusion process, because the diffusion rates are much slower than those of the chemical reactions. In this case the alkali concentration in the solid phase Cb(x,t) is calculated from its equilibrium relationship with the alkali concentration in the solution.
2.1. Alkali Binding
Alkali binding of Na+ within the Na-geopolymer paste can be described by following ion exchange reaction:
 (2)
(2)
where {Si-O-Al-O}- refers to the negatively charged exchange site occupied by the charge compensating cations Na+, K+ or H+. In a first approximation when neglecting competition with other cations like H+ and K+, an equilibrium constant or selectivity coefficient, Keq (m3/mol), just for Na+ binding can be written as:
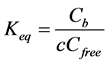 (3)
(3)
where Cfree is concentration of potential sites for sorption of Na+; Cb is concentration of Na+ occupied sites bound as {Si-O-Al-O}-Na, and c is concentration of Na+ in the pore solution. In this paper, as a first approach an ideal case is assumed where thermodynamic (TD) activities are equal to concentrations. This is reasonable as the calibrated Langmuir binding parameters obtained empirically in this paper account both for the non-ideality and the smeared out approach. However, when using a more advanced TD approach, considering the fundamental multi-component solid and solution speciation equilibria, should generally be based on real activities in order to have a good TD model-database consistency.
Solid concentrations, Cfree and Cb are quantified here in units of mol/kg of solid, while solute concentration c is in units of mol/m3 of pore solution. Concentration of free sites available for sorption of Na+ can be expressed as:
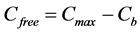 (4)
(4)
i.e. the number of available free sites for Na+ sorption is diminished by the number of occupied sites by Na+. Combining Equations (3) and (4) gives:
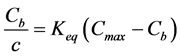 (5)
(5)
which by solving for Cb yields a Langmuir binding isotherm:
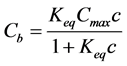 (6)
(6)
Bound alkalies provide the geopolymer paste with a large reservoir of exchangeable (soluble) alkali.
2.2. Diffusion Reaction Model
The mathematical model adopted is based on the diffusion-reaction model given as Equation (1). Reaction term (r) can be considered in two ways depending on a relative rates between binding and transport. If a binding rate is faster than transport, an equilibrium isotherm is assured. The reaction rate is then calculated as:
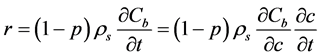 (7)
(7)
where ρs is density of the solid part of geopolymer paste and the required differential term is obtained by differentiating the Langmuir binding isotherm Equation (6) with respect to c:
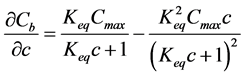 (8)
(8)
Solid concentrations Cb, Cmax are in units of mol/kg of solid, and solute concentration is in mol/m3 of pore solution. The total concentration of Na in mol/m3 of material can be defined as a sum of free and bound chlorides, where the units are transformed by considering concrete porosity (p) and density of the solids (ρs):
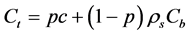 (9)
(9)
By writing the Fick’s law for total concentration, and inserting Equation (9) the accumulation term would split to two differential terms with respect to time, while the diffusive flux can be assigned only to soluble (free moving) ions, would derive Equation (1) where reaction term is represented by Equation (3).
To reduce the number of parameters to be determined simultaneously with the inverse analysis, it is proposed here to use experimental data on the binding isotherm for the case of material’s initial condition (leaching time t = 0). Keq can be expressed as a function of Cmax by combining the Equation (3) and Equation (4):
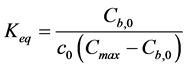 (10)
(10)
From the experimental results of the pore extraction analysis one can obtain the concentration of Na+, while the corresponding equilibrated bound concentration can be calculated from the total concentration of Na in the system (Ct), according to:
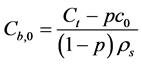 (11)
(11)
3. Numerical Implementation
The Matlab’s built-in non-linear solver “pdepe.m” based on Petrov-Galerkin method of lines is used [4] . The method of lines proceeds by first discretizing the spatial derivatives only and leaving the time variable continuous. This leads to a system of ordinary differential equations to which a numerical method for initial value ordinary equations can be applied. The partial differential equation was converted to ordinary differential equations using a second-order spatial discretization based on a fixed set of user defined nodes [5] [6] . The time integration is done with the Matlab’s built-in solver “ode15s.m” for solving stiff system of differential algebraic equations. This routine changes both the time step and the computing formula dynamically in order to minimize computational time for a desired accuracy [6] . The second-order algorithm “pdepe.m” and the variable time step integration “ode15s” will provide a good convergence rate and is robust enough to handle non-linearities and the couplings of the equations. Furthermore, the usage of Matlab’s built-in solver provides a convenient platform for easy and reliable implementation of future improvements such as the more detailed description of the chemical interaction of the diffusing ions with the solid phase, time and space dependency of the diffusion parameters, and the pore water convection movement, e.g. capillary suction effect.
4. Simulation and Calibration
Experimental data on sodium leaching from geopolymer paste are taken from [2] . Geopolymer pastes were made by activation of class F fly ash by a blended solution of sodium silicate and sodium hydroxide (7% Na2O 7% SiO2 by mass of binder). Density of fly ash as well as of a reacted solid geopolymer part was assumed to be 2600 kg/m3. Water to binder ratio was w/b = 0.325 and achieved porosity was p = 0.305. Samples were cured in sealed moulds for 48 h at 65˚C, then demoulded and aged at 23˚C for 90 days before tested for sodium leaching. One-dimensional leaching test involved immersion of partly coated geopolymer discs in 600 mL of stirred deionised water, maintained at 23˚C. The eluted cation concentration was measured over time by ICP-OES. Further experimental details are given in [2] . From their mix design the total amount of Na2O was 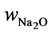 = 0.07 by mass of binder. One can transform this value to total concentration, Ct = 3182 mol/m3 of geopolymer material by:
= 0.07 by mass of binder. One can transform this value to total concentration, Ct = 3182 mol/m3 of geopolymer material by:
 (12)
(12)
where 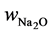 is mass ratio of Na2O per mass of binder,
is mass ratio of Na2O per mass of binder, 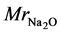 is molar mass of Na2O (61.98 g・mol−1), factor 2 comes from the fact that there are 2 moles of Na in 1 mol of Na2O, and mbinder is amount of binder, 1409 × 103 g per m3 of geopolymer material which was recalculated from binder density (for fly ash assumed here to be ρbinder = 2600 kg m−3) and water to powder ratio used for the mix design (w/b = 0.325 [2] ):
is molar mass of Na2O (61.98 g・mol−1), factor 2 comes from the fact that there are 2 moles of Na in 1 mol of Na2O, and mbinder is amount of binder, 1409 × 103 g per m3 of geopolymer material which was recalculated from binder density (for fly ash assumed here to be ρbinder = 2600 kg m−3) and water to powder ratio used for the mix design (w/b = 0.325 [2] ):
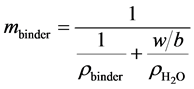 (13)
(13)
From the experimental results of the pore extraction analysis the concentration of Na+ is c0 = 612 mol/m3 and in this paper, it is proposed to obtain the corresponding equilibrated bound concentration from Equation (11), which yields Cb,0 to be 1.6580 mol/kg of geopolymer solids.
Introducing the initial binding isotherm experimental point for geopolymer material at leaching time t = 0 we can express Keq as a function of Cmax, according to Equation (10). Inserting the known c value (c = 612 mol/m3 of pore solution) measured by pore fluid extraction and the bound Na content (Cb = 1.6580 mol/kg of solids), the functional dependency between Langmuir parameters Keq and Cmax is then defined as:
![]() (14)
(14)
Levenberg-Marquardt inverse analysis was performed to estimate Def and Cmax parameters by minimising the sum of squared residuals between modelled and experimental leaching results. Within the model the Keq is obtained from Equation (14).
5. Results
Comparison of modelled and experimental results is given in Figure 1. For a diffusion model (dotted curve) the initial amount of Na measured in the expressed pore solution was not enough to account for the amount of Na leached from the paste. This results in significant underestimation of the leached Na amount for times after around t0.5 = 400 s0.5, because no release of bound alkali is made possible within the plain diffusion model. After that time, the model asymptotically approaches to a constant steady state value of the system. However, introducing the reaction (equilibrium) term for release of bound alkali enables to describe the experimental observations. Levenberg-Marquardt inverse analysis (fitted model) obtained by minimising the sum of squared residuals yielded following estimates: Def = 3.95 × 10−11 m2/s; Cmax = 1.663 mol/kg; Keq = 0.5764 m3・mol−1. The value obtained by fitting oversimplified diffusion model gave 22% lower estimate (Def = 4.8 × 10−11 m2/s [2] ). More importantly the capacity to release bound alkali is discussed next. Figure 2 depicts modelled Na profile concentration (in same units of
![]()
Figure 1. Comparison of modelled and experimental results [2] . Levenberg-Mar- quardt inverse analysis (fitted model) obtained by minimising the sum of squared residuals resulted in estimates for Def = 3.95 × 10−11 m2/s; Cmax = 1.663 mol/kg; Keq = 0.5764 m3・mol−1.
![]()
Figure 2. Modelled Na profile concentration across sample thickness for leaching time t0.5 = 655 s0.5: dashed curve for total Na showing huge values on left ordinate compared to solid curve for relatively low amount of free Na on right ordinate (same units of mol/m3 of geopolymer paste).
mol/m3 of geopolymer paste) after a leaching time t0.5 = 655 s0.5. The dashed curve represents total Na values on left ordinate and solid curve represents free Na amount on right ordinate. The huge difference between the two curves emphasises the importance for introducing the ion-exchange equilibrium reactions in modelling of alkali leaching process from geopolymer materials.
There are two extreme external (boundary) condition scenarios on which geopolymer material can be exposed to: 1) rapid leaching of the pore solution from the material, e.g. due to external flow of water or 2) acid attack that neutralises the pore solution. In both cases the drop in alkali concentration of the pore solution (and thus its pH) is very sudden when there is no source of the dissolved alkalies from the solids. Dissolution of alkalies by ion exchange mechanism with protons allows for a more gradual drop in pH of the pore solution, as compared to a sudden drop when considering only diffusion transport mechanism with no release of bound alkalis.
The rate of drop in alkali concentration of the pore solution (and thus its pH) is then governed by the rate of the dissolution (Equations (7) and (8)), which is obtained by differentiating the Langmuir binding isotherm Equation (6) with respect to c. Initially, the drop in pH is high due to low ion exchange capacity (Figure 3): represented by a right end point in Langmuir curve where a large drop in free alkalies gives negligible amount (rate) of dissolved alkalies. The dissolution rate starts to be significant only when concentrations of the free Na+ are below around 25 mol/m3 of pore solution (Figure 3). Below this threshold point, the binding sensitivity (i.e. its rate) is now reversed: a small drop in free Na+ concentration is accompanied by a high amount of dissolved alkalies. This threshold corresponds to a pH of 12.4 which is very close to
![]()
Figure 3. Langmuir isotherm (Equation (6); Cmax = 1.663 mol/kg; Keq = 0.5764 m3・mol−1) obtained by the inverse analysis. For better visibility logarithmic scale was used across abscissa.
the value of saturated Ca(OH)2 solution of pH = 12.5.
The degree of Na+ binding selectivity among various kinds of zeolite structures, and thus also geopolymers, varies significantly depending on the prevailing factors of their structural frameworks [2] [7] . Various geopolymers have different semi-crystal structures arising from variations in composition, distribution and ordering of ![]() -SiO4 tetrahedral units in linkages of their global structural (Al-O-Si-) framework [1] [7] . Primarily, variability in Si/Al ratio results in differences in the location, amount and distribution of negative charge density in the structural frameworks, cages or pores of different diameters, nature or absence of hydration water or other ligands and presence and position of charge compensating cations.
-SiO4 tetrahedral units in linkages of their global structural (Al-O-Si-) framework [1] [7] . Primarily, variability in Si/Al ratio results in differences in the location, amount and distribution of negative charge density in the structural frameworks, cages or pores of different diameters, nature or absence of hydration water or other ligands and presence and position of charge compensating cations.
6. Conclusions
Plain diffusion model is inappropriate to describe the leaching of alkalies from geopolymer materials. For longer leaching times the model falsely starts to asymptotically approach a steady state condition with a significant underestimation of both the remaining alkali amount in pore solution as well as the amount leached into the environment. The newly proposed transport model is coupled to the reaction (equilibrium) term describing a release of bound alkalies and enables accurate predictions of the experimental observations. Bound alkalies provide the geopolymer paste with a large reservoir of exchangeable (soluble) alkali. The calculated huge difference between the simulated total and free alkali concentrations emphasises the importance for introducing the ion-exchange equilibrium reactions in modelling of alkali leaching process from geopolymer materials. Such a reservoir of potentially dissolvable alkalies allows for a more gradual drop in pH of the pore solution, as compared to a sudden drop when considering only diffusion transport mechanism with no release of bound alkalies. The bounded alkali concentration in the solid phase is calculated from Langmuir equilibrium relationship with the alkali concentration in the solution.
Levenberg-Marquardt inverse analysis was performed to estimate Def and Cmax (one of the Langmuir) parameters by minimising the sum of squared residuals between modelled and experimental leaching results. To reduce the number of parameters to be determined simultaneously with the inverse analysis, it is proposed to use experimental data on the binding isotherm for the case of material’s initial condition. From the pore extraction experimental analysis one can obtain the free concentration of alkali initially available in pore solution, while the corresponding equilibrated bound concentration is calculated from the total concentration of alkali in the system, which is known from mix design.
The proposed model for alkali leaching that accounts for ion-exchange solid-liquid equilibrium presents a more reliable way to obtain long term durability predictions of geopolymer materials.