Equilibrium Positions of a Cable-Connected Satellites System under Several Influences ()
Received 19 May 2016; accepted 4 September 2016; published 8 September 2016

1. Introduction
We study the equilibrium positions of the motion of a system of two cable-connected artificial satellites under the influence of solar radiation pressure, earth’s oblateness, shadow of the earth and air resistance. The influence of the above mentioned perturbations on the system has been studied singly and by a combination of any two or three of them by various workers, but never conjointly all at a time. Therefore, these could not give a real picture of motion of the system. This fact has initiated the present research work. The case of circular orbit of the centre of mass of the system is discussed. Shadow of the earth is taken to be cylindrical and the system is allowed to pass through the shadow beam. The satellites are connected by a light, flexible, inextensible and non-conducting cable. The satellites are taken as material particles. Since masses of the satellites are small and distances between the satellites and other celestial bodies are very large, the gravitational forces of attraction between the satellites and other celestial bodies including the sun have been neglected.
The present work is an attempt towards the generalization of work done by Beletsky and Novikova [1] and Beletsky and Novoorebelskii [2] . They studied the motion of a system of two satellites connected by a light, flexible and inextensible string in the central gravitational field of force relative to its centre of mass. This study assumed that the two satellites are moving in the plane of the centre of mass. Das et al. [3] studied the effect of magnetic force on the motion of a system of two cable-connected satellites in orbit. Kumar and Bhattacharya [4] studied the stability of equilibrium positions of two cable-connected satellites under the influence of solar radiation pressure, earth’s oblateness and earth’s magnetic field. Kumar et al. [5] obtained the equations of motion of a system of two cable-connected artificial satellites under the influence of solar radiation pressure, earth’s oblateness and shadow of the earth. Singh and Demin [6] and Singh [7] investigated the problem in two and three dimensional cases.
2. Equations of Motion and Jacobian Integral of the System
We write the equations of motion of one of the satellites when the centre of mass moves along Keplarian elliptical orbit in Nechvile’s co-ordinate system [8] as Prasad and Kumar [9] .
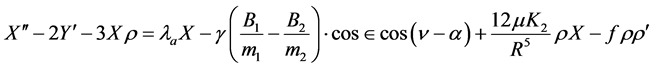
And
 (2.1)
(2.1)
With the condition of constraint
 (2.2)
(2.2)
Also,
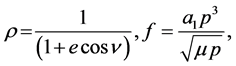

 (2.3)
(2.3)
m1 and m2 are masses of the two satellites. B1 and B2 are the absolute values of the forces due to the direct solar pressure on m1 and m2 respectively and are small. p is the focal parameter. m is the product of mass of the earth and gravitational constant. l is undermined Lagrange’s multiplier. 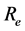 is equatorial radius of the earth.
is equatorial radius of the earth. 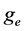 is the force of gravity. W is angular velocity of the earth’s rotation. aR is the earth’s oblateness.
is the force of gravity. W is angular velocity of the earth’s rotation. aR is the earth’s oblateness. 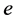 is ecentricity of the orbit of the centre of mass. v is the true anomaly of the centre of mass of the system.
is ecentricity of the orbit of the centre of mass. v is the true anomaly of the centre of mass of the system. 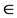 is inclination of the oscillatory plane of the masses m1 and m2 with the orbital plane of the centre of mass of the system. a is the inclination of the ray. γ is a shadow function which depends on the illumination of the system of satellites by the sun rays. If γ is equal to zero, then the system is affected by the shadow of the earth. If γ is equal to one, then the system is not within the said shadow.
is inclination of the oscillatory plane of the masses m1 and m2 with the orbital plane of the centre of mass of the system. a is the inclination of the ray. γ is a shadow function which depends on the illumination of the system of satellites by the sun rays. If γ is equal to zero, then the system is affected by the shadow of the earth. If γ is equal to one, then the system is not within the said shadow. 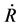 is the first order time derivative of R. R is the modulus of position vector of the centre of mass of the system. c1 and c2 are the Ballistic coefficients.
is the first order time derivative of R. R is the modulus of position vector of the centre of mass of the system. c1 and c2 are the Ballistic coefficients.  is the average density of the atmosphere. Prime denotes differentiation with respect to v.
is the average density of the atmosphere. Prime denotes differentiation with respect to v.
If motion of one of the satellites m1 be determined with the help of equations (2.1), motion of the other satellite of mass m2 can be determined by Prasad and Kumar [9] .
 (2.4)
(2.4)
where,  is the radius vector in the centre of mass System.
is the radius vector in the centre of mass System.
In the case of circular orbit, we put ,
, ![]() and
and ![]() in equations (2.1) and write
in equations (2.1) and write
![]()
And
![]() (2.5)
(2.5)
With the condition of constraint
![]() (2.6)
(2.6)
In the case of loose string, we see that![]() ,
, ![]() and m1 moves inside the circle
and m1 moves inside the circle
![]() ; whence
; whence ![]() (2.7)
(2.7)
The system of two satellites is allowed to pass through the shadow beam during its motion. Let us assume that ![]() is the angle between the axis of the cylindrical shadow beam and the line joining the centre of the earth and the end point of the orbit of the centre of mass within the earth’s shadow, considering the positive direction towards the motion of the system. The system starts to be influenced by the solar pressure when it makes an angle
is the angle between the axis of the cylindrical shadow beam and the line joining the centre of the earth and the end point of the orbit of the centre of mass within the earth’s shadow, considering the positive direction towards the motion of the system. The system starts to be influenced by the solar pressure when it makes an angle ![]() with the axis of the shadow beam and remains under the influence of solar pressure till it makes an angle
with the axis of the shadow beam and remains under the influence of solar pressure till it makes an angle![]() with the axis of the cylindrical shadow beam. Thereafter, the system will enter the shadow beam and the effect of solar pressure will come to an end.
with the axis of the cylindrical shadow beam. Thereafter, the system will enter the shadow beam and the effect of solar pressure will come to an end.
Next, the small secular and long periodic effects of the solar pressure together with the effects of the earth’s shadow on the system may be analysed by averaging the periodic terms in (2.5) with respect to ![]() from
from ![]() to
to ![]() for a period when the system is under the influence of the sun rays directly i.e.
for a period when the system is under the influence of the sun rays directly i.e. ![]() and from
and from ![]() to
to ![]() for a period when the system passes through the shadow beam i.e.
for a period when the system passes through the shadow beam i.e.![]() .
.
Thus after averaging the periodic terms of (2.5) we write the equations (2.5) as
![]()
And
![]() (2.8)
(2.8)
For the case of loose string, we use ![]() and write the above equations (2.8) as
and write the above equations (2.8) as
![]()
And
![]() (2.9)
(2.9)
These equations do not contain the time explicity. Therefore, Jacobian integral of the motion exists.
Multiplying the first and second equations of (2.9) by X' and Y' respectively, adding them and then integrating the final equation, we get the Jacobian integral in the form
![]() (2.10)
(2.10)
The surface of zero velocity can be obtained in the form
![]() (2.11)
(2.11)
![]() constant of Integration called Jacobian constant.
constant of Integration called Jacobian constant.
We, therefore, conclude that satellite ![]() moves inside the boundary of different curves of zero velocity, represented by (2.11) for different values of Jacobian constant
moves inside the boundary of different curves of zero velocity, represented by (2.11) for different values of Jacobian constant![]() .
.
3. Equilibrium Solution of the Problem
We have obtained a set of equations (2.9) for motion of the system in the rotating frame of reference. It is assumed that the system is moving with the effective constraint and the connecting cable of the two satellites always remains tight.
The equilibrium positions of motion of the system are given by the constant values of the co-ordinates in the rotating frame of reference. Let us take
![]() and
and ![]() (3.1)
(3.1)
![]() and
and ![]() are constant, give the equilibrium positions. Therefore, we get
are constant, give the equilibrium positions. Therefore, we get
![]() ;
; ![]()
![]() ;
;![]() (3.2)
(3.2)
Putting (3.2) in the set of equations (2.9), we get
![]()
And
![]() (3.3)
(3.3)
Actually it is very difficult to obtain the solution of (3.3). Hence, we are compelled to make our approaches with certain limitations. In addition to this, we are interested only in the case of the maximum effect of the earth’s shadow on motion of the system.
In the further investigation, we put ![]() and
and ![]() as because
as because ![]() or
or ![]() cannot be zero. Clearly equations (3.3) become
cannot be zero. Clearly equations (3.3) become
![]()
And
![]() (3.4)
(3.4)
All the two equations of (3.4) are independent of each other.
With the help of the two equations of (3.4), we get the equilibrium position as
![]() (3.5)
(3.5)
4. Conclusion
The equilibrium position has wide applications in solving problems of stability of a cable-connected satellites system in orbit. It will also state whether the motion of the system is continuous or not. We also write Jacobian integral of motion of the system. The work may be further modified, if wobbling and nutation of the orbit of the system are taken into account.
Acknowledgements
We acknowledge the support of Centre of Fundamental Research in Space Dynamics and Celestial Mechanics (CFRSC), Delhi. We are also thankful to Prof. R.K. Sharma from Thiruvanathapuram for his encouragement and support.
NOTES
![]()
*Corresponding author.