On Quantitative Approach to Parametric Identifiability of Dual HIV-Parasitoid Infectivity Model ()

Subject Areas: Mathematical Analysis, Numerical Mathematics, Operational Research, Ordinary Differential Equation

1. Introduction
The idea to continuously research into modalities of best informed approach towards tackling the seeming insurmountable deadly infection, globally known as human immunodeficiency virus―HIV, and its associated infectivity is primordial by the incurable status of the disease. Suppressitivity and preventability of HIV infection has become the dwelling options by which respite can be afforded by victims of this scourging infection. Achieving the above succor requires the understanding of the virus dynamics and the methodological application of affordable chemotherapy treatment [1] . Among the epidemiological approaches to the above, the mechanistic approach entails the identifiability and evaluation of the parameters with which an investigation is been conducted.
Based on the above premise, the present study proposes and by extension of earlier study [2] , couples with the model [3] , the formulation of a quantitative approach to parametric identifiability of dual HIV-parasitoid infectivity. The model is mechanically aimed at accounting for a novel differential 5-dimensional algebraic identifiability of parameters for dual HIV infectivity, as against most popular 3-D dynamic model for a single HIV infection [3] - [5] and 4-D dynamic HIV/AIDS model by [6] . In this model, nonlinear ordinary differential equation is explored for the formulation of the model and analysis conducted via nonlinear algebraic identifiability following the introduction of the concept of identifiability function and its associated identifiability equation. The model is subjected to a single treatment factor―reverse transcriptase inhibitor (RTI), with the use of Runge- Kutter of order 4 in Mathcad surface for simulation outcome.
Therefore, the novelty of the present model is the application of identifiability approach on two variable infectious diseases as compared to [2] - [4] [6] and also as a novel dimension, the model accounts for twelve parameters from a 5-D dynamic differential system as compared to models [3] [4] , which accounted for six system parameters and [6] , for ten parameters from popular 3-D dynamic system. Furthermore, the edging factor of this present model is in its envisage ability to accommodate the seeming complexity of parametric variables arising from dual infectivity. Additionally, the study is aimed at putting our earlier study [2] , on a proper footing, following the fact that identifiability is a differential basic property, which aids in the determination of whether parameters of a model can be uniquely estimated based on available measured output when other methods fail. Ideally, identifiability is basically an open possibility in parameter identification through solving available algebraic equations based only on the initial values and the measured output variables [3] .
The concept of identifiability of nonlinear systems in mathematical modeling has been studied and applied in different contexts. The model [3] , studied parameter identifiability and estimation of HIV/AIDS dynamic models, using technique from engineering, as was deployed by [6] ; and the deterministic and stochastic models of AIDS epidemics and HIV infection with intervention [4] , to investigate the algebraic identifiability of popular 3-D HIV/AIDS dynamics. Analysis of the model showed that with only available measurement of the viral load, not all the six parameters could be identified. Rather, only four parameters with the product of two were identifiable. In the study by [6] , identifiability of nonlinear systems with application to HIV/AIDS models was used in the investigation of different concepts of nonlinear identifiability in the generic sense. The study was applied to identifiability properties of a four-dimensional HIV/AIDS model. Result provided the minimal number of measurement of the variables required for a complete determination of all parameters of the model. In our previous study [2] , on analysis of parameter estimation for treatment of pathogen-induced HIV infectivity in a 5-D dynamic model, it was observed that the 5-D model was not compatible with discretization optimal control strategy, due to the indistinguishable nature of uninfected and infected CD4+ T cells, which degenerated to large error derivatives. Other notable application of identifiability in dynamic system could be found in [7] , in nonlinear system, see [8] - [10] , in algebraic identifiability of various HIV/AIDS dynamics, refer [4] and in Differential Equation Modeling of HIV Viral Fitness Experiments, in [11] .
The scope of this study is subdivided into 5 main sections, of which the introductory aspect occupies Section 1. In Section 2, we introduce the subject under investigation-identifiability of HIV-pathogen induced dynamic model. Section 3 is devoted to the derivation of the model identifiability function, which allows the introduction of two techniques―method of higher-order derivative (MHOD) and the method of multiple time point (MMTP). The validation of the parameter identifiability model and discussion form Section 4, of the work. Lastly, Section 5 presents the concluding part and recommendation arising from the study.
2. Identifiability of HIV-Pathogen Induced Dynamic Model
The dual infectivity considered here, consists of two infectious variables (HI-viral load and parasitoid-pathogen). In attempt to formulate this present model, we shall revoke the following two vital studies. First, the model [2] had studied the optimization control model for the treatment of pathogenic-induced HIV infections. Developed in that study, was a 5-D dynamic model, which investigated estimation of parameters on the basis of maximizing healthy CD4+ T cell count. The study assumed that virus infected CD4+ T cells were imperatively difficult to estimate due to the indistinguishable nature of the uninfected cells from the infected cells, refer [2] for more assumptions. Furthermore, the studies [3] [4] [6] , had used popular 3D dynamics, in conducting a number of studies, using several models on parameter identifiability. These studies equally affirmed the difficulties in the measurement of both uninfected and infected CD4+ T cells.
In our present model, referencing [3] [4] [6] , we extend the model [2] by exploring the use of quantitative approach in the parametric identifiability of two infectious variables (viral load and parasitoid-pathogen), with single chemotherapy (RTI) as treatment factor. Unlike [2] , the present study assumes and adopts the fact that the only available measurements are those of the viral load and parasitoid-pathogen. From model [2] , for a population defined by ―the uninfected CD4+ T cells,
―the uninfected CD4+ T cells,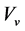 ―HIV virus (viral load),
―HIV virus (viral load),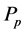 ―parasitoid-pathogen;
―parasitoid-pathogen; ―virus-infected CD4+ T cells and
―virus-infected CD4+ T cells and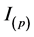 ―pathogen-infected CD4+ T cells , the biological and epidemiological model is governed by
―pathogen-infected CD4+ T cells , the biological and epidemiological model is governed by
 (2.1)
(2.1)
satisfying the conditions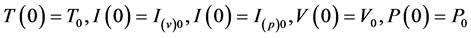 .
.
Let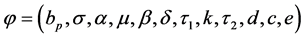 , denotes the system parameters with assumption that only the mea-
, denotes the system parameters with assumption that only the mea-
surements for V and P are available [3] [4] [6] . Therefore, by [12] , model (2.1), is said to be algebraically identifiable if there exist a time t, a positive integer z and a function:
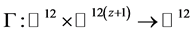
such that
 (2.2)
(2.2)
and
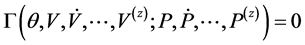 (2.3)
(2.3)
hold on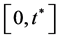 , where
, where 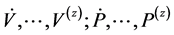 are the respective derivatives of V and P with respect to t. Equation (2.3) is called the “identifiability equation” and the function
are the respective derivatives of V and P with respect to t. Equation (2.3) is called the “identifiability equation” and the function![]() , is the identifiability function.
, is the identifiability function.
The realization of quantitative approach in identification model is in the ability to eliminate all unobserved state variables from the original system. The process of which involves computation of the higher order derivatives of the output variables. Therefore, form model (2.1); transforming the fourth and fifth equations by substituting the second and third equations, we derive the 2nd order derivatives as follows:
![]()
Substituting for ![]() and
and![]() ; and eliminating resulting
; and eliminating resulting ![]() and
and![]() , we have,
, we have,
![]() (2.4)
(2.4)
and
![]() (2.5)
(2.5)
From Equation (2.3), infection of CD4+ T cells by viruses are said to be simultaneous, therefore, summing Equations (2.4) and (2.5), we have,
![]() (2.6)
(2.6)
Taking the third derivative of Equation (2.6), we obtain
![]() (2.7)
(2.7)
Substituting the corresponding equations from model (2.1) and Equations (2.4) and (2.5), into Equation (2.7), we obtain:
![]()
Simplifying, we have
![]() (2.8)
(2.8)
Now, from Equations (2.4) and (2.5), we see that
![]() ;
;
![]()
implying that
![]() (i)
(i)
![]() (ii)
(ii)
From Equation (2.8), solving for ![]() and
and ![]() independently and substituting Equations (i) and (ii), respectively, we have
independently and substituting Equations (i) and (ii), respectively, we have
![]()
Or
![]()
Or
![]() (2.9)
(2.9)
Similarly,
![]() (2.10)
(2.10)
If we then substitute Equations (2.9) and (2.10) into (2.8), we derive
![]() (2.11)
(2.11)
Equation (2.11), is an equation that does not depend on the unobservable (latent) state variables ![]() and
and![]() . Furthermore, a close examination of the Equation (2.11), illuminate to the fact that only the parameters
. Furthermore, a close examination of the Equation (2.11), illuminate to the fact that only the parameters ![]() and
and ![]() each appear together as
each appear together as ![]() and
and ![]() respectively. This suggests that the pair is indistinguishable and only their product can be identified for variable measurement of viral load and parasitoid-pathogen.
respectively. This suggests that the pair is indistinguishable and only their product can be identified for variable measurement of viral load and parasitoid-pathogen.
Therefore, the parametric estimation of the model parameters, as a major breakthrough for the evaluation of impact of chemotherapy on dual HIV infectivity, ultimately requires the reparameterization of system parameters. Achieving this, we let
![]() .
.
Then, there exist a one-to-one mapping between
![]() and
and![]() .
.
If we denote the right-hand side of Equation (2.11) by![]() , then Equation (2.11) can be written as:
, then Equation (2.11) can be written as:
![]() (2.12)
(2.12)
The contribution of each of the parameters to the system can be explain from the partial derivative of Equation (2.12), with respect to each of the reparametized parameters, i.e.
![]() (2.13)
(2.13)
Thus, we are disposed with the option of identifying the twelve parameters, i.e. ![]() , implying the identification of the equivalent model parameters
, implying the identification of the equivalent model parameters![]() . Achieving this, twelve equations are essentially required. In reality, there exist two possibilities (or methods) with which to overcome the posed problem. We devote the next section to the construction and analyses of these identification functions.
. Achieving this, twelve equations are essentially required. In reality, there exist two possibilities (or methods) with which to overcome the posed problem. We devote the next section to the construction and analyses of these identification functions.
3. Derivation of Model Identification Function
We shall derive using Equations (2.11) and (2.12), the identification functions as solution of the system, based on the following two approaches―method of higher-order derivative (MHOD) and method of multiple time point (MMTP).
3.1. Method of Higher-Order Derivative (MHOD)
The construction and derivation of the identifiability of a 5-dimensional differential pathogenic induced HIV infection via method of higher-order derivative, is an extension of the method initiated by [3] , in a 3D-dynamic HIV model. The study essentially investigated the elimination of unobservable state variables from the original system.
In this present study, taking into account the above mentioned procedure, we construct the higher-order identifiable function for a 5D-basic model (2.1), as:
![]() .
.
Then, ipso facto
![]() ,
,
The identifiability of![]() , is visible and in accordance with the implicit function theorem [12] . It follows that,
, is visible and in accordance with the implicit function theorem [12] . It follows that,
![]() (2.14)
(2.14)
So we can essentially identify the twelve parameters of our model. The identifiability function, ![]() thus involves the 14th order derivatives of
thus involves the 14th order derivatives of![]() , which requires at least 15 measurements of
, which requires at least 15 measurements of![]() , to evaluate. Again, we are then confronted with a high dimensional parameter space, which becomes very complicated in it numerical calculation with complex rank to evaluate. We buttress the above submission setting an instance, the
, to evaluate. Again, we are then confronted with a high dimensional parameter space, which becomes very complicated in it numerical calculation with complex rank to evaluate. We buttress the above submission setting an instance, the
![]()
from [1] , where the rank of an element in the matrix was obtained as:
![]()
Then, it is difficult to evaluate the rank of such whole matrix of order 5 × 5. Thus, it is evidently much more difficult taking any element of a matrix with
![]() .
.
Overcoming this cancerous complexity in evaluation of such higher-order derivatives, we introduce to the model, an alternative method in constructing the desired identification function![]() , as presuppose by the next subsection.
, as presuppose by the next subsection.
3.2. Method of Multiple Time Point (MMTP)
Suppose we create the environment for which the quantities![]() , are at 12 distinct time points
, are at 12 distinct time points![]() . If we denote the values of
. If we denote the values of![]() , at
, at ![]() as
as ![]() for
for![]() , then, for
, then, for
![]() ,
,
we derive from Equations (2.11) and (2.12),
![]() (2.15)
(2.15)
If
![]()
then by the implicit function theorem, there is a unique solution of![]() , to Equation (2.15). Thus, in the assumption that
, to Equation (2.15). Thus, in the assumption that ![]() and recalling the derivatives (2.13), it is observed that the rank of
and recalling the derivatives (2.13), it is observed that the rank of ![]() algebraically coincide with the rank of
algebraically coincide with the rank of
![]() (2.16)
(2.16)
where,
![]()
So, we see that as much as![]() , we have
, we have![]() . Therefore, it becomes evidently clear that for every
. Therefore, it becomes evidently clear that for every ![]() computed at one time point, we needed at least, seven measurements of V and P. Then,
computed at one time point, we needed at least, seven measurements of V and P. Then,
in order to formulate the twelve identification equations from Equation (2.15), fifteen measurements of V and P are required. The case here, is that the model is locally identifiable, on the account that ∑, contain some unknown parameters. Therefore, the perceptive approach of MMTP is said to be consistent with that of MHOD. The outstanding positive side of MMTP when compared with MHOD, is the less computational intensity and much more compatible and implementable due to its ≤3, lower-order derivatives for V and P.
Furthermore, the matrix ∑, of Equation (2.16), cannot be ascertained as a full rank matrix by mere observability or first-hand algebraic operation. A known practical approach is the application of numerical simulation, which quantitatively computes the rank of ∑. We initiate this approach by first simulating the output variables of ![]() and
and ![]() at a sequence of time points from the basic model (2.1), using some fixed parameters. The higher-order derivatives of
at a sequence of time points from the basic model (2.1), using some fixed parameters. The higher-order derivatives of ![]() and
and ![]() can be evaluated using local polynomial or other smoothing methods based on the numerical evaluation of
can be evaluated using local polynomial or other smoothing methods based on the numerical evaluation of ![]() and
and![]() . This is followed by the calculation of the determinant of ∑, from Equation (2.16), to affirm the completeness of its rank status. To acclaim the completeness of the rank of ∑, it is necessary to repeat the calculation over a grid of parameter values. This method, though ad hoc in nature, is practically visible and useful when compared to the computationally tedious and expensive method of higher-order derivative of Equation (2.14).
. This is followed by the calculation of the determinant of ∑, from Equation (2.16), to affirm the completeness of its rank status. To acclaim the completeness of the rank of ∑, it is necessary to repeat the calculation over a grid of parameter values. This method, though ad hoc in nature, is practically visible and useful when compared to the computationally tedious and expensive method of higher-order derivative of Equation (2.14).
On the basis of the above, we provide as in Table 1, the summary of identifiability process in a 5D-dynamic model as compared with those of 3D-models by [3] [4] .
Now, for a dynamic system with unobservable state variables such as our 5D HIV-pathogen model, having unknown state variables, we avoid the use of the original Equation (2.1), in the evaluation of the unknown identifiable parameters. Here, we necessarily deploy the identifiability equations in obtaining the parameter esti-
![]()
Table 1. Algebraic identifiability of 5D and 3D HIV models.
mates. Achieving this, we revoke Equation (2.11), which is with only viral load and parasitoid-pathogen as observable variables to impress on the problem of model (2.1).
Therefore, we rewrite Equation (2.11) as:
![]() (2.17)
(2.17)
![]() (2.18)
(2.18)
![]() (2.19)
(2.19)
![]() (2.20)
(2.20)
implying that
![]() (2.12)
(2.12)
![]() .
.
Equation (2.21) is the desired equation, which is solvable if the initial values of the output variables (observables) V and P are known. That is, the identifiable parameters can be evaluated without the need for the unobservable state variables ![]() and
and![]() .
.
In real situation, we further simplify Equation (2.21), on the account that initial values of![]() , are not precisely known. In this case, if we let these variables assume zero values, then Equation (2.21) can be deduced to read:
, are not precisely known. In this case, if we let these variables assume zero values, then Equation (2.21) can be deduced to read:
![]() (2.22)
(2.22)
![]() .
.
Thus, we see that our basic model Equation (2.1), which contain both unknown (unobservable) state variables![]() and
and![]() ; and the observable state variables V and P, have been constructed and described only in terms of the available state variables. Therefore, Equation (2.22), competently lessen the burden of parameter identifiability, as simulation can be computed without loss of set goals. The validity of the model forms the next section of the work.
; and the observable state variables V and P, have been constructed and described only in terms of the available state variables. Therefore, Equation (2.22), competently lessen the burden of parameter identifiability, as simulation can be computed without loss of set goals. The validity of the model forms the next section of the work.
4. Validation of Identifiability Model and Discussion
In this section, following the administration of RTI treatment schedule, we validate the outcome of our quantitative analysis by the application of our constructed model Equation (2.22), in performing a number of numerical simulations with the aid of Runge-Kutter of order of precision 4, in a Mathcad surface. This is followed by a succinct discussion of the entire quantitative analysis and the outcome of computed illustrations.
4.1. Validation of Parameter Identifiability Model
In order to accomplish the desired task, we generate both our observable state variables and hypothetical initial parameter values base on previous HIV-Pathogen dynamic model by [8] . Invoking from that model (Table 2), we modify the initial state unobserved variables i.e. ![]() and
and![]() , while the observable state variables denoted by
, while the observable state variables denoted by![]() , are known. Here, the identifiability process shall involve step-wise variation of the parameters (zero variant), in order to estimate its identifiable impact respectively. Therefore, the derive simulation table for this present model is as seen in Table 2.
, are known. Here, the identifiability process shall involve step-wise variation of the parameters (zero variant), in order to estimate its identifiable impact respectively. Therefore, the derive simulation table for this present model is as seen in Table 2.
From Equation (2.22), the twelve parameter can be verified in the following six simulations and having a general representation with the seventh simulation.
Case 1: ![]() unknown (i.e.
unknown (i.e.![]() ). To be able to identify and estimate the impact of source of population birthrate on the system, we let the parameter take the zero value, keeping other parameter values as there were in Table 2, above. The computational simulation is as seen in Figures 1(a)-(c).
). To be able to identify and estimate the impact of source of population birthrate on the system, we let the parameter take the zero value, keeping other parameter values as there were in Table 2, above. The computational simulation is as seen in Figures 1(a)-(c).
From Figures 1(a)-(c), we observe that if source of infection rate is unknown but kept at zero when rate of replication is controlled at 50%, then after 30 months of chemotherapy schedule, viral load (1a), and decline in a diagonal trajectory to![]() . A skew declination is seen from parasitoid-pathogen (1b), to near zero
. A skew declination is seen from parasitoid-pathogen (1b), to near zero
![]() (a) (b) (c)
(a) (b) (c)
Figure 1. Identifiability of parameter![]() , for
, for ![]() (a) Simulation of viral load, bp = 0; (b) Simulation of p-pathogen, bp = 0; (c) Impact of bp = 0, on viruses.
(a) Simulation of viral load, bp = 0; (b) Simulation of p-pathogen, bp = 0; (c) Impact of bp = 0, on viruses.
![]()
Table 2. Variables and parameter values for model (2.22).
value after 24 months of chemotherapy. The overall impact of source of birth rate on dual infectivity (1c), indicates that infection decline to![]() .
.
Case 2: ![]() unknown (i.e.
unknown (i.e.![]() ). If only natural death rate of CD4+ T cells is at zero value, while rate of viruses replication are controlled at 50%, we simulate the system as represented in Figures 2(a)-(c).
). If only natural death rate of CD4+ T cells is at zero value, while rate of viruses replication are controlled at 50%, we simulate the system as represented in Figures 2(a)-(c).
Results from Figures 2(a)-(c), shows that, in 2(a), viral load exhibit inclinatory resilience at early onset of infection having its apex at 2 - 3 months, before declining to V = 0.141 ml, after 30 months of drug administration. For the parasitoid-pathogen as in 2(b), with zero natural death rate, infection decline rapidly and terminating after 24 months of chemotherapy treatment. Overall decline of viruses infected T-cells is put at Np = 0.143 ml.
Case 3: ![]() and
and ![]() unknown (i.e.
unknown (i.e.![]() ). If the rate at which CD4+ T cell becoming infected by both viruses are unchecked, such that
). If the rate at which CD4+ T cell becoming infected by both viruses are unchecked, such that![]() , with other parameters as in Table 2, then we simulate as seen in Figures 3(a)-(c).
, with other parameters as in Table 2, then we simulate as seen in Figures 3(a)-(c).
From Figures 3(a)-(c), we observe a diagonal trajectory decline of viral load with that of parasitoid pathogen slightly skew from 0.2 ml, to ![]() and
and![]() , respectively. The overall impact of these parameters on infection rate is computed at
, respectively. The overall impact of these parameters on infection rate is computed at![]() .
.
Case 4: ![]() and
and ![]() unknown (i.e.
unknown (i.e.![]() ). If the rate at which viral load and parasitoid pathogen attack and infect CD4+ T cell are unknown, such that there assume zero values, then infections are bound to decline following the application of chemotherapy treatment. The simulations of these parameters are as in Figure 4(a) and Figure 4(b).
). If the rate at which viral load and parasitoid pathogen attack and infect CD4+ T cell are unknown, such that there assume zero values, then infections are bound to decline following the application of chemotherapy treatment. The simulations of these parameters are as in Figure 4(a) and Figure 4(b).
From the above simulation, the non-continuity of rate of infection avail us with the identifiable impact of the parameters (![]() and
and![]() ). We observe gradual skew trajectory declination of both viral load (as in 4(a), to
). We observe gradual skew trajectory declination of both viral load (as in 4(a), to![]() ) and a corresponding rapid decline of parasitoid-pathogen (as in 4(b), to
) and a corresponding rapid decline of parasitoid-pathogen (as in 4(b), to![]() ), after a duration of 30 months of chemotherapy schedule. The decline in infection by both viruses for
), after a duration of 30 months of chemotherapy schedule. The decline in infection by both viruses for![]() , is computed to be
, is computed to be![]() , as represented in Figure 4(c).
, as represented in Figure 4(c).
![]() (a) (b) (c)
(a) (b) (c)
Figure 2. Identifiability of parameter![]() , for
, for ![]() (a) Simulation of viral load, μ = 0; (b) Simulation of p-pathogen, μ = 0; (c) Impact of μ = 0, on viruses.
(a) Simulation of viral load, μ = 0; (b) Simulation of p-pathogen, μ = 0; (c) Impact of μ = 0, on viruses.
![]() (a) (b) (c)
(a) (b) (c)
Figure 3. Identifiability of parameter β and δ, for ![]() (a) Simulation of viral load, β = 0; (b) Simulation of p-pathogen, δ = 0; (c) Impact of β = 0 = δ, on viruses.
(a) Simulation of viral load, β = 0; (b) Simulation of p-pathogen, δ = 0; (c) Impact of β = 0 = δ, on viruses.
![]() (a) (b) (c)
(a) (b) (c)
Figure 4. Identifiability of parameter σ and α, for ![]() (a) Simulation of viral load, σ = 0; (b) Simulation of p-pathogen, α = 0; (c) Impact of β = 0, δ = 0, on viruses.
(a) Simulation of viral load, σ = 0; (b) Simulation of p-pathogen, α = 0; (c) Impact of β = 0, δ = 0, on viruses.
Case 5: ![]() and
and ![]() unknown (i.e.
unknown (i.e.![]() ). For
). For ![]() as well as k and d having zero values, the corresponding simulations are as represented in Figures 5(a)-(c).
as well as k and d having zero values, the corresponding simulations are as represented in Figures 5(a)-(c).
From the Figures 5(a)-(c), the zero values of these identifiable parameters indicate that no death rate incurred by both infected CD4+ T cells and replications by viruses in infected cell were equally unknown. The implication is that infected population by both viruses remains stagnant throughout the 30 months period, de-
spite drug administration, i.e.![]() .
.
If only ![]() are zero, with
are zero, with ![]() and
and ![]() known as given in Table 2, (graph withheld for brevity), we see infection by viral load declining to
known as given in Table 2, (graph withheld for brevity), we see infection by viral load declining to![]() , as pathogen is completely near eradication after 24 months of treatment. The overall effect is simulated at
, as pathogen is completely near eradication after 24 months of treatment. The overall effect is simulated at![]() . On the other hand, if only
. On the other hand, if only ![]() are zero and
are zero and ![]() known to be as given in Table 2, (graph withheld for brevity), viral load and parasitoid-pathogen exhibit slight diagonal trajectory decline with
known to be as given in Table 2, (graph withheld for brevity), viral load and parasitoid-pathogen exhibit slight diagonal trajectory decline with ![]() and
and![]() . Resilience by overall infection is seen at
. Resilience by overall infection is seen at
![]() . Therefore, infection remains high due to constant replication with no loss of infected population.
. Therefore, infection remains high due to constant replication with no loss of infected population.
Case 6: ![]() and
and ![]() unknown (i.e.
unknown (i.e.![]() ). If k = 0, then
). If k = 0, then ![]() and for
and for![]() , implies that
, implies that![]() . The case is also true for
. The case is also true for![]() , when either
, when either ![]() or
or ![]() takes the value zero. The simulation having
takes the value zero. The simulation having![]() , is as seen in Figures 6(a)-(c).
, is as seen in Figures 6(a)-(c).
From the Figure 6(a)-(c), it observed that infections were slightly static with insignificant declination as observed in Figure 6(a) and Figure 6(b), where viral load and parasitoid-pathogen shows minute decline from ![]() respectively. The overall prevalence rate is obtained as
respectively. The overall prevalence rate is obtained as![]() , see Figure 6(c).
, see Figure 6(c).
Case 7: All parameters known. With the identifiability of the parameters and its impacts on viruses’ transmission and treatment schedule completely specified as in Table 2, we conduct an overall investigation as simulated in Figures 7(a)-(c).
We observe from Figure 7(a), that viral load exhibit initial slight toxicity at the first two months and declined to![]() , after 30 months of chemotherapy application. Under the same condition, parasitoid-pathogen drastically declined to near zero value after 24 months of drug administration. Infections reduced at an overall rate of
, after 30 months of chemotherapy application. Under the same condition, parasitoid-pathogen drastically declined to near zero value after 24 months of drug administration. Infections reduced at an overall rate of![]() , at the termination of treatment schedule.
, at the termination of treatment schedule.
4.2. Discussion
By extension, 5-dimensional algebraic identifiability model for parameter estimation of dual HIV parasitoid- pathogen was formulated with the introduction of novel identifiability function and its associated identification equation. The study deployed implicit function theorem from numerical methods in the derivation and analysis of two identification function methods. Twelve parameters of the model were established with ten independently identifiable, while only the product of the rest two pairs can be identified. Numerical computations of the model were conducted using existing known values of only observable state variables and compatible initial parameter
![]() (a) (b) (c)
(a) (b) (c)
Figure 5. Identifiability of parameter τ1, τ2, k and d, for ![]() (a) Simulation of viral load, τ1 + k = 0; (b) Simulation of p-pathogen, τ2 + d = 0; (c) Impact of τ1, τ2, k, d = 0, on viruses.
(a) Simulation of viral load, τ1 + k = 0; (b) Simulation of p-pathogen, τ2 + d = 0; (c) Impact of τ1, τ2, k, d = 0, on viruses.
![]() (a) (b) (c)
(a) (b) (c)
Figure 6. Identifiability of parameter kβ and dδ, for ![]() (a) Simulation of viral load, kβ = 0; (b) Simulation of p-pathogen, dδ = 0; (c) Impact of kβ = 0 = dδ, on viruses.
(a) Simulation of viral load, kβ = 0; (b) Simulation of p-pathogen, dδ = 0; (c) Impact of kβ = 0 = dδ, on viruses.
![]() (a) (b) (c)
(a) (b) (c)
Figure 7. Simulation with all parameters known ,for ![]() (a) Simulation of viral load with β, τ1, k, σ, c know; (b) Simulation of p-pathogen with δ, τ2, d, α, e know; (c) Impact of all parameters on viruses.
(a) Simulation of viral load with β, τ1, k, σ, c know; (b) Simulation of p-pathogen with δ, τ2, d, α, e know; (c) Impact of all parameters on viruses.
values from published works. Simulations were stratified into six main cases.
To be able to assimilate the results of the outcome of the identifiability computations, we consider the stratification of the parameter identifiability as follows: -identifiably predominant, if parameter is unknown (i.e. having zero value) and infection remained stagnant or characterized by insignificant decline of infection.; identified with weak predominant magnitude, if unknown, infection declined slightly with value not less than half the original value; identifiable with no predominant magnitude, if unknown, infection declined significantly with value near zero; and unidentifiable but having predominant impact, if unknown, infection exhibit insignificant decline.
In the aforementioned pattern, cases 1 and 2, exhibit identifiability properties with no predominant magnitude. On the other hand, cases 3 and 4, were characterized by identifiability status having weak predominant magnitude. Furthermore, in case 5, we experienced some special behavior. The sum of the parameters is identifiable with very strong predominant magnitude but as well, could exhibit the status of identifiability with no predominant magnitude when ![]() are unknown with known k and d. However, when
are unknown with known k and d. However, when ![]() are known with k and d unknown, case 5 exhibit predominant magnitude. Therefore, the binding here then lies with k and d.
are known with k and d unknown, case 5 exhibit predominant magnitude. Therefore, the binding here then lies with k and d.
The parameters of case 6, are independently unidentifiable but exhibits product identifiable predominant magnitude. This character affirmed the indistinguishable nature of uninfected CD4+ T cells from the infected T-cells. Finally, with all known identifiable parameters, their magnitude and impacts on the viruses and treatment dynamics were illustrated in case 7. Thus, it can be viewed that the key dominant parameters of the system lies in case 5 and 6, respectively.
5. Conclusion
In this paper, a novel differential 5-dimensional algebraic identifiability model for the estimation of parameters of dual HIV-parasitoid pathogen was formulated with the introduction of identifiability function, which led to the derivation of the model identifiability equations. Two observable state variables and twelve identifiable parameters constituted the derived model of the system. Analysis of the derived model was conducted via established novel techniques―MHOD and MMTP, with the later technique proven to be more practicable and less cumbersome in implementation. Validations of the outcome of model analyses were stratified into six strata, which simplified the trend of parameter identifiability predominant magnitude in a 5-dimensional dual HIV-pa- thogen dynamic model. Results show that cases 5 and 6, constituted by the rate of replication of viruses, rate at which viruses attacked the immune system and the rate at which the immune system became infected by viruses formed the core dominant identifiable parameters; when significantly controlled, eradication of dual infectivity can be achieved. Furthermore, the study was in agreement with existing results on the indistinguishable nature of uninfected CD4+ T cells from infected CD4+ T cells. Therefore, simulated outcome ascertained the theoretical analysis of the study, which can as well, be adapted conveniently to any nonlinear system of other related infectious diseases. Nonetheless, we acknowledge any further studies that may add novelty to the methodology and possible affirmation of the inputs of this work.
NOTES
![]()
*Corresponding author.