On-Line Scheduling for Jobs with Arbitrary Release Times on Parallel Related Uniform Machines

Xiayan Cheng¹, Rongheng Li², Yunxia Zhou³

¹Department of Mathematics, Hunan First Normal University, Changsha, China.
²Department of Mathematics, Key Laboratory of High Performance Computing and Stochastic Information Processing, Hunan Normal University, Changsha, China.
³Department of Computer, Hunan Normal University, Changsha, China.

DOI: 10.4236/iim.2016.84008                

Abstract

A parallel related uniform machine system consists of m machines with different processing speeds. The speed of any machine is independent on jobs. In this paper, we consider online scheduling for jobs with arbitrary release times on the parallel uniform machine system. The jobs appear over list in terms of order. An order includes the processing size and releasing time of a job. For this model, an algorithm with competitive ratio of 12 is addressed in this paper.

Keywords

Online Scheduling, Uniform Machine, Competitive Ratio, Approximation Algorithm

Received 18 February 2016; accepted 22 July 2016; published 25 July 2016

1. Introduction

For the online scheduling on a system of m uniform parallel machines, denoted by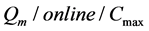, each machine has a speed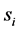, i.e., the time used for finishing a job with size p on 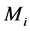is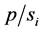. Without loss of generality, we assume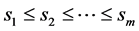. Cho and Sahni [1] are the first to consider the on-line scheduling problem on m uniform machines. They showed that the LS algorithm for 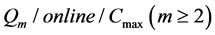has competitive ratio not greater than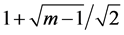. When 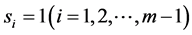and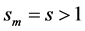, they

proved that the algorithm LS has a competitive ratio and the bound is achieved when.

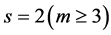For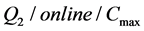, Epstein et al. [2] showed that LS has the competitive ratio and is an optimal online algorithm, where the speed ratio.

Cai and Yang [3] considered. Let and be two speed ratios. They showed that the algorithm LS is an optimal online algorithm when the speed ratios, where

and. Moreover, for the general speed ratios, they also presented an upper bound of the competitive ratio.

Aspnes et al. [4] are the first to try to design algorithms better than LS for. They presented a new algorithm that achieves the competitive ratio of 8 for the deterministic version, and 5.436 for its randomized variant. Later the previous competitive ratios are improved to 5.828 and 4.311, respectively, by Berman et al. [5] .

Li and Shi [6] proved that for LS is optimal when and and presented an online algorithm with a better competitive ratio than LS for. Besides, they also showed that the

bound could be improved when and. For and, Cheng et al. [7] proposed an algorithm with a competitive ratio not greater than 2.45.

A generalization of the Graham’s classical on-line scheduling problem on m identical machines was proposed by Li and Huang [8] - [10] . They describe the requests of all jobs in terms of order. For an order of the job, the scheduler is informed of a 2-tuple, where and represent the release time and the processing time of the job, respectively. The orders of request have no release time but appear on-line one by one at the very beginning time of the system. Whenever the request of an order is made, the scheduler has to assign a machine and a processing slot for it irrevocably without knowledge of any information of future job orders. In this on-line situation, the jobs’ release times are assumed to be arbitrary.

Our task is to allocate a sequence of jobs to the machines in an on-line fashion, while minimizing the maximum completion time of the machines. In the following of this paper, m parallel uniform machines which have speeds of respectively, are given. Let be any list of jobs, where job is given as order with the information of a release time and a processing size of.

The rest of the paper is organized as follows. In Section 2, some definitions are given. In Section 3, an algorithm U is addressed and its competitive ratio is analyzed.

2. Some Definitions

In this section we will give some definitions.

Definition 1. We have m parallel machines with speeds. Let be any list of jobs, where jobs arrives online one by one and each has a release time and a processing size of. Algorithm A is a heuristic algorithm. Let and be the makespan of algorithm A and the makespan of an optimal off-line algorithm respectively. We refer to

as the competitive ratio of algorithm A.

Definition 2. Suppose that is the current job to be scheduled with release time and size. We say that machine has an idle time interval for job, if there exists a time interval satisfying the following two conditions:

1) Machine is idle in interval and a job with release time is assigned on machine to start at time.

2).

It is obvious that if machine has an idle time interval for job, then we can assign to machine in the idle interval.

In the following we consider m parallel uniform machines with speeds and a job list with information for each job, where and represent its release time and size, respectively. For convenience, we assume that the sequence of machine speeds is non-decreasing, i.e.,

3. Algorithm U and Its Performance

Now we present the algorithm U by use of the notations given in the former section in the following:

Algorithm U:

Step 0. (*start the first phase*)

, ,.

Step 1. If there is a new job with release time and processing size given to the algorithm then go to Step 2. Otherwise stop.

Step 2. If there is a machine which has an idle time interval for job, then we assign to machine in the idle interval. Set and go to Step 1.

Step 3. Set. If then set, , Go to Step 1.

Step 4. (*start a new phase*)

Set, , and go to Step 3.

Now we begin to analyze the performance of algorithm U.

The following statement is obvious:

Lemma 1. Let be the stream of jobs scheduled in phase h and is the first job assigned in phase. Let be the largest load in an optimal schedule for job list. Then we have

Proof: If, let r be the fastest machine whose load does not exceed, i.e. . If there is no such machine, we set. If, then. It is

obvious that Hence we have

It means that can be assigned to the fastest machine in phase h. It is a contradiction to the fact that is the first job assigned in phase. Define, the set of machines with finishing time bigger than by the end of phase h. Since,. Denote by and the set of jobs assigned to machine by the on-line and the off-line algorithms, respectively. Since for any job the following inequalities hold

we get:

That means:

This implies that there exists a job () such that, i.e. there exists a job assigned by the on-line algorithm to a machine and assigned by the off-line algorithm to a slower machine.

By our assumptions, we have. Since, machine is at least as fast as machine, and thus. Since job was assigned before job and, we have

This implies

But this means that the on-line algorithm should have placed job on or a slower machine instead of, which is a contradiction. ¢

Theorem 2. Algorithm achieves a competitive ratio of 12.

Proof: Let denote the maximum load generated by jobs that were assigned during phase h; denote the last phase by. By the rules of our algorithm we have and

Hence the total height generated by the assignment is:

The claim of the theorem is trivially true if. For, phase h is started only if. In particular we have

Therefore we have

¢

4. Concluding Remarks

In this paper, we consider on-line scheduling for jobs with arbitrary release times on uniform machines. An algorithm with the competitive ratio of 12 is given. It should be pointed out that more detailed consideration should be taken in order to improve the competitive ratio.

Acknowledgements

The authors would like to express their thanks to the National Natural Science Foundation of China for financially supporting under Grant No. 11471110 and No. 61271264.

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Cho, Y. and Sahni, S. (1980) Bounds for List Schedules on Uniform Processors. SIAM Journal on Computing, 9, 91-103. http://dx.doi.org/10.1137/0209007
[2]	Epstein, L., Noga, J., Seiden, S.S., Sgall, J. and Woeginger, G.J. (2001) Randomized On-Line Scheduling on Two Uniform Machines. Journal of Scheduling, 4, 71-92. http://dx.doi.org/10.1002/jos.60
[3]	Cai, S.Y. and Yang, Q.F. (2012) Online Scheduling on Three Uniform Machines. Discrete Applied Mathematics, 160, 291-302. http://dx.doi.org/10.1016/j.dam.2011.10.001
[4]	Aspnes, J., Azar, Y., Fiat, A., Plotkin, S. and Waarts, O. (1997) On-Line Routing of Virtual Circuits with Applications to Load Balancing and Machine Scheduling. Journal of the ACM, 44, 486-504. http://dx.doi.org/10.1145/258128.258201
[5]	Berman, P., Charikar, M. and Karpinski, M. (2000) On-Line Load Balancing for Related Machines. Journal of Algorithms, 35, 108-121. http://dx.doi.org/10.1006/jagm.1999.1070
[6]	Li, R.H. and Shi, L.J. (1998) An On-Line Algorithm for Some Uniform Processor Scheduling. SIAM Journal on Computing, 27, 414-422. http://dx.doi.org/10.1137/S0097539799527969
[7]	Cheng, T.C.E., Ng, C.T. and Kotov, V. (2006) A New Algorithm for Online Uniform-Machine Scheduling to Minimize the Makespan. Information Processing Letters, 99, 102-105. http://dx.doi.org/10.1016/j.ipl.2006.02.012
[8]	Li, R.H., Cheng, X.Y. and Zhou, Y.X. (2014) On-Line Scheduling for Jobs with Non-Decreasing Release Times and Similar Lengths on Parallel Machines. Optimization: A Journal of Mathematical Programming and Operations Research, 63, 867-882. http://dx.doi.org/10.1080/02331934.2014.895902
[9]	Li, R.H. and Huang, H.C. (2004) On-Line Scheduling for Jobs with Arbitrary Release Times. Computing, 73, 79-97. http://dx.doi.org/10.1007/s00607-004-0067-1
[10]	Li, R.H. and Huang, H.C. (2007) Improved Algorithm for a Generalized On-Line Scheduling Problem on Identical Machines. European Journal of Operations Research, 176, 643-652. http://dx.doi.org/10.1016/j.ejor.2005.06.061