Stochastic Modelling of Vulnerability Life Cycle and Security Risk Evaluation ()
Received 20 June 2016; accepted 18 July 2016; published 21 July 2016

1. Introduction
In a recent study, “Cybersecurity: A Statistical Predictive Model for the Expected Path Length” (Journal of Information Security, 2016, 7, 112-128 [1] ), we introduced a method by which one can predict the Expected Path Length, the expected number of steps the attacker will take, starting from the initial state to achieve his target. In the present study, we propose a method using Markov chain to understand the Vulnerability Life Cycle and Security Risk behavior.
Any identified vulnerability [2] is hazardous to a security system and makes the system susceptible to be exploited until it is well patched. Therefore, we believe it is very important to know how to deal with a vulnerability behavior throughout its different stages. “Vulnerability Life Cycle” [3] would certainly help us to better understand the vulnerability and its behavior in a security system with respect to time. There are a number of ways to present the life cycle of a particular vulnerability. However, all these different introductions have several important stages in common. The level of the risk associated with different stages of vulnerability should be different indeed and need to be estimated.
However, measuring of such a “risk factor” [4] and obtaining a probabilistic estimate are certainly a challenge given the lack of data resources. If we have a method developed to measure the risk level associated with a particular vulnerability at a certain time or stage, it will help the users and organizations to act accordingly with well-defined priorities. Then the users and organizations can make sure adequate attention, resources and security intellects are employed to address such a risk and proper fixing steps are taken before it is exploited. One of the main objectives we have is to obtain a statistical model that can give us the probability of a vulnerability being exploited or patched at a given time. In this study, we use the well-known theory of Markov Chain Process to develop such a model.
2. Vulnerability and Vulnerability Life Cycle
In this section we will explain basic concept of Vulnerability, Vulnerability Life Cycle and related technical terms to make it easier to understand later sections.
Microsoft Security Response Center (MSRC) defines the term Vulnerability [2] - [6] as follows.
“A security vulnerability is a weakness in a product that could allow an attacker to compromise the integrity, availability, or confidentiality of that product”.
We understand that vulnerability could be derived by investigating the various weaknesses of an implemented security system. With a weakness in a custom design software, a vulnerability can come to effect in authentication protocols, software reliability and system process, Hardware management and Networking among others.
2.1. Common Vulnerability Scoring System (CVSS)
Common Vulnerability Scoring System (CVSS) [7] is a commonly used and freely available standard for assessing the magnitude of Information system Vulnerabilities. CVSS gives a score for each vulnerability scaling from 0 to 10 based on several factors. National Vulnerability Database (NVD) provides CVSS score and updates continuously with new vulnerabilities are found. CVSS score is calculated using three main matrices named, Base Matric, Temporal Metric and Environmental Metric. However, NVD data base provides us with the Base Metric Scores for the Vulnerability only because the Temporal and Environmental Scores are varied on other factors related to organization that uses the computer system. The Base score for more than 75,000 different vulnerabilities are calculated using 6 different Matrices. It is managed by the Forum of Incident Response and Security Teams (FIRST). CVSS establishes a standard measure of how much concern a vulnerability warrants, compared to other vulnerabilities, so efforts can be prioritized. The scores range from 0 to 10. Vulnerabilities with a base score in the range of 7.0 - 10.0 are considered “High”. Those in the ranges of 4.0 - 6.9, and 0 - 3.9 are considered as “Medium” and “Low” respectively.
2.2. Stages of Vulnerability Life Cycle
The Life Cycle of a Vulnerability [2] - [4] can be introduced with different stages that a vulnerability passes through. We shall discuss specific stages that are commonly identified in a given situation. Commonly identified stages are involved with the events such as the Birth (Pre-discovery Stage), Discovery, Disclosure, Availability for Patching and Availability for Exploiting [8] - [10] .
Figure 1 illustrates the life cycle of vulnerability showing key stages to be discussed.
Birth (Pre-Discovery):
The birth of vulnerability occurs at the development of a software, mostly due to a weakness or a mistake in coding of the software. At this stage the vulnerability is not yet discovered or exploited. In a well-developed software package where its reliability has been identified, one can identify the probability of the birth of the problem.
Discovery:
Vulnerability is said to be discovered once someone identifies the flaw in the software. It is possible that the vulnerability is discovered by the system developers themselves, skilled legitimate users or by the attackers also. If the vulnerability is discovered internally or by white hackers, (who are making breaking attempts on a system to identify the flaws and vulnerabilities with good intentions of helping them to be patched so that the system security is strengthened) it will be notified to be fixed as soon as possible. But, if a black hacker discovers a vulnerability it is possible that he or she will try to exploit it, or sell in the black market or distribute it among hackers to be exploited.
It should be noted here that while vulnerabilities could actually exist prior to the discovery, until it is discovered, it is not a potential security risk. “Time of the discovery” is the earliest time that vulnerability is identified. In a vulnerability life cycle the “time of discovery” is an important and critical event. Exact discovery time might not be published or disclosed to the public due to the other risks that could be associated with vulnerability. However, in general after the “disclosure” of vulnerability, public may know the time of discovery subject to security risk review.
We would like to mention here that in developing our statistical model, we consider only “pre-exploit discovery”. There are rare chances that a discovery of vulnerability could occur after it is actually exploited. As an example, an attacker could run an exploit attempt aiming for a particular vulnerability but, the exploit instead break the intended system through another unidentified or undiscovered vulnerability at that time. While intending to address and incorporate such rare occurrences in our future research, in the present study we will consider vulnerabilities that we discovered before being exploited.
Disclosure:
Once a vulnerability is discovered, it is subject to be disclosed. Disclosure could take place in different ways based on the system design, authentication and who discovered it. However, “disclosure” in widely accepted form in the information security means the event that a particular vulnerability is made known to public through relevant and appropriate channels. Definition for the disclosure of vulnerability is however presented differently by different individuals.
In general, public disclosure of a vulnerability is based on several principles. The “availability of access” to the vulnerability information for the public is one such important principle. Another such important principle is “validity of information”. Validity of information principle is to ensure the user’s ability to use that information, assess the risk and take security measures. Also, the “independence of information channels” is also considered to be important to avoid any bias and interferences from organizational bodies including the vendor.
Scripting (Exploiting) and Exploit Availability:
A Vulnerability enters to the stage of “exploit availability” from the earliest time that an exploit program of code is available. Once the exploits are available even low skilled crackers (or in other words a black hat hacker) could be capable of exploiting the vulnerability. As we mentioned earlier, there are some occurrences that the exploit could happen even before the vulnerability is discovered. However in the present study we consider the modelling of Vulnerability Life Cycles with exploit availability occurs only after the discovery.
Patch Availability and Death: (Patched)
Patch is a software solution that the vendor or developer release to provide necessary protection from possible exploits of the vulnerability. Patch will act against possible exploit codes or attacking attempts for a vulnerability and protect the system and ensure the integrity. The vulnerability dies when one applies a security patch to all the vulnerable systems.
When a White Hat Researcher discovers a vulnerability, the next transition is likely to be the internal disclosure leading to patch development. On the other hand, if a Black Hat Hacker discovers a vulnerability, the next transition could be an exploit or internal disclosure to his underground community. Some active black hats might develop scripts that exploit the vulnerability. Figure 1 illustrates the process of the above discussion.
3. Methodology
3.1. Markov Chain and Transition Probabilities
A discrete type stochastic process 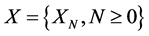 is called a Markov chain [11] if for any sequence
is called a Markov chain [11] if for any sequence 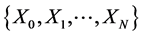 of states, the next state depends only on the current state and not on the sequence of events that preceded it, which is called the Markov property. Mathematically, we can write this property as presented
of states, the next state depends only on the current state and not on the sequence of events that preceded it, which is called the Markov property. Mathematically, we can write this property as presented
![]()
Figure 1. The life cycle of vulnerability [3] .
in Equation (1) below.
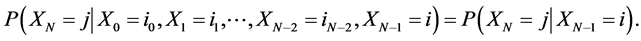 (1)
(1)
We will also make the assumption that the transition probabilities  do not depend on time. This is called time homogeneity. The transition probabilities (Pi,j)for Markov chain can be defined as follows.
do not depend on time. This is called time homogeneity. The transition probabilities (Pi,j)for Markov chain can be defined as follows.
 ,
,
That is the probability of being in state j given that we were in state i.
The transition matrix P of the Markov chain is the N × N matrix whose 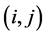 entry
entry 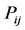 satisfied the following properties.
satisfied the following properties.
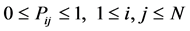 (2)
(2)
and
 (3)
(3)
Any matrix satisfying Equations ((2) and (3)) above is a Transition Probability Matrix for a Markov chain.
To simulate a Markov chain, we need its stochastic matrix P and an initial probability distribution πo.
Here, we shall simulate an N-state Markov chain (X; P; π0) for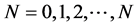 , time periods. Let X be a vector of possible state values from sample realizations of the chain. Iterating on the Markov chain we will produce a sample path {XN} where for each N, XN Î X. When writing a simulation program this is about using uniformly distributed U [0, 1] random numbers to obtain the corrected probability distribution in every step.
, time periods. Let X be a vector of possible state values from sample realizations of the chain. Iterating on the Markov chain we will produce a sample path {XN} where for each N, XN Î X. When writing a simulation program this is about using uniformly distributed U [0, 1] random numbers to obtain the corrected probability distribution in every step.
3.2. Transient States
Let P be the probability transition matrix [11] for Markov chain Xn. A “state i” is called transient state if with probability 1 the chain visits i only a finite number of times. Let Q be the sub matrix of P which includes only the rows and columns for the transient states. The transition matrix for an absorbing Markov chain has the following canonical form.
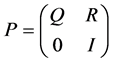 . (4)
. (4)
Here in Equation (4), P is the transition matrix, Q is the matrix of transient states, R is the matrix of absorbing states and I is the identity matrix.
The matrix P represents the transition probability matrix of the absorbing Markov chain. In an absorbing Markov chain the probability that the chain will be absorbed is always 1. Hence, we have
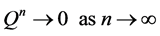 .
.
Thus, is it implies that all the eigenvalues of Q have absolute values strictly less than 1. Hence, 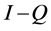 is an invertible matrix and there is no problem in defining the matrix
is an invertible matrix and there is no problem in defining the matrix
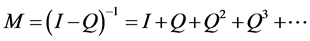 . (5)
. (5)
This matrix M in Equation (5) is called the Fundamental Matrix of P. Let i be a transient state and consider![]() , the total number of visits to state i. Then we can show that the expected number of visits to state i starting at state j is given by
, the total number of visits to state i. Then we can show that the expected number of visits to state i starting at state j is given by ![]() the
the ![]() entry of the matrix M.
entry of the matrix M.
Therefore, if we want to compute the expected number of steps until the chain enters a recurrent class, assuming starting at state j, we need only sum ![]() over all transient states i.
over all transient states i.
4. Vulnerability Life Cycle Analysis Method
4.1. Vulnerability Life Cycle Graph
The core component of the Vulnerability Life Cycle Analysis method we propose here is the Life Cycle Graph [4] . When we draw a Life Cycle Graph for a given vulnerability it has several nodes which represent the Vulnerability Life Cycle stages. We can assign a possible probability to reach each state by examining the properties of a specific vulnerability. Also, a Life Cycle Graph has two absorbing states [11] - [13] that are named “Patched state” and “Exploited state” [3] [4] . Therefore, this allows us to model the Life Cycle Graph as an absorbing Markov chain.
The Markov Model Approach to Vulnerability Life Cycle we develop is given in Figure 2. In this figure, we present a Markov approach of Vulnerability Life Cycle with five states. It should be noted that the states three and five are absorbing states of this Life Cycle Graph as there are no out flaws from those states.
We define,
![]() = the probability of transferring state i to state j.
= the probability of transferring state i to state j.
In actual situations the probability of discovering a vulnerability can be assumed very small. Therefore, for ![]() we can assign a small value. Then we assigned probabilities to
we can assign a small value. Then we assigned probabilities to![]() , accordingly.
, accordingly.
Using these transition probabilities we can derive the absorbing transition probability matrix for a Vulnerability Life Cycle, which follows the properties defined under Markov Chain Transformation Probability Method.
4.2. Transition Matrix for Vulnerability Life Cycle
Thus, we can write the transition probability matrix for vulnerability life cycle as follows.
![]()
Figure 2. Markov model approach to vulnerability life cycle with five states.
![]()
where,
![]() - Probability that the system is in state i at time t.
- Probability that the system is in state i at time t.
For ![]() we have
we have
![]() , Probability that the system is in State 1 at the beginning (
, Probability that the system is in State 1 at the beginning (![]() ).
).
![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Therefore, the initial probability can be given as![]() , that is, the probabilities of each state of the Vulnerability Life Cycle initially. It is clear that, the “State 1” (Not Discovered) with probability of one represents that at the initial time (for t = 0), the Vulnerability is not yet been discovered and therefore the probabilities for all others stages are zero.
, that is, the probabilities of each state of the Vulnerability Life Cycle initially. It is clear that, the “State 1” (Not Discovered) with probability of one represents that at the initial time (for t = 0), the Vulnerability is not yet been discovered and therefore the probabilities for all others stages are zero.
We can assign some reasonable values to![]() ’ s and create the transformation matrix P as follows. As an example, if we consider a time intervals of days, for probabilities of each stage to a specific vulnerability can be derived using the Markov process as follows.
’ s and create the transformation matrix P as follows. As an example, if we consider a time intervals of days, for probabilities of each stage to a specific vulnerability can be derived using the Markov process as follows.
For![]() , we have
, we have
![]() .
.
For![]() , results in
, results in
![]() .
.
For![]() , we can write
, we can write
![]() ,
,
And thus, for = n, we have
![]() .
.
Using this method, we can find the pattern of probability that is changing with time and is related to each “state” and then to work on finding the statistical model that can fit the vulnerability life cycle.
For![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() transition probability matrix can be written as follows:
transition probability matrix can be written as follows:
![]()
As we execute this algorithm, the stationarity was reached (considering to 4 decimal digits) at![]() , that is at
, that is at![]() , we can find the minimum number of steps so that the vulnerability reaches its absorbing states and the resulting vector of probabilities for each of the states is obtained as follows. As the row vector presents, the transition probabilities are completely absorbed into the two absorbing states which gives the probability of the vulnerability that is being exploited and the probability of the vulnerability will be patched. All other states have reached the probability of zero. That is,
, we can find the minimum number of steps so that the vulnerability reaches its absorbing states and the resulting vector of probabilities for each of the states is obtained as follows. As the row vector presents, the transition probabilities are completely absorbed into the two absorbing states which gives the probability of the vulnerability that is being exploited and the probability of the vulnerability will be patched. All other states have reached the probability of zero. That is,
![]()
The following figures illustrate the behavior of the probabilities as a function of time with respect to the different states. For states one, three, four and five taking initial probabilities as mentioned above, the behavior as a function of time is graphed. For states one and three the probability of “Not-discovered” and “Disclosed not patched” respectively, decreases with respect to time and approach zero eventually.
Figure 3 presents the behavior of the probability of each state based on the initial probabilities we assigned. It is clear that the probability of being in the state 1 decreases and approach zero eventually. This indicates that the probability of a vulnerability being “Not-discovered” over the time is decreasing and eventually reaches zero at the time of the “discovery” (Figure 3(a)). Once a vulnerability is discovered, the probability of being “Exploited” over time indeed increases. And as the system security activities also will immediately take place, the probability of being “Patched” also increases. This behavior is presented in Figure 3(b) and Figure 3(d), respectively. There is also a time gap between the disclosure and patching of the vulnerability. Initially, the probability of the vulnerability being “Disclosed not patched” will rise for a very short period of time then will decrease eventually as this is not an absorbing state in the life cycle.
For a better understanding, comparison and to have a more generalize observation we proceed to check the behavior of these probabilities over the time with different probability assigned values. We change λ1 values and compare the probability changes in each state with time. The following graphs, illustrate the behavior of each state for λ1 = 0.1, 0.2, 0.4, 0.5 and 0.7. Figure 4(a) and Figure 4(b) represent those behaviors graphically. Each graph presents the behavior of the probability of being in that “state” of the life cycle over time. It is interesting to observe that the initial probability that we assign for λ1 did not really affect much on the behavior of the probability over time.
However, it is important to note that a vulnerability with a higher initial probability of being “discovered” will go to stationarity faster than to those with a lower initial probability of being “discovered”. This is observable from the graphs labeled “Probability of being Exploited as a function of time” and “Probability of being Patched as a function of time” in Figure 4(a) and Figure 4(b) respectively.
5. The Risk Factor and Parametric Model
5.1. Introducing the Risk Factor and Evaluating the Risk Level as a Function of Time
Vulnerabilities which have been discovered but not patched represents a security risk [14] - [16] which can lead to considerable financial damage or loss of reputation (credibility).Therefore estimating the risk is very important and in the present study we introduce a method to evaluate the risk level [3] [4] of discovered vulnerabilities [16] .
By examining Figure 3 we discussed above, that is related to the state “Exploited” in the Vulnerability Life Cycle, we can clearly see the pattern of exploitability as a function of time. As a function of time, the probability
![]()
Figure 3. Behavior of the probability of different states as a function of time.
![]()
Figure 4. (a) Comparison of the behavior of the probabilities of different states with different initial probabilities for the discovery; (b) Comparison of the behavior of the probabilities of different states with different initial probabilities for the discovery.
of being exploited increases significantly up to some stage and then eventually become stable.
To evaluate the risk factor [4] of exploiting with respect to the time we consider the changes in the probability and also the CVSS score of a specific vulnerability. We explore the use of the CVSS vulnerability metrics which are publically available and are being used for ranking the strength of all vulnerabilities.
Let’s proceed to define the risk factor as follows:
Let, vi be any specific vulnerability. Then,
![]() (6)
(6)
We shall use this definition of the Risk Factor in developing our proposed statistical model to evaluate the risk behavior.
5.2. Development of a Parametric Model to Predict the Probability of Vulnerability Being Exploited
To accomplish our objective, we developed two statistical models where the response variable Y is the probability of being exploited and is driven by the attributable variable , the time. At first, for statistical accuracy to homogenize the variance we filtered the data using natural logarithm,![]() . For the second model, to obtain a better fit to the data we introduce a term with an inverse transformation in addition to the filter using the natural logarithm.
. For the second model, to obtain a better fit to the data we introduce a term with an inverse transformation in addition to the filter using the natural logarithm.
Thus, the proposed final forms of the statistical model to estimate the probability of being exploited at time t is given in the table below.
For![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() values we proposed a model to predict the probability at different time intervals as follows.
values we proposed a model to predict the probability at different time intervals as follows.
As an example, let’s take a specific vulnerability labeled as CVE-2016-0467. This has CVSS Base score 4.00, which categorized as medium score with “Impact sub score: 2.9” and “Exploitability sub score: 8.0”. For This vulnerability we can measure risk as follows.
![]() (7)
(7)
Using equation (7) above, we can predict the risk factor of specific vulnerability at any time interval.
This is an excellent model that gives us an ![]() of 0.8526 and
of 0.8526 and ![]() of 0.8507. The
of 0.8507. The![]() , named Coefficient of Determination tells us how much can the change in the response variable be explained and predicted by the attributable variables of the model and considered as the key criterion in evaluating the quality of a model. In other words,
, named Coefficient of Determination tells us how much can the change in the response variable be explained and predicted by the attributable variables of the model and considered as the key criterion in evaluating the quality of a model. In other words, ![]() equals to the ratio of the Sum of Squares of the Regression to the Total Sum of Squares. That is,
equals to the ratio of the Sum of Squares of the Regression to the Total Sum of Squares. That is,
![]() . (8)
. (8)
Let’s consider an example to illustrate these two models further. For the given values for ![]() to
to ![]() given above, consider the values of the response variable Y (Probability of being exploited) at several values of time t. Table 1 presents two model equations we have developed with respective R2 values. Table 2 illustrates several results obtained and we can obtain the Sum of Squared Error for the model using such data.
given above, consider the values of the response variable Y (Probability of being exploited) at several values of time t. Table 1 presents two model equations we have developed with respective R2 values. Table 2 illustrates several results obtained and we can obtain the Sum of Squared Error for the model using such data.
While the second model qualify to be much better as ![]() is higher compared to the first model as we mentioned previously, it should be noted here that our comparison with respect to the probability of being exploited is in comparison with the probability obtained from our transition metrics for a particular time t.
is higher compared to the first model as we mentioned previously, it should be noted here that our comparison with respect to the probability of being exploited is in comparison with the probability obtained from our transition metrics for a particular time t.
We can generate such set of models for different vulnerabilities involving different CVSS score and improve further for predicting probabilities with respect to critical stages in Vulnerability Life Cycle of a particular Vulnerability.
![]()
Table 1. Proposed models for estimating the probability of being exploited at time t.
![]()
Table 2. Probabilities estimated using two models for several values of time, t.
6. Conclusions
Using of the Markov Model Approach to Vulnerability Life Cycle, we can have a better understanding of the behavior of vulnerability as a function of time. In the present study, we have developed a successful statistical model to estimate the probability of being in a certain stage of a particular vulnerability in its life cycle. In Sections 3 and 4, we have presented our methodology of using the Markov Approach and Life Cycle Graph Analysis. This analysis with the application of Markov Chain Theory gave us the basis for calculating estimates for probabilities for different stages of a life cycle of the vulnerability considered.
Further in Section 5, we have also developed a “RISK FACTOR”, and statistical models to estimate the risk for a particular vulnerability being exploited combining our methodology with the exploitability score given in the CVSS score. Using the developed method, we can evaluate the risk level of a particular vulnerability at a certain time.
These developments ensure us with a great advantage in taking measures to avoid exploitations and introduce patches for the vulnerability before attacker takes the advantage of that particular vulnerability.
NOTES
![]()
*Corresponding author.