Special Matrices in Constructing Mutually Unbiased Maximally Entangled Bases in C2⊗C4 ()

Subject Areas: Algebra, Quantum Mechanics, Theoretical Physics

1. Introduction
Mutually unbiased maximally entangled bases (MUMEBs) are an interesting topic combining mutually unbiased bases (MUBs) and maximally entangled states. Mutually unbiased bases play an central role in quantum kinematics [1] , quantum state tomography [2] - [4] and many tasks in quantum information processing, such as quantum key distribution [5] , cryptographic protocols [6] [7] , mean king problem [8] , quantum teleportation and superdense coding [9] - [11] . Maximally entangled state is central both to the foundations of quantum mechanics and to quantum information and computation [12] - [24] .
A state 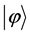 is said to be a
is said to be a 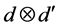 (
(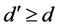 ) maximally entangled state if and only if for an arbitrary given orthonormal complete basis
) maximally entangled state if and only if for an arbitrary given orthonormal complete basis 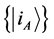 of subsystem A, there exists an orthonormal basis
of subsystem A, there exists an orthonormal basis 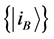 of subsystem B such that
of subsystem B such that 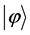 can be written as
can be written as 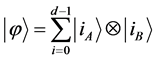 [24] . Two orthonormal bases
[24] . Two orthonormal bases 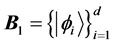 and
and 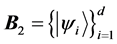 of
of 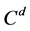 are mutually unbiased if and only if
are mutually unbiased if and only if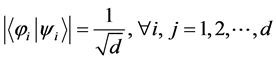 . A set of
. A set of
orthonormal bases 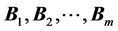 in
in  are said to be a set of mutually unbiased bases if every pair of bases in the set is mutually unbiased.
are said to be a set of mutually unbiased bases if every pair of bases in the set is mutually unbiased.
Mutually unbiased bases are recently combined with other bases, such as product basis (PB) [25] , unextendible product basis (UPB) [26] , unextendible maximally entangled basis (UMEB) [27] - [32] and maximally entangled basis (MEB) [33] - [35] . The MEB is a set of orthonormally maximally entangled states in ![]() consisting of
consisting of ![]() vectors. In [33] - [35] , by systematically constructing MEBs, the concrete construction of pairs of
vectors. In [33] - [35] , by systematically constructing MEBs, the concrete construction of pairs of
MUMEBs in bipartite systems ![]() is studied.
is studied.
In this note, we study the problem of constructing more than two mutually unbiased maximally entangled bases in bipartite spaces![]() . Through the sufficient and necessary conditions of two maximally entangled bases to be mutually unbiased, we find the special matrices and present steps of using special matrix to construct five mutually unbiased maximally entangled bases in
. Through the sufficient and necessary conditions of two maximally entangled bases to be mutually unbiased, we find the special matrices and present steps of using special matrix to construct five mutually unbiased maximally entangled bases in![]() .
.
2. Main Results
We first recall the sufficient and necessary conditions of two maximally entangled bases to be mutually unbiased in![]() .
.
Let ![]() be the orthonormal basis in
be the orthonormal basis in![]() ,
, ![]() and
and ![]() be two othonormal bases in
be two othonormal bases in![]() , A denotes the transition matrix between them, that is
, A denotes the transition matrix between them, that is![]() , i.e.,
, i.e., ![]() ,
, ![]() are entries of the matrix A.
are entries of the matrix A.
We first consider two MEBs in ![]() [33] as follows:
[33] as follows:
![]() (1)
(1)
![]() (2)
(2)
where ![]() are Pauli matrices and
are Pauli matrices and![]() .
.
From [33] , the above two MEBs (1) and (2) in ![]() are mutually unbiased if and only if the matrices A satisfy the following relations:
are mutually unbiased if and only if the matrices A satisfy the following relations:
![]() (3)
(3)
where ![]() and
and ![]() denotes
denotes ![]() mod 2.
mod 2.
To visualize the conditions (3), we divide the transition matrix A into 4 submatrices of 2 × 2 from left to right, then the conditions (3) hold if and only if each 2 × 2 submatrix satisfying the similar conditions as follows (we might take the upper left submatrix as a representative):
![]() (4)
(4)
From [33] , it is easy to find matrices satisfying the above conditions (4) such as
![]()
In this note, we want to find more than two MUMEBs, so how to find the third MEB mutually unbiased with the above two MEBs (1) and (2), it depends on the property transit matrix satisfied. Suppose that
![]() be the third orthonormal basis in
be the third orthonormal basis in![]() , and B denotes the transition matrix between
, and B denotes the transition matrix between ![]() and
and![]() , that is
, that is![]() , i.e.
, i.e.![]() ,
, ![]() are entries of the matrix B. Then ac-
are entries of the matrix B. Then ac-
cording to [33] , we have the third MEB as follows
![]() (5)
(5)
Then, the above three MEBs in ![]() are mutually unbiased if and only if the matrices A, B and BA all satisfy the conditions (4) simultaneously.
are mutually unbiased if and only if the matrices A, B and BA all satisfy the conditions (4) simultaneously.
Since the transit matrix A is easy to choose, we really want to know the way to construct matrix B. Assume that
![]()
where P is a 2 × 2 matrix, if A is known, how can we choose the matrix P to assure B and BA all satisfy the conditions (4)? For simplicity, we can first assume that P be a diagonal block matrix
![]() (6)
(6)
then we have
![]() (7)
(7)
Since B satisfy the conditions (4), then we have
![]() (8)
(8)
thus we must have
![]()
It follows from the unitarity of matrix P that
![]() (9)
(9)
Similarly, we can have
![]() (10)
(10)
so there are many choices about the values of![]() . To avoid the trivial diagonal case of matrix P, we may take
. To avoid the trivial diagonal case of matrix P, we may take![]() , then the values of
, then the values of ![]() can be divided into the following two cases:
can be divided into the following two cases:
![]()
We first discuss the case I. Obviously, there are many forms of P satisfying the above property, such as
![]() (11)
(11)
No loss of generality, we first choose
![]() (12)
(12)
then we have
![]()
It is direct to verify that the transformation matrix B and BA both satisfy the conditions (4), then the MEBs (1), (2) and (5) in ![]() are mutually unbiased.
are mutually unbiased.
Let![]() , then
, then
![]()
Denoting ![]() be the fourth orthonormal basis in
be the fourth orthonormal basis in![]() , and C denotes the transition matrix between
, and C denotes the transition matrix between ![]() and
and![]() , that is
, that is![]() , then the fourth MEB in
, then the fourth MEB in ![]() can be con-
can be con-
structed as follows:
![]() (13)
(13)
Obviously, ![]() ,
, ![]() and
and
![]()
It is easy to check the above matrices C, ![]() and
and ![]() all satisfy the conditions (4), so the fourth MEB (13) is mutually unbiased with the former three bases (1), (2) and (5) in
all satisfy the conditions (4), so the fourth MEB (13) is mutually unbiased with the former three bases (1), (2) and (5) in![]() .
.
Moreover, let![]() , then
, then
![]()
Denoting ![]() be the fifth orthonormal basis in
be the fifth orthonormal basis in![]() , and
, and ![]() denotes the transition matrix between
denotes the transition matrix between ![]() and
and![]() , that is
, that is![]() , then the fourth MEB in
, then the fourth MEB in ![]() can be constructed as follows:
can be constructed as follows:
![]() (14)
(14)
Obviously, ![]() ,
, ![]() ,
, ![]() and
and
![]()
One can directly check that the above matrices![]() ,
, ![]() ,
, ![]() and
and ![]() all satisfy the conditions (4), so the fifth MEB (14) is mutually unbiased with the former four bases (1), (2), (5) and (13) in
all satisfy the conditions (4), so the fifth MEB (14) is mutually unbiased with the former four bases (1), (2), (5) and (13) in![]() .
.
Furthermore, let![]() , then
, then
![]()
Denoting ![]() be the fifth orthonormal basis in
be the fifth orthonormal basis in![]() , and
, and ![]() be the transition matrix between
be the transition matrix between ![]() and
and![]() , that is
, that is![]() , then
, then ![]() and
and
![]()
Since ![]() is exactly equal to A, the sixth orthonormal basis
is exactly equal to A, the sixth orthonormal basis ![]() is equal to
is equal to![]() , thus using matrix p, we can only get five MUMEBs (1), (2), (5), (13), (14) and no the sixth one.
, thus using matrix p, we can only get five MUMEBs (1), (2), (5), (13), (14) and no the sixth one.
Next, we discuss Case II of![]() . Now there are many forms of P satisfying the property, such as
. Now there are many forms of P satisfying the property, such as
![]()
If we take the same A in (12) and choose the following form of P:
![]()
similar to the above analysis, we can get the five MUMEBs in ![]() in [33] .
in [33] .
3. Conclusion
In this note, we have constructed five mutually unbiased maximally entangled bases in bipartite spaces ![]() using special matrices. Thus, we have presented a method to construct more than two mutually unbiased maximally entangled bases in
using special matrices. Thus, we have presented a method to construct more than two mutually unbiased maximally entangled bases in![]() . Similar problems can be discussed in arbitrary bipartite spaces
. Similar problems can be discussed in arbitrary bipartite spaces![]() .
.
NOTES
![]()
*Corresponding author.