Stability and Regularization Method for Inverse Initial Value Problem of Biparabolic Equation ()
Subject Areas: Numerical Mathematics, Partial Differential Equation
1. Introduction
Let H be a complex separable Hilbert space endowed with the inner product 
and the norm
, and 
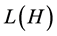be the Banach algebra of bounded linear operators on H. Denote 
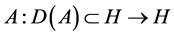as a positive and self-adjoint operator with compact resolvent; 
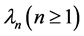is the real eigenvalues of A; 
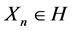is the corresponding orthonormal basis of eigenvectors, and 
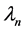satisfies
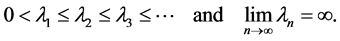(1)
This paper considers the inverse initial value problem for the biparabolic equation
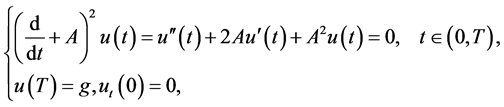(2)
our purpose is to reconstruct the initial value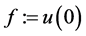 
from the final measured data
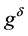; here 
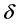denotes the noisy level.
In past years, many authors have considered the inverse initial value problem of classical parabolic equation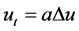 
with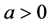 
(see [1] - [4] , etc.). However, it is well-known that the classical parabolic equation can not accurately describe the procedure of heat conduction [5] [6] , so many models have been proposed to describe this procedure; among them the biparabolic model proposed in [7] can give a more adequate mathematical description for the process of heat conduction than the classical case. Meanwhile we note that, for the biparabolic model, up to now the literatures devoted to it are relatively scarce, except for [7] - [9] . On other models, we can see [10] - [13] , etc.
Problem (2) is ill-posed and the regularization techniques are required to stabilize numerical computations [14] [15] . In 2015, [9] considered this problem and proved a condition stability result of Hölder type, and then applied the Kozlov-Maz’ya iteration method to deal with it; the corresponding convergence results have been given, but unfortunately the condition stability result in [9] is not useful for the case of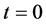
. In this paper, we firstly establish a conditional stability of Hölder type, which is valid at the point
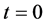, then use a modified regularization method to overcome its ill-posedness and give the convergence estimate under an a-priori assumption for the exact solution. On the similar references for this regularization method, we can refer to [16] - [18] , etc.
This paper is constructed as follows. In Section2, we establish the conditional stability of Hölder type for this problem, then use a modified regularization method to deal with it and derive the convergence estimate under an a-priori assumption for the exact solution in Section 3. Numerical results are given in Section 4. Some conclusions are made in Section 5.
2. The Ill-Posedness and Conditional Stability Estimate
From [9] , we know that the unique formal solution of problem (2) can be expressed as
![]()
(3)
It can be noticed that, for![]()
, ![]()
tends to infinity as![]()
, so in order to recovery
the stability of solution ![]()
given by (3), the coefficient ![]()
must decay rapidly. However, such a decay usually cannot occur for the measured data![]()
, thus we have to use a regularization technique to restore numerical stability.
Note that,
![]()
(4)
In general, under an additional a-priori bound assumption, a stability of the solution on the data can be obtained, this is called the conditional stability. Let![]()
, ![]()
, here we assume the exact solution ![]()
satisfy the a-priori condition
![]()
(5)
now we give a conditional stability estimate of Hölder type for![]()
.
Theorem 2.1. Let f given by (4) is the exact solution of problem (2) with the exact data g, assume the a priori bound (5) is satisfied, then we have the following stability result
![]()
(6)
where,![]()
.
Proof. Using (4), Hölder inequality, (5), we have
![]()
from the above estimate, the conditional stability result (6) can be established.
3. Regularization Method and Convergence Estimate
Let the exact and noisy data ![]()
and satisfy
![]()
(7)
where ![]()
denotes the H-norm. Based on the ill-posedness analysis in Section 2, we define the following modified regularization solution
![]()
(8)
here, ![]()
plays a role of the regularization parameter. In the following, we give the convergence estimate under an a-priori assumption for the exact solution f.
Theorem 3.1. Suppose that f given by (4) is the exact solution of problem (2) with the exact data g at![]()
, ![]()
is the regularization solution defined by (8) with the measured data![]()
. Let the measured data ![]()
satisfy (7), and the a priori bound (5) is satisfied. If the regularization parameter is chosen as
![]()
(9)
then we have the following convergence estimate
![]()
(10)
Proof. For![]()
, we define the function
![]()
(11)
it is easy to verify that ![]()
has a unique maximizer ![]()
as ![]()
such that
![]()
(12)
Note that
![]()
(13)
We firstly give a estimate for I1. By (4), (5), (7), (8), using (12) and the fact![]()
, we get
![]()
Below, we estimate![]()
. Using (4), (5), (8) with the exact data g, (12) and the inequality
![]()
, one can obtain that
![]()
From the above estimates of![]()
, ![]()
, and combining with (9), the triangle inequality (13), we can obtain the convergence result (10).
4. Numerical Implementations
In this section, we use a numerical example to verify how this method works for the reconstruction of initial data f. Consider the following forward problem
![]()
(14)
where![]()
, ![]()
with the domain![]()
, its eigenvalue and the eigenfunction are![]()
, ![]()
, respectively.
By the method of separation of variables, it is easy to obtain that the solution of problem (14) can be expressed as
![]()
(15)
where,![]()
. We take the exact data as
![]()
(16)
the measured data is chosen as![]()
, where ![]()
is the error level.
In the computational procedure, the exact and regularization solutions are computed by (4), (8), respectively. The regularization parameter ![]()
is chosen by (9) with![]()
. For![]()
, the numerical results for![]()
, ![]()
constructed from ![]()
with ![]()
are shown in Figure 1. For![]()
, the numerical results for![]()
, ![]()
constructed from ![]()
are shown in Figure 2.
From Figure 1 and Figure 2, we can see that this method is effective and feasible. Figure 1 indicates that, with the increase of T, the construction effects become worse, this is because the information of final value data will become less when T becomes big. Figure 2 shows that the smaller ![]()
is, the better the computed efficiency is, this is a normal phenomena in the inverse initial value problem of parabolic equation.
5. Conclusion
An inverse initial value problem of the biparabolic equation is investigated. We firstly establish a conditional stability of Hölder type for this problem, then use a modified regularization method to regularize it and derive
the convergence estimate under an a-priori assumption for the exact solution. Numerical results show that this method is stable and feasible.
Acknowledgements
The authors thank for the careful work of the anonymous referee and the suggestions that improved the quality for our paper. This work is supported by the SRF (2014XYZ08), NFPBP (2014QZP02) of Beifang University of Nationalities, the SRP of Ningxia Higher School (NGY20140149) and SRP of State Ethnic Affairs Commission of China (14BFZ004).