{C_k, P_k, S_k} -Decompositions of Balanced Complete Bipartite Multigraphs

Jenq-Jong Lin¹, Min-Jen Jou²

¹Department of Finance, Ling Tung University, Taichung City.
²Department of Information Technology, Ling Tung University, Taichung City.

DOI: 10.4236/ojdm.2016.63015                

Abstract

Let be a family of subgraphs of a graph G. An L-decomposition of G is an edge-disjoint decomposition of G into positive integer copies of H_i, where . Let C_k, P_k and S_k denote a cycle, a path and a star with k edges, respectively. For an integer , we prove that a balanced complete bipartite multigraph  has a -decomposition if and only if k is even, and .

Keywords

Balanced Complete Bipartite Multigraph, Cycle, Path, Star, Decomposition

Received 16 June 2016; accepted 11 July 2016; published 14 July 2016

1. Introduction

Let F, G and H be graphs. A G-decomposition of F is a partition of the edge set of F into copies of G. If F has a G-decomposition, we say that F is G-decomposable. Let 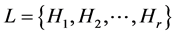be a family of subgraphs of a graph G. An L-decomposition of G is an edge-disjoint decomposition of G into positive integer 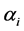copies of, where. If G has an L-decomposition, we say that G is L-decomposable.

For positive integers m and n, denotes the complete bipartite graph with parts of sizes m and n. A complete bipartite graph is balanced if. A k-cycle, denoted by, is a cycle of length k. A k-star, denoted by, is the complete bipartite graph. A k-path, denoted by, is a path with k edges. For a graph G and an integer, we use to denote the multigraph obtained from G by replacing each edge e by edges each of which has the same ends as e.

Decompositions of graphs into k-stars have also attracted a fair share of interest (see [1] - [3] ). Articles of - decompositions of interest include [4] [5] . Decompositions of some families of graphs into k-cycles have been a popular topic of research in graph theory (see [6] [7] for surveys of this topic). The study of -decom- position was introduced by Abueida and Daven in [8] . Abueida and Daven [9] investigated the problem of -decomposition of the complete graph. Abueida and O’Neil [10] settled the existence problem for -decomposition of the complete multigraph for. In [11] , Priyadharsini and Muth- usamy gave necessary and sufficient conditions for the existence of a -factorization of where. Furthermore, Shyu [12] investigated the problem of decomposing into paths and stars with k edges, giving a necessary and sufficient condition for. In [13] , Shyu considered the existence of a decomposition of into paths and cycles with k edges, giving a necessary and sufficient condition for. Shyu [14] investigated the problem of decomposing into cycles and stars with k edges, settling the case. Recently, Lee [15] [16] established necessary and sufficient conditions for the existence of a -decomposition of a complete bipartite graph and -decomposition of a balanced complete bi- partite graph. Lin and Jou [17] investigated the problems of the -decomposition of the balanced complete bipartite graph. It is natural to consider the problem of the -decomposition of the balanced complete bipartite multigraph for. In this paper, the necessary and sufficient conditions for the existence of such decomposition are given.

2. Preliminaries

Let G be a graph. The degree of a vertex x of G, denoted by, is the number of edges incident with x. The vertex of degree k in is the center of. For and, we use and to denote the subgraph of G induced by A and the subgraph of G obtained by deleting B, respectively.

When are graphs, not necessarily disjoint, we write or for the graph with vertex set and edge set. When the edge sets are disjoint,

expresses the decomposition of G into. is the short notation for the union of n copies of disjoint graphs isomorphic to G. Let H be a subgraph of with vertex set and edge set, and let r be a nonnegative integer. We use to denote the graph with vertex set and edge set where the subscripts of b are taken modulo n. For any vertex x of a digraph G, the outdegree (respectively, indegree) of x is the number of arcs incident from (respectively, to) x. A multistar is a star with multiple edges allowed. We use to denote a multistar with k edges. Let G be a multigraph. The edge-multiplicity of an edge in G is the number of edges joining the vertices of the edge. The multiplicity of G, denoted by, is the maximum edge- multiplicity of G.

Lemma 1. ( [3] ) For integers m and n with, the graph has an -decomposition if and only if and

Lemma 2. ( [18] ) Suppose that. Then is -decomposable.

Let denote the edge ab in the s-th copy of for.

Lemma 3. If k is an even integer with, then there exist edge-disjoint 2k-cycles in.

Proof. A decomposition of into 2k-cycles is given by the following cycles:, where, and. □

Note that can be decomposed into two copies of k-paths:

and, that

is, can be decomposed into copies of k-paths.

Lemma 4. ( [4] ) There exists a -decomposition of if and only if, and one of the following (see Table 1) cases occurs.

Lemma 5. ( [19] ) For positive integers m, n and k, the graph has a -decomposition if and only if and k are even, , , and.

Table 1. The conditions of a -decomposition of.

3. Main Results

With the results ( [17] ) of the -decomposition of the balanced complete bipartite graph, it is assumed that in the sequel. In this section, we will prove the following result.

Main Theorem. Let k and n be positive integers. The graph has a -decomposition if and only if k is even, and.

We first give necessary conditions for a -decomposition of.

Lemma 6. If has a -decomposition, then k is even, and.

Proof. Since bipartite graphs contain no odd cycle, k is even. In addition, the minimum length of a cycle and the maximum size of a star in are 4 and n, respectively, we have. Finally, the size of each member in the decomposition is k and; thus. □

Throughout this paper, let denote the bipartition of, where and. We now show that the necessary conditions are also sufficient. The proof is divided into cases, , and, which are treated in Lemmas 7, 8, and 9, respectively.

Lemma 7. For an even integer, then has a -decomposition.

Proof. Note that. By Lemmas 1 and 4, has a -decomposition and a -decomposition. In addition, by Lemma 5, has a -decomposition. Hence has a -decomposition. □

Lemma 8. Let k be a positive even integer and let n be a positive integer with. If is divisible by k, then has a -decomposition.

Proof. Let. From the assumption, we have. Let. Since, we have, which implies that t is a positive integer. The proof is divided into two cases according to the values of t.

Case 1..

Let, ,

and.

Clearly. Note that G is isomorphic to, is isomorphic to, is isomorphic to and F is isomorphic to, which can be decomposed into copies of by Lemmas 1 and 2. In the following, we will show that can be decomposed into copies of, one copy of and copies of.

Let, where and. Define a subgraph W of G as follows:

and the subscripts of b are taken modulo k. Note that for t is even, and

for t is odd, this assures us that there are enough edges for W. Note that a can be decomposed into 2 copies of. In addition, for t is even as well as for t is odd, it follows that W can be decomposed into t copies of. Since, we

interchange two edges in and in, then we obtain a new cycle

. Hence can be decomposed into

copies of and one copy of.

Let be the graph obtained from G by deleting the edges in W. For the case of t is even, we have that

The other case of t is odd, we have that

Let for. Then for t is even, and for t is odd

with the center at.

In the following, we will show that can be decomposed into r copies of with centers in, and into k copies of with centers in for t is even as well as k/2 copies

of with centers in and copies of with centers in for t

is odd, that is, there exists an orientation of such that

(1)

where, and for t is even

(2)

where, and for t is odd

(3)

We first consider the edges oriented outward from. If t is even, then the edges

are all oriented outward from where. If t is odd, for

, the edges and

are all oriented outward from, where the subscripts of b are taken modulo r in the set. In both of the cases the subscripts of b are taken modulo r in the set of numbers. Since for t is even, and for t is odd, this assures us that there are enough edges for the above orientation. Finally, the edges which are not oriented yet are all oriented from to.

From the construction of the orientation, it is easy to see that (2) and (3) are satisfied, and for all, we have

(4)

So, we only need to check (1).

Since for, it follows from (4) that

for. Note that t is even, , and t is odd,

Thus,

Therefore for. This proves (1). Hence, there exists the required decomposition of. Let be the star with center at in for. Then is an. Since, by Lemma 2, we obtain that can be decomposed into copies of for.

Let be the -multistar with center at in for. Let

for. Then is decomposed into, ,

and each. It follows that. Since, by Lemma 2, we obtain that can be decomposed into copies of for. Recall that , we have that is -decomposable.

Case 2..

Let, ,

and.

Then. By similar arguments as in the proof of Case 1, we have that can be decomposed into one copy of and copies of. On the other hand, by Lemma 5, has a -decomposition. Hence has a -decomposition. □

Lemma 9. Let k be a positive even integer and let n be a positive integer with. If is divisible by k, then has a -decomposition.

Proof. Let where q and r are integers with. From the assumption of, we have. Note that

Trivially, , and are multiples of k. Thus

from the assumption that is divisible by k. By Lemmas 1 and 2, , and have -decomposition.

In the case of, by Lemma 7, we obtain that has a -decomposition. In addition, by Lemma 8, has a -decomposition for. Hence there exists a -de composition of. □

Now we are ready for the main result. It is obtained by combining Lemmas 6, 7, 8 and 9.

Theorem 1. Let k and n be positive integers. The graph has a -decomposition if and only if k is even, and.

Remark. Let m and n be positwe integers with. Since bipartite graphs contain no odd cycle, k is even. In addition, the minimum length of a cycle and the maximum size of a star in are 4 and m, respectively, we have. Moreover, each k-cycle in uses vertices of each partite set, which implies

that. Finally, the size of each member in the decomposition is k and, thus

. Hence the obvious necessary conditions for the graph to have a -de composition are: 1) k is even, 2), and 3). It is natural to ask whether they are sufficient.

Acknowledgements

The authors are grateful to the referees for the helpful comments.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Tazawa, S. (1985) Decomposition of a Complete Multipartite Graph into Isomorphic Claws. SIAM Journal on Algebraic Discrete Methods, 6, 413-417. http://dx.doi.org/10.1137/0606043
[2]	Ushio, K., Tazawa, S. and Yamamoto, S. (1978) On Claw-Decomposition of Complete Multipartite Graphs. Hiroshima Mathematical Journal, 8, 207-210.
[3]	Yamamoto, S., Ikeda, H., Shige-Ede, S., Ushio, K. and Hamada, N. (1975) On Claw Decomposition of Complete Graphs and Complete Bipartie Graphs. Hiroshima Mathematical Journal, 5, 33-42.
[4]	Parker, C.A. (1998) Complete Bipartite Graph Path Decompositions. PhD Dissertation, Auburn University, Auburn.
[5]	Shyu, T.W. (2007) Path Decompositions of λKn,n. Ars Combinatoria, 85, 211-219.
[6]	Bryant, D. and Rodger, C.A. (2007) Cycle Decompositions. In: Colbourn, C.J. and Dinitz, J.H., Eds., The CRC Handbook of Combinatorial Designs, 2nd Edition, CRC Press, Boca Raton, 373-382.
[7]	Lindner, C.C. and Rodger, C.A. (1992) Decomposition in Cycles II: Cycle Systems, In: Dinitz, J.H. and Stinson, D.R., Eds., Contemporary Design Theory: A Collection of Surveys, Wiley, New York, 325-369.
[8]	Abueida, A. and Daven, M. (2003) Multidesigns for Graph-Pairs of Order 4 and 5. Graphs and Combinatorics, 19, 433-447. http://dx.doi.org/10.1007/s00373-003-0530-3
[9]	Abueida, A. and Daven, M. (2004) Mutidecompositons of the Complete Graph. Ars Combinatoria, 72, 17-22.
[10]	Abueida, A. and O’Neil, T. (2007) Multidecomposition of λKm into Small Cycles and Claws. Bulletin of the Institute of Combinatorics and Its Applications, 49, 32-40.
[11]	Priyadharsini, H.M. and Muthusamy, A. (2009) -Multifactorization of . Journal of Combinatorial Mathematics and Combinatorial Computing, 69, 145-150.
[12]	Shyu, T.W. (2010) Decomposition of Complete Graphs into Paths and Stars. Discrete Mathematics, 310, 2164-2169. http://dx.doi.org/10.1016/j.disc.2010.04.009
[13]	Shyu, T.W. (2010) Decompositions of Complete Graphs into Paths and Cycles. Ars Combinatoria, 97, 257-270.
[14]	Shyu, T.W. (2013) Decomposition of Complete Graphs into Cycles and Stars. Graphs and Combinatorics, 29, 30-313. http://dx.doi.org/10.1007/s00373-011-1105-3
[15]	Lee, H.C. (2013) Multidecompositions of Complete Bipartite Graphs into Cycles and Stars. Ars Combinatoria, 108, 355-364.
[16]	Lee, H.C. and Chu, Y.-P. (2013) Multidecompositions of the Balanced Complete Bipartite Graph into Paths and Stars. ISRN Combinatorics, 2013, Article ID: 398473. http://dx.doi.org/10.1155/2013/398473
[17]	Lin, J.J. and Jou, M.J. (2016) {Ck, Pk, Sk}-Decompositions of Balanced Complete Bipartite Graphs. (Submitted)
[18]	Lin, C., Lin, J.J. and Shyu, T.W. (1999) Isomorphic Star Decomposition of Multicrowns and the Power of Cycles. Ars Combinatoria, 53, 249-256.
[19]	Sotteau, D. (1981) Decomposition of Km,n (K*m,n) into Cycles (Circuits) of Length . Journal of Combinatorial Theory, Series B, 30, 75-81.