Numerical Characterization of Harbor Oscillations in the Port of Ensenada, Mexico ()
Received 1 May 2016; accepted 8 July 2016; published 12 July 2016

1. Introduction
Ports and harbors can be used for commercial, recreational and military purpose. Compared to other kinds of transportation (railroad, airplane, highways), waterborne commerce has two significant advantages: low cost and high capacity. Many nations use waterborne commerce as a major source of transport [1] .
The Port of Ensenada (PE) is located on the west coast of the Baja California Peninsula, approximately 110 km south of the Mexico-US border, within Bahia de Todos Santos (BTS) in the City of Ensenada (Figure 1(a)). It is one of the most important height and cabotage ports in the country, with sea routes to and from major ports in Asia, North, Central and South America (http://www.puertoensenada.com.mx). The length of main rubble mound breakwater is approximately 1650 m and the wet surface area of the basin has 600,000 m2 composed of internal areas of navigation and service with a length of berthing of 6014.25 m [2] (Figure 1(b)).
It is well known that harbors with sides on the order of 500 m in length and depths on the order of 10 m are subject to a natural oscillation period on the order of 1 min and longer [3] . Natural oscillation period, T, is a fundamental property of a harbor and depends on the harbor’s geometrical parameters and depth [4] .
For a simple rectangular basin of length L and uniform depth h with an open end, harbor’s natural oscillation period T (or harbor modes) can be approximately estimated as [5] :
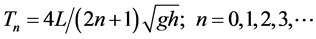 (1)
(1)
where n is the mode number. Assuming the PE dimensions as L/4 = 2350 m with uniform depth h = 9 m, the fundamental T0 mode (or Helmholtz mode) is estimated to be T0 = 16.67 min. It describes a quarter-wave oscillation with a single nodal line at the mouth and maximal amplitudes at the head. Since, this is the largest wave period among all the supported standing waves inside PE, it is clear that oscillations of larger period detected at the site would correspond to external signals.
Natural oscillation periods are independent of the external forcing, however, magnitudes of these oscillations highly depend on the external energy source that generates the oscillations [6] . Most common external forcing in harbors may be infra-gravity (IG) waves, i.e. long waves with period T > 25 s, mainly generated through nonlinear interaction of short wave groups [4] [7] [8] .
When IG waves with frequencies close to those of resonating harbor modes arrive into a harbor opening, they can be highly amplified into inner basins resulting in large oscillations of the water surface [5] [9] . These oscillations can interrupt berthing operations and affect harbor procedures. They may even damage the ship or dock facilities and cause breaking of mooring lines and fenders.
Mexican Navy (SEMAR) maintains a monitoring sea level station inside PE (its location is indicated by the yellow circle in Figure 1(b)). They provide us with sea level data, corresponding to a storm event occurred March 1-3, 2014 at the region, from which a spectral analysis was performed. The resulting spectrum is depicted
![]()
Figure 1. (a) Bahia de todos santos; (b) Port of ensenada. Yellow dot marks the sea level measuring site (modified from google earth).
in Figure 2. Since, the spectral frequency band value corresponding to 16.66−1 min−1 is practically the same as the estimated T0 mode, it is considered that energy peaks found at frequency bands f = 50−1 min−1 and 25−1 min−1 would correspond to signals generated outside the PE. The energy amplification found at bands f < 16.66−1 min−1 may result from resonance within PE. Registered maximum elevation during that event was An = 0.6 m [10] .
The response of a harbor to long waves from open sea is well described by a parameter called “Amplification Factor”, H, [5] ;
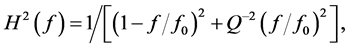 (2)
(2)
where f is the frequency of the long incoming waves, f0 is the resonant frequency of the harbor, and Q is the quality factor, which is a measure of energy damping in the system. In this study, Q was estimated according to [11] and has been set as Q = 19.18.
Harbor’s natural oscillation model, Equation (1), gives natural frequencies of the possible oscillations in an idealized rectangular basin, but it does not provides information of the response to external forcing or the spatial distribution of amplitudes within the basin [9] . Numerical models solving the primitive equations are useful for these purposes.
Previous numerical studies on the PE have been focused on wind waves and tides as forcing agents [2] [12] - [14] , letting aside long IG waves and its effects inside the port. Studies such as of this paper are important in understanding the IG period oscillations in small harbors as Port of Ensenada, and in estimating preliminary dimensions for harbor modifications in order to minimize the oscillation problem.
In this contribution, a series of numerical experiments are conducted to elucidate the response of the PE to IG wave energy. First, the Helmholtz natural mode is estimated, and then the spatial structure of amplitudes within the harbor under different frequency forcing are obtained. Finally, the spatial distribution of the associated currents is presented. The numerical experiments use a barotropic configuration of the General Curvilinear Ocean Model [15] on a boundary-fitted grid. For a given frequency, f, the model is forced by a periodic velocity field at the entrance of the PE, such that it produces an overall sea surface oscillation of 1.0 cm amplitude. This mimics the effect of remote atmospheric pressure perturbations of 1.5 hPa acting at frequency f [9] .
![]()
Figure 2. March 01-03, 2014 power spectrum at port of ensenada basin. Monitoring site is marked by the yellow dot in Figure 1(b).
2. Methodology
The GCOM Model
The simulations were carried out using the General Curvilinear Ocean Model [15] . GCOM solves the non-hy- drostatic, non-linear, full 3D time-dependent primitive variables equations in a curvilinear coordinate system and utilizes a finite difference discretization and a semi-implicit time integration scheme. GCOM is a versatile model that has been used successfully on studies of stratified flows over complex terrain ( [16] [17] . A full description of the model may be found in [15] [18] . Briefly, GCOM solves the set of dimensionless perturbed equations given by [19] ;
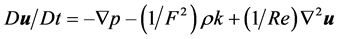 (3)
(3)
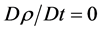 (4)
(4)
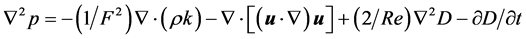 (5)
(5)
where u = (u, v, w) is the velocity vector, and i, j and k are the unit vectors in the x, y, and z coordinates respectively, p is the pressure, ρ is the water density and D(= ∇×u) represents the divergence. The dimensionless numbers are the Reynolds number, Re(= UL/ν) and the Froude number F(= U/NL), where U and L are a typical velocity and length respectively, νis the kinematic viscosity and N2 = (−g/ρ0)∂ρ/∂z is the Brünt-Väisälä frequency. As it is noted, in primitive variables, unknowns are (u, ρ, p) as indicated by Equation (1) and Equation (2), while Equation (3) substitutes the incompressibility condition given bay Ñ×u = 0.
The above set of governing equations is transformed from Cartesian to curvilinear coordinates (i.e. from physical (x, y, z) domain to computational (x, η, ζ) domain and then solved subject to initial and boundary conditions. On solid boundaries u = 0, with no flux of density, ∇ρ∙n = 0 (where n is the unit normal vector), while for p, the boundary condition is determined by substituting u = 0 into the transformed momentum Equation (3) [19] .
The geometry of the study site is well captured by using a three-dimensional boundary-fitted grid. The computational domain consists of 299 × 75 × 11 (ξ × η × ζ) grid points in the x, y and z directions with 10 m horizontal resolution, and 11 vertical layers with 1m minimum distance between points. Grid point distribution at ζ = 11 is shown in Figure 3.
![]()
Figure 3. Surface grid in physical space.
Since, GCOM is based on to pass from a physical space to a computational space through the Jacobian (J) of the transformation, then det(J) ¹ 0 in order to GCOM to perform. Physically, it means that the transformation from one plane to another has to be one-to-one. So, special careful is recommended during the grid elaboration process.
The model is forced by prescribing the velocity field:
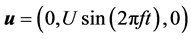
for Re = 106. Since, in this study the model was run in barotropic mode (i.e. uniform density), terms involving F were neglected and Equation (4) represents a passive scalar.
In all numerical experiments the fluid started from rest, and nearly steady solutions, defined by the convergence criterion [18] :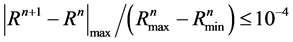 , where n is the time step and R represents any one of u or p, were obtained at a dimensionless time equivalent to 15 days of simulation. Dimensionless time increment was set to ∆t = 0.008.
, where n is the time step and R represents any one of u or p, were obtained at a dimensionless time equivalent to 15 days of simulation. Dimensionless time increment was set to ∆t = 0.008.
3. Results and Discussions
To elucidate the response of the PE basin to long IG waves, first a forcing frequency f = 50−1 min−1 is considered. The general trend of the resulting spectrum, presented in Figure 4, is very similar to that shown in (Figure 2. As expected, there is an increase of energy at the forcing frequency band. Energy peaks are also found at bands f = 25−1 min−1 and f = 16.12−1 min−1. In particular, the increase of energy at bands f = 6.28−1 min−1 and f = 3.63−1 min−1 agree remarkably well with those presented in Figure 2. There are two new secondary energy peaks at bands f = 10.2−1 min−1 and f = 8.33−1 min−1 that could be related to the first harmonics of the fundamental mode.
Resulting spectra for the numerical experiments with forcing frequency f = 30−1 min−1, f = 25−1 min−1 and f0 = 16.66−1 min−1 are shown in Figure 5. For the three experiments, the corresponding spectra presents maximum of energy at each of the forcing frequency band and also at frequency bands f = 8.33−1 min−1 and f = 4.16−1 min−1 which can be identified as the resonant frequencies f1 and f2 respectively. Notice that for f0 = 16.66−1 min−1, the energy peak is larger than the ones at f = 30−1 min−1 and f = 25−1 min−1. This is due to the fact that f0 practically coincides with the estimated resonance Helmholtz mode (T0 = 16.65 min) described already and confirms that this is the frequency of the fundamental mode of the PE. Frequency values at bands f1 and f2 correspond to L/2 = 4700 m and L/4 = 2350 m whose period, T = L(gh)−1/2, is T1 = 8.33 min and T2 = 4.16 min respectively. Thus, the spatial distribution of amplitudes for f0 describes a quarter-wave oscillation with a maximum at the head and amplitudes of the same sign within the basin which means that amplitudes oscillate in phase (Figure 6(a)). For
![]()
Figure 4. Power spectra of the simulated sea level time series at one particular location of the head of the harbor corresponding to run with forcing frequency f = 50−1 min−1.
![]()
Figure 5. Power spectra of the simulated sea level time series at one particular location of the head of the harbor corresponding to runs with forcing frequency f0 = 16.66−1 min−1 (black line), f = 30−1 min−1 (dashed blue line) and f = 25−1 min−1 (dashed black line).
f1, the spatial structure of amplitudes has two nodal lines; one at the head and another some distance away from the entrance ((Figure 6(b)), while for f2 the amplitude distribution presents three nodal lines (Figure 6(c)).
The amplification factor, H, as a function of f0 obtained for all the numerical experiments is plotted in Figure 7. As expected, the maximum value is reached at the Helmholtz frequency f0 = 16.66−1 min−1 with a Q factor of 19, and decays relatively fast as one moves away from f0. It is worth noting that the amplification factor value at f0 predicted by the model agrees very well with the Q-factor, Q = f0/Δf = 21 deduced from the spectrum of Figure 2 using a Δf of 0.91 min−1 from the figure. The similitude of Q values and the good agreement of the results with the theoretical curve, Equation (2), provide robust arguments for the good performance of the model.
Currents associated to oscillations inside a port can generate further resonance and possibly damages to the moored ships [20] . For the cases in this study, magnitude and direction of the associated currents were also obtained. The contours of magnitude of velocity associated to f0, f1 and f2 are shown in Figure 8. For f0, maxima of velocity (60 and 40 cm∙s−1) are found at the narrow passages inside PE, while at the middle and the head velocities are approximately 20 cm∙s−1 (Figure 8(a)). For f1, contours of magnitude of velocity increase at the narrow passages (80 and 120 cm∙s−1) while at the sites where the basin stretches (I, II and II, Figure 8(b)), magnitude is in the range 40 - 60 cm∙s−1. For f2, contours of minimum of magnitude are found at the head (20 cm∙s−1), relative maxima at the middle of the basin (40 - 80 cm∙s−1), and maximum values (160 cm∙s−1) some distance away from the mouth (Figure 8(c)).
Locally, under normal sea conditions, reported velocity of surface currents at the mouth and inside the PE are of the order of 20 - 40 cm∙s−1 [2] [13] [14] . In this study, for the storm event occurred March 1-3, 2014, simulated velocities at the mouth were of the order of 60 cm∙s−1, 80 cm∙s−1 and 100 cm∙s−1 for forcing f0, f1 and f2 respectively. The order of magnitude of these agree very well with the maximum velocities of 62 cm∙s−1 estimated with the relation [21]
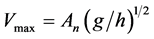
using An = 0.6 m from the observations.
Finally, in order to identify the possible source of the external signals found in the spectral analysis of this study (Figure 2), some simple calculations were made. Assuming a BTS of rectangular shape, with sides of 15 km and uniform depth of 40 m (indicated by the broken squared line in Figure 1(a), an estimation for the first three natural oscillation modes can be obtained as T0 = 50.48 min, T1 = 25.24 min and T2 = 16.82 min. Since,
![]() (a)
(a)![]()
![]() (b) (c)
(b) (c)
Figure 6. Simulated amplitudes for (a) f0 = 16.66−1 min−1; (b) f1 = 8.33−1 min−1 and (c) f2 = 4.16−1 min−1. Broken black line depicts the nodal lines.
these values are very close to those found previously in the spectral analysis presented in Figure 2 and Figure 4, it is natural to consider these latter to correspond to the first three natural modes of oscillation of the BTS.
Since, the excitation at the entrance of the PE requires the arrival of waves containing energy in the frequency band f0 = 16.66−1 cpm; BTS oscillation mode T2 = 16.82 min could be identified as the excitation source for the oscillations inside PE.
![]()
Figure 7. Amplification factor for the numerical experiments of this study (black diamonds). Solid line is the curve for f0 = 16.66−1 cpm given by Equation (2).
![]()
![]()
![]()
Figure 8. Simulated magnitude of velocity for (a) f0 = 16.66−1 min−1; (b) f1 = 8.33−1 min−1 and (c) f2 = 4.16−1 min−1.
While finishing this contribution, the author noticed the work of Rivera and Peña [22] who estimated the resonance modes of the BTS using the simple model by Dorrestein [23] , as well as spectral analysis from a time series of the BTS from May 22, 1960. They obtained natural modes of oscillation at T0 = 51.54 min, T1 = 22.88 min and T2 = 15.45 min, which agree very well to those in this study. Also their spectral analysis gave energy peaks at frequency bands f1 = 45.53−1 min−1, f2 = 26.79−1 min−1 and f3 = 13.11−1 min−1. Although these values are close to those found in this study, they have to be interpreted as no conclusive due to the small length of the time series they used. However, the similitude of their results (obtained from records 30 years apart in time) with those in this study add further robustness to this work.
4. Conclusions
A series of numerical experiments from a barotropic configuration of the GCOM model was conducted to analyze the response to infragravity (IG) waves of the Port of Ensenada, located within Bahia de Todos Santos (BTS), on the west coast of Mexico.
The fundamental oscillation mode of the port was estimated to be T0 = 16.67 min. This value coincided with the third energy peak found at frequency band f0 = 16.66−1 min−1 from spectral estimates of sea level observations inside PE. The remaining two larger period signals were found at frequencies f = 50−1 min−1 and f = 25−1 min−1.
Since the T0 = 16.67 min oscillation wave is the largest wave supported by the EP, larger period energy at bands f = 50−1 min−1 and f = 25−1 min−1 can be considered as generated outside the port. In order to elucidate their source, a simple exercise to estimate the first oscillation modes for the BTS was performed. It gave T0 = 50.48 min, T1 = 25.24 min and T2 = 16.82 min which agreed very well with the values found in the spectral analysis of this study.
Particularly, the wave energy found in the frequency band f0 = 16.66−1 min−1, which comes from the T2 mode of oscillation of the BTS, coincided with the T0 mode of oscillation of the PE; as expected, resonance was found at this frequency (Figure 5 and Figure 7).
Numerical experiments with different frequency forcing presented secondary wave energy peaks at bands f = 8.33−1 min−1 and f = 4.16−1 min−1 which were identified as modes f1 and f2, being f0 = 16.66−1 min−1 the fundamental frequency of the PE. Associated currents (harbor currents) were of the order of 40 - 100 cm∙s−1 in agreement to observations.
The results of this study identified first three BTS oscillation modes as the source of the IG waves recorded at PE; however, in order to be conclusive, more studies are needed.
Finally, local Port Authority is planning to extend the main breakwater of the PE to several hundred meters. The good performance of GCOM makes it an ideal tool to obtain and evaluate the desired information for prospects.
Acknowledgements
Sea level data were kindly provided by Secretaria de Marina (SEMAR, Mexican Navy). Data processing and preliminary spectral analysis were performed by A. Mejia and S. Larios. Computer time was provided by Mexico’s National Oceanographic Data Center, (IIO-UABC).Thanks also go to an anonymous reviewer whose comments helped to improve this paper.