Comparison between Adomian’s Decomposition Method and Toeplitz Matrix Method for Solving Linear Mixed Integral Equation with Hilbert Kernel ()
Received 15 May 2016; accepted 27 June 2016; published 30 June 2016

1. Introduction
The Volterra-Fredholm integral equation (V-FIE) arises from parabolic boundary value problems. The integral equations appear in many problems of physics and engineering. The Adomian decomposition method (ADM) was proposed by George Adomian in [1] [2] . A lot of examination work has been put as of late in applying this method to a wide range of ordinary differential equations, partial differential equations and integral equations, linear and nonlinear. Many authors discussed solutions of linear and nonlinear integral equations by utilizing different methods. What’s more, others interested singular integral equation.
We consider the linear (V-FIE) with singular kernel given by
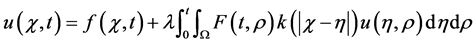 (1)
(1)
There are several techniques that have been utilized to handle the integral Equation (1) in [3] - [5] ; a few techniques, for example, the projection method, time collocation method, the trapezoidal Nystrom method, and furthermore analytical or numerical techniques were utilized to treated this equation, but this techniques experienced troubles as far as computational work utilized. In [6] treated Maleknejad and Hadizadeh Equation (1) by using the Adomian decomposition method presented in [7] [8] introduced Wazwaz [9] the modified Adomian decomposition method for solving the Volterra-Fredholm integral equations.
In this work, we display numerical techniques to obtain numerical solution for linear mixed integral equation with Hilbert kernel. In Section 2, we talk about the existence and uniqueness of the solution. In Section 3, we discuss the Adomian decomposition method, as one of the well known technique and we note that the Adomian polynomials do not appear in this work because we handle linear problems. In Section 4, we present the Laplace Adomian decomposition method and apply this method to linear mixed integral equation with Hilbert kernel. In Sections 5 and 6, we display the Toeplitz matrix method.
2. The Existence and Uniqueness of the Solution [10]
Consider the integral Equation (1), the functions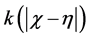 ,
, 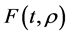 and
and  are given and called the kernel of Fredholm integral term, Volterra integral term and the free term respectively and
are given and called the kernel of Fredholm integral term, Volterra integral term and the free term respectively and  is a real parameter (may be complex and has physical meaning). Also, Ω is the domain of integration with respect to position,
is a real parameter (may be complex and has physical meaning). Also, Ω is the domain of integration with respect to position,
and the time t, . While
. While 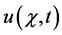 is the unknown function to be determined in the space
is the unknown function to be determined in the space
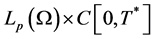 .
.
In order to guarantee the existence of a unique solution of Equation (1) we assume through this work the following conditions:
(i) The kernel of position  ,
,

Satisfies the discontinuity condition

(ii) The kernel of time  satisfies
satisfies ,
, 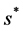 is a constant,
is a constant,
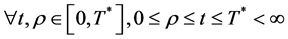 .
.
(iii) The given function ![]() with its partial derivatives with respect to position
with its partial derivatives with respect to position ![]() and time t is conti-
and time t is conti-
nuous in the space![]() , and its norm is defined as
, and its norm is defined as
![]()
(iv) The unknown function ![]() it behaves in this space, as the known function
it behaves in this space, as the known function![]() .
.
3. The Adomian Decomposition Method for Solving Volterra-Fredholm Integral Equation [11] [12]
Adomian decomposition method [1] [2] defines the unknown function ![]() by an infinite series
by an infinite series
![]() (2)
(2)
where the components ![]() will be determined recurrently and the nonlinear term decomposed into an infinite series of Adomian polynomials
will be determined recurrently and the nonlinear term decomposed into an infinite series of Adomian polynomials
![]()
The polynomials ![]() are produced for all kinds of nonlinearity so that
are produced for all kinds of nonlinearity so that ![]() depends just on
depends just on![]() ,
, ![]() relies on upon
relies on upon ![]() and
and![]() , and so on. The Adomian polynomial [1] [2] ,
, and so on. The Adomian polynomial [1] [2] , ![]() , is given by,
, is given by,
![]() (3)
(3)
Substituting Equation (2) into Equation (1) to get
![]() (4)
(4)
The components ![]() are computed using the following recursive relations
are computed using the following recursive relations
![]() (5)
(5)
![]() (6)
(6)
4. The Combined Laplace-Adomian Decomposition Method Applied to Volterra-Fredholm Integral Equation with Hilbert Kernel [13] - [15]
We consider the kernel ![]() of Equation (1) take the form
of Equation (1) take the form ![]() and applying the
and applying the
Laplace transform to both sides of Equation (1) gives:
![]() (7)
(7)
The linear term ![]() will be represented by the Adomian decomposition from Equation (2). Substituting Equation (2) into Equation (7) leads to
will be represented by the Adomian decomposition from Equation (2). Substituting Equation (2) into Equation (7) leads to
![]() (8)
(8)
The Adomian decomposition method introduces the recursive relation
![]()
![]() (9)
(9)
Applying the inverse Laplace transform to the first part of Equation (9) gives![]() . Utilizing
. Utilizing ![]() will empower us to evaluate
will empower us to evaluate![]() , and so on. This will prompt the complete determination of the components of
, and so on. This will prompt the complete determination of the components of ![]() upon utilizing the second part of Equation (9). The series solution follows promptly after utilizing Equation (2). The obtained series solution may converge to an exact solution if such a solution exists.
upon utilizing the second part of Equation (9). The series solution follows promptly after utilizing Equation (2). The obtained series solution may converge to an exact solution if such a solution exists.
5. The System of Fredholm Integral Equations (SFIEs) [16] [17]
In this part, a numerical technique is used, in the integral Equation (1) to obtain a system of linear integral equa-
tions with singular kernel, so we divide the interval![]() ,
, ![]() as
as ![]()
![]() , where
, where ![]() Then the formula (1) reduces to SFIEs of the second kind, in the form:
Then the formula (1) reduces to SFIEs of the second kind, in the form:
![]() (10)
(10)
where
![]()
![]() (11)
(11)
where ![]() is the error.
is the error.
6. The Toeplitz Matrix Method (TMM) [17] - [19]
In this section, we apply (TMM) to obtain the numerical solution of the SFIEs (10) with singular kernel, each equation in this system can be written in a simplify form
![]() (12)
(12)
The integral term in Equation (12) can be written as
![]() (13)
(13)
We approximate the integral in the right hand side of Equation (13) by
![]() (14)
(14)
where ![]() and
and ![]() are two arbitrary functions to be determined and
are two arbitrary functions to be determined and ![]() is the estimate error which depends on
is the estimate error which depends on ![]() and on the way that the coefficients
and on the way that the coefficients ![]() are chosen. Putting
are chosen. Putting ![]() in Equation (14) yields a set of two equations in terms of the two functions
in Equation (14) yields a set of two equations in terms of the two functions ![]() and
and![]() . For choosing the values of
. For choosing the values of![]() , the error
, the error![]() , in this case, must vanish.
, in this case, must vanish.
We can, clearly solve the result set of two equations for ![]() and
and![]() , to obtain
, to obtain
![]() (15)
(15)
![]() (16)
(16)
where
![]()
Hence, Equation (13) takes the form
![]() (17)
(17)
where
![]()
The integral Equation (12), after putting![]() , becomes
, becomes
![]() (18)
(18)
The formula (18) represents a linear system of algebraic equation , where u is a vector of ![]() elements, while
elements, while ![]() is a matrix whose elements are given by
is a matrix whose elements are given by
![]()
![]()
The matrix ![]() is a Toeplitz matrix of order
is a Toeplitz matrix of order![]() , where
, where![]() .
.
The solution of the system (18) can be obtained in the form
![]()
The error term ![]() is determined from Equation (14) by letting
is determined from Equation (14) by letting ![]() , to get
, to get
![]()
7. Numerical Example
Example 1: Consider the linear mixed integral equation with Hilbert kernel
![]() (19)
(19)
![]() , the exact solution
, the exact solution ![]()
we obtain Table 1.
8. Conclusions
In this paper, we applied (LADM) for solution two dimensional linear mixed integral equations of type Volterra- Fredholm with Hilbert kernel. Additionally, comparison was made with Toeplitz matrix method (TMM). It could be concluded that (LADM) was an effective technique and simple in finding very good solutions for these sorts of equations.
Using Maple 18, we obtain Table 1 and Figure 1 (since Figure 1 represents exact solution of u at t = 0.001, λ = 0.01, N = 20).
![]()
Table 1. Results obtained for example 1 and error.
![]()
![]()
Figure 1. The exact value of u and the value of u using (LADM).
Acknowledgements
The authors would like to thank the King Abdulaziz city for science and technology.