Received 18 April 2016; accepted 26 June 2016; published 29 June 2016

1. Introduction
In several papers among them [8] - [11] , integral equations with nonsigular kernels have been studied. In [12] - [14] Darwish et al. introduced and studied the quadratic Volterra equations with supremum. Also, Banaś et al. and Darwish [13] [15] - [17] studied quadratic integral equations of arbitrary orders with singular kernels. In [18] , Darwish generalized and extended Banaś et al. [15] results to the perturbed quadratic integral equations of arbitrary orders with singular kernels.
In this paper, we will study the q-perturbed quadratic integral equation with supremum
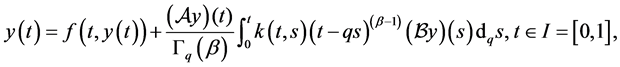 (1)
(1)
where ,
, 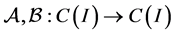 , and
, and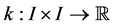 .
.
By using Darbo fixed point theorem and the monotonicity measure of noncompactness due to Banaś and Olszowy [19] , we prove the existence of monotonic solution to Equation (1) in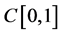 .
.
2. q-Calculus and Measure of Noncompactness
First, for a real parameter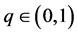 , we define a q-real number
, we define a q-real number 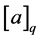 by
by
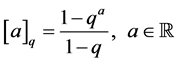 , (2)
, (2)
and a q-analog of the Pochhammer symbol (q-shifted factorial) is defined by
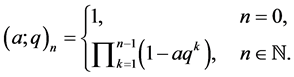 (3)
(3)
Also, the q-analog of the power 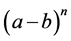 is given by
is given by
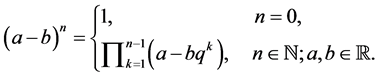 (4)
(4)
Moreover,
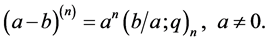 (5)
(5)
Notice that,  exists and we will denote it by
exists and we will denote it by![]() .
.
More generally, for ![]() we define
we define
![]() (6)
(6)
and
![]() (7)
(7)
Notice that![]() . Therefore, if
. Therefore, if![]() , then
, then![]() .
.
The q-gamma function is defined by
![]() (8)
(8)
where ![]() Or, equivalently,
Or, equivalently, ![]() and satisfies
and satisfies ![]()
Next, the q-derivative of a function f is given by
![]() (9)
(9)
and the q-derivative of higher order of a function f is defined by
![]() (10)
(10)
The q-integral of a function f defined on the interval ![]() is defined by
is defined by
![]() (11)
(11)
If f is given on the interval ![]() and
and ![]() then
then
![]() (12)
(12)
The operator ![]() is defined by
is defined by
![]() (13)
(13)
The fundamental theorem of calculus satisfies for ![]() and
and![]() , i.e.,
, i.e.,![]() , and if f is continuous at
, and if f is continuous at![]() , then
, then![]() .
.
The following four formulas will be used later in this paper
![]() (14)
(14)
and
![]() (15)
(15)
where ![]() denotes the q-derivative with respect to variable t.
denotes the q-derivative with respect to variable t.
Notice that, if ![]() and
and![]() , then
, then![]() .
.
Definition 1. [2] Let f be a function defined on![]() . The fractional q-integral of the Riemann-Liouville type of order
. The fractional q-integral of the Riemann-Liouville type of order ![]() is given by
is given by
![]() (16)
(16)
Notice that, for![]() , the above q-integral reduces to (11).
, the above q-integral reduces to (11).
Definition 2. [2] The fractional q-derivative of the Riemann-Liouville type of order ![]() is given by
is given by
![]() (17)
(17)
where ![]() denotes the smallest integer greater than or equal to
denotes the smallest integer greater than or equal to![]() .
.
In q-calculus, the derivative rule for the product of two functions and integration by parts formulas are
![]() (18)
(18)
Lemma 1. Let ![]() and f be a function defined on
and f be a function defined on![]() . Then the following formulas are verified:
. Then the following formulas are verified:
![]() (19)
(19)
Lemma 2. [21] For![]() , using q-integration by parts, we have
, using q-integration by parts, we have
![]() (20)
(20)
or
![]() (21)
(21)
Second, we recall the basic concepts which we need throughout the paper about measure of noncompactness.
We assume that ![]() is a real Banach space with zero element
is a real Banach space with zero element ![]() and we denote by
and we denote by ![]() the closed ball with radius r and centered x, where
the closed ball with radius r and centered x, where![]() .
.
Now, let ![]() and denote by
and denote by ![]() and Conv X the closure and convex closure of X, respectively. Also, the symbols
and Conv X the closure and convex closure of X, respectively. Also, the symbols ![]() and
and ![]() stands for the usual algebraic operators on sets.
stands for the usual algebraic operators on sets.
Moreover, the families ![]() and
and ![]() are defined by
are defined by ![]() and
and ![]() respectively.
respectively.
Definition 3. [22] Let ![]() If the following conditions
If the following conditions
1)![]() .
.
2) ![]()
3) ![]()
4) ![]() and
and
5) if ![]() is a sequence of closed subsets of
is a sequence of closed subsets of ![]() with
with ![]() and
and ![]()
then ![]() hold. Then, the mapping
hold. Then, the mapping ![]() is said to be a measure of noncompactness in E.
is said to be a measure of noncompactness in E.
Here, ![]() is the kernel of the measure of noncompactness
is the kernel of the measure of noncompactness![]() .
.
Our result will establish in C(I) the Banach space of all defined, continuous and real functions on ![]() with
with![]() .
.
Next, we defined the measure of noncompactness related to monotonicity in![]() , see [19] [22] .
, see [19] [22] .
We fix a bounded subset ![]() of
of![]() . For
. For ![]() and
and ![]() denotes the modulus of continuity of the function y given by
denotes the modulus of continuity of the function y given by
![]() . (22)
. (22)
Moreover, we let
![]() (23)
(23)
and
![]() (24)
(24)
Define
![]() (25)
(25)
and
![]() (26)
(26)
Notice that, all functions in Y are nondecreasing on I if and only if![]() .
.
Now, we define the map ![]() on
on ![]() as
as
![]() (27)
(27)
Clearly, μ verifies all conditions in Definition 3 and, therefore it is a measure of noncompactness in ![]() [19] .
[19] .
Definition 4.Let ![]() Let
Let ![]() be a continuous operator. Suppose that
be a continuous operator. Suppose that ![]() maps bounded sets onto bounded ones. If there exists a bounded
maps bounded sets onto bounded ones. If there exists a bounded ![]() with
with![]() , then
, then ![]() is said to be satisfies the Darbo condition with respect to a measure of noncompactness
is said to be satisfies the Darbo condition with respect to a measure of noncompactness![]() .
.
If![]() , then
, then ![]() is called a contraction operator with respect to
is called a contraction operator with respect to![]() .
.
Theorem 1. [23] Let ![]() be a bounded, convex and closed subset of E. If
be a bounded, convex and closed subset of E. If ![]() is a Contraction operator with respect to
is a Contraction operator with respect to![]() . Then
. Then ![]() has at least one fixed point belongs to Q.
has at least one fixed point belongs to Q.
3. Existence Theorem
Let us consider the following suggestions:
a1) ![]() is continuous and
is continuous and
![]()
Moreover, ![]() and
and ![]()
a2) The superposition operator F generated by the function f satisfies for any nonnegative function y the condition![]() , where c is the same constant as in a1).
, where c is the same constant as in a1).
a3) ![]() is a continuous operator which satisfies the Darbo condition for the measure of noncompactness
is a continuous operator which satisfies the Darbo condition for the measure of noncompactness ![]() with a constant
with a constant![]() . Also,
. Also, ![]() if
if![]() .
.
a4)![]() .
.
a5) The function ![]() is continuous on
is continuous on ![]() and nondecreasing
and nondecreasing ![]() and separately. Moreo-
and separately. Moreo-
ver, ![]()
a6) ![]() is a continuous operator and there is a nondecreasing function
is a continuous operator and there is a nondecreasing function ![]() such that
such that ![]() for any
for any![]() . Moreover, for every function
. Moreover, for every function ![]() which is nonnegative on I, the function
which is nonnegative on I, the function ![]() is nonnegative and nondecreasing on I.
is nonnegative and nondecreasing on I.
a7) ![]() such that
such that
![]() (28)
(28)
and![]() .
.
Before, we state and prove our main theorem, we define the two operators ![]() and
and ![]() on
on ![]() as follows
as follows
![]() (29)
(29)
and
![]() (30)
(30)
respectively. Finding a fixed point of the operator ![]() defined on the space
defined on the space ![]() is equivalent to solving Equation (1).
is equivalent to solving Equation (1).
Theorem 2. Assume the suggestions (a1)-(a7) be verified, then Equation (1) has at least one solution ![]() which is nondecreasing on I.
which is nondecreasing on I.
Proof. We divide the proof into seven steps for better readability.
Step 1: We will show that the operator ![]() maps
maps ![]() into itself.
into itself.
For this, it is sufficient to show that ![]() if
if![]() . Fix
. Fix ![]() and let
and let ![]() and
and ![]() with
with![]() . We have
. We have
![]() (31)
(31)
Notice that, we have used
![]() (32)
(32)
Notice that, since the function k is uniformly continuous on![]() , then when
, then when ![]() we have that
we have that![]() .
.
Thus![]() , and therefore,
, and therefore, ![]()
Step 2: ![]() applies
applies ![]() into itself.
into itself.
Now, ![]() , we have
, we have
![]() (33)
(33)
Hence
![]() (34)
(34)
Therefore, if ![]() we get from assumption a7) the following
we get from assumption a7) the following
![]() (35)
(35)
Therefore, ![]() maps
maps ![]() into itself.
into itself.
We define the subset ![]() of
of ![]() by
by
![]() (36)
(36)
It is clear that ![]() is closed, convex and bounded.
is closed, convex and bounded.
Step 3: ![]() applies the set
applies the set ![]() into itself.
into itself.
By this facts and suggestions a1), a4) and a6), we obtain ![]() transforms
transforms ![]() into itself.
into itself.
Step 4: The operator ![]() is continuous on
is continuous on![]() .
.
To prove this, we fix ![]() to be a sequence in
to be a sequence in ![]() with
with![]() . We will show that
. We will show that![]() .
.
Thus, we have![]() ,
,
![]() (37)
(37)
Consequently,
![]() (38)
(38)
As ![]() and
and ![]() are continuous operators,
are continuous operators, ![]() such that
such that
![]() (39)
(39)
Also, ![]() such that
such that
![]() (40)
(40)
Furthermore, ![]() such that
such that
![]() (41)
(41)
Now, take![]() , then (38) gives us that
, then (38) gives us that
![]() . (42)
. (42)
This shows that ![]() is continuous in
is continuous in![]() .
.
Step 5: In recognition of ![]() with respect to the quantity
with respect to the quantity![]() .
.
Now, we take ![]() Let us fix an arbitrarily number
Let us fix an arbitrarily number ![]() and choose
and choose ![]() and
and ![]() with
with![]() . We will be supposed that
. We will be supposed that ![]() because no generality will be loss. Then, by using our suggestions and inequality (31), we get
because no generality will be loss. Then, by using our suggestions and inequality (31), we get
![]() (43)
(43)
The last estimate implies
![]() (44)
(44)
and, consequently,
![]() (45)
(45)
Since the function k is uniformly continuous on ![]() and the function f is continuous on
and the function f is continuous on![]() , then the last inequality gives us that
, then the last inequality gives us that
![]() (46)
(46)
Step 6: In recognition of ![]() with respect to the quantity d.
with respect to the quantity d.
Here, we fix an arbitrary ![]() and
and ![]() with
with![]() . Then, by our assumption, we obtain our suggestions, we have
. Then, by our assumption, we obtain our suggestions, we have
![]() (47)
(47)
Now, we will prove that
![]() (48)
(48)
We find that
![]() (49)
(49)
But, ![]() because
because ![]() is increasing with respect to t, then
is increasing with respect to t, then
![]() (50)
(50)
and, since ![]() is negative for
is negative for ![]() then
then
![]() (51)
(51)
Inequalities (50) and (51) imply that
![]()
This inequality and (47) gives us
![]() (52)
(52)
The above estimate implies that
![]() (53)
(53)
Therefore,
![]() (54)
(54)
Step 7: ![]() is contraction with respect to the measure of noncompactness
is contraction with respect to the measure of noncompactness![]() .
.
Inequalities (46) and (54) give us that
![]() (55)
(55)
or
![]() (56)
(56)
But![]() , then
, then
![]() (57)
(57)
Inequality (57) enables us to use Theorem 1, then there are solutions to Equation (1) in![]() .
.
This finishes our proof.