Received 28 April 2016; accepted 16 June 2016; published 21 June 2016
1. Introduction
In his pioneering studies of the harmonic oscillator Planck [1] showed that there existed a lowest nonzero ground state energy level, now called Zero Point Energy (ZPE). An example of the related electromagnetic vacuum fluctuations was later given by Casimir [2] who predicted that two metal plates would attract each other when being sufficiently close together. This force was first confirmed experimentally by Lamoreaux [3] . It reveals the existence of a real macroscopic pressure and energy density, originating from photon-like fluctuations of the ZPE. Consequently the vacuum is not a state of empty space.
The low-frequency part of the ZPE fluctuations has to be accepted as an experimental fact, but a problem arises with its high-frequency part. The earlier performed conventional analysis leads namely to a spectrum having an infinite total energy density, as demonstrated by Terletskii [4] , Milonni [5] and Loudon [6] among others. As pointed out by the author [7] - [11] , this is unacceptable from the physical point of view, as well as due to the facts that such an analysis both becomes underdetermined and is based on states of the ensemble which all have the equal probabilities of unity. Also Riess and Turner [12] and Heitler [13] have thrown doubts upon this conventional theory on the ZPE spectrum.
To overcome this difficulty, the author [9] - [11] has proposed the ensemble of ZPE modes to be treated separately, on the condition of a finite integrated total energy, and being relevant also at the temperature
. This has been done in the standard way of considering oscillations of frequency 
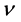populating the available states of an ensemble in statistical equilibrium, i.e. with a probability equal to a Boltzmann factor
.
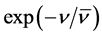Here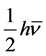 
is the average and finite member energy of these states, having the corresponding average fre-
quency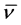
. This leads to a physically acceptable, self-consistent and finite total pressure of the ZPE “photons”.
The purpose of the complementary investigations presented in this paper is twofold. First, the theory of the ZPE spectrum will be used in models on dark matter and dark energy, applied both to the observable universe considered as an entity, and to galaxies including supermassive black holes at their centra. Second, an ex- perimental determination is desirable which aims at the so far unknown value of the average frequency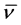 
of the ZPE spectrum, measured at the position of the Earth. As to be shown here, this can possibly be realized by means of measurements on the maximum available Casimir force acting on metals of different electromagnetic skin depths.
2. Theory on the Zero Point Energy
2.1. The ZPE Spectrum
In the present revised theory on the ZPE spectrum [8] - [10] , the contribution to the local energy density u in the spectral range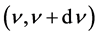 
becomes
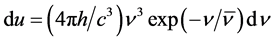(1)
This results in a finite integrated energy density
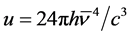(2)
where the average frequency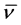 
is unknown so far.
2.2. An Interpretation of Dark Matter and Dark Energy
The self-consistent spectrum of Equations (1) and (2) has been proposed as the basis for a new interpretation of dark matter and dark energy [8] [9] . The corresponding analysis is here limited to an isotropic pressure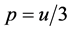 
in spherically symmetric geometry. With the radial coordinate r, a local expansive force density in the outward direction arises from the pressure gradient, as given by
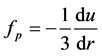(3)
This represents the local contribution to dark energy.
The integrated relativistic mass due to ZPE further becomes
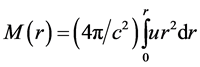(4)
as being contained within a sphere of radius r. Here cases will also be considered where there exists a super- massive black hole of mass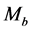 
at the centre
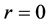. The total local contracting gravitational force density in the negative radial direction then becomes
![]()
(5)
where ![]()
is the constant of gravitation. This force density thus represents the total and local contribution to dark matter. Two cases will be considered here. The first concerns a local balance of the forces in absence of a black hole mass![]()
. Then an exact solution can be found. The second case includes the mass ![]()
and where only a solution for an average balance so far becomes available.
2.2.1. Local Balance
A local balance between the expansive and contracting forces is given by![]()
, leading to
![]()
(6)
So far local forms of ![]()
have not been found which satisfy this equation when![]()
.
In the case![]()
, a local solution of the form ![]()
is on the other hand available [8] . It results in the relations
![]()
(7)
and
![]()
(8)
2.2.2. Average Balance
The condition of an average balance can still be obtained by substituting ![]()
by a mean value![]()
. This value then prevails within a spherical volume of radius R, with ![]()
at points![]()
. The local ex- pansive force of Equation (3) is then replaced by an integrated total pressure force
![]()
(9)
at the boundary![]()
. Integrating the gravitational force (5) over the total volume further yields a total con- tracting force
![]()
(10)
The condition ![]()
of average balance then leads to
![]()
(11)
having a maximum
![]()
(12)
at ![]()
where ![]()
and![]()
. At this maximum the total ZPE mass becomes
![]()
(13)
The energy density (11) has the following properties as a function of R:
・ A balance is only possible for ![]()
because ![]()
and ![]()
are by definition positive, as well as the mean energy density![]()
.
・ The density ![]()
increases from zero at![]()
, to the maximum ![]()
at![]()
. This relatively large value of![]()
, and the related ZPE mass (13), can be considered as the result of a reinforcement of dark matter by the black hole mass, in the case of an existing equilibrium.
・ For values![]()
, ![]()
further decreases and approaches the form ![]()
at large R where ![]()
becomes independent of the black hole mass![]()
.
2.3. Cosmical Applications
The present theoretical concepts and interpretations can here be applied to two examples:
・ The observable universe considered as an entity, with mean properties at its largest scale corresponding to an averaged ZPE energy density.
・ Subregions of the universe, on a smaller scale such as that of the galaxies within which there can exist gravitationally contracted local parts of higher ZPE energy density.
2.3.1. The Observable Universe
The radius of the observable universe is estimated to about 1026 m by astronomers. In its present stage of expansion it contains about 4% of normal matter, about 23% of dark matter, and about 73% of dark energy as given by Linder and Permutter [14] and Perlmutter [15] . This state thus deviates to a certain extent from an equilibrium. The normal matter has thereby an average density of about 10−26 kg∙m−3 according to Linde [16] . The estimated ZPE energy density then becomes about![]()
.
Turning first to the imagined case of local balance between dark matter and dark energy in absence of normal matter, this leads to Equations (6)-(8) for![]()
. Equation (8) then results in an average energy density
![]()
(14)
in local equilibrium. With the radius R in the range from ![]()
to ![]()
m, this would result in an energy density ranging from ![]()
to ![]()
J∙m−3, respectively.
We next consider the present state of a certain deviation from equilibrium. As an approximation, the average density ![]()
is then determined from expressions (9) and (10) with ![]()
and under the condition ![]()
. It results in
![]()
(15)
With R in the range from ![]()
to ![]()
m this corresponds to an average density in the range from ![]()
to ![]()
J∙m−3, respectively. The density obtained from Equation (15) is thus within the same range as the estimated one. This can be taken as a support of the present theory.
2.3.2. The Milky Way
As subregion we now take the Milky Way as an example, having a radius of about ![]()
m and a thickness of about ![]()
m. According to Ghez et al. [17] there is a supermassive black hole at its centre, with a mass of about ![]()
kg, i.e. ![]()
solar masses. Its volume is reduced to 10−7 of the solar volume, corre- sponding to a radius of about ![]()
m.
Turning to the average balance of Equations (9)-(13), we notice the following results obtained with ![]()
and![]()
:
・ In the balance between the expansive and contracting forces, relation (11) permits several possible values of![]()
. This introduces some uncertainty in the interpretation. It may also not become necessary to satisfy the balance condition exactly, in analogy with the case of Equation (15) of the universe as an entity.
・ There is a smallest possible radius equal to![]()
.
・ The maximum of ![]()
occurs at ![]()
which is much larger than the radial extension of the supermassive black hole. It leads to![]()
. This is an extremely high value, corresponding to a total ZPE mass ![]()
of Equation (15). It might be realized only under special con- ditions.
・ The branch of Equation (11) at large ![]()
is almost independent of![]()
, and it leads to the limit![]()
. Choosing a radius of the order of the thickness of the Milky Way, and which roughly corresponds to the position of the Earth within it, this results in a local density of about![]()
. This density value is substantially higher than the average ZPE energy density of the universe considered as an entity.
3. Experimental Determination of the Dark Energy Density
There is no exact theoretical indication so far about the magnitude of the dark ZPE energy density at the position of the Earth’s orbit. Here a possible experimental procedure will be presented for determination of it.
3.1. The Casimir Force
The first investigations on the Casimir force were performed on a small but nonzero air gap between two metal plates. The largest available force of this kind would on the other hand arise in the case of a vanishing air gap [10] . Then the electromagnetic skin depths of the plates will play the rôle of an equivalent gap.
Starting from the spectrum of Equations (1) and (2), the Casimir force arises from the difference in pressure on the in- and outsides of the metal plates. Whereas the full ZPE pressure acts on their outsides, there is a reduced pressure on their insides due to the boundary condition which sorts out all frequencies below a certain limit![]()
. The latter corresponds to wavelengths larger than![]()
. The net Casimir pressure thus becomes
![]()
(16)
Normalizing by the introduction of ![]()
and![]()
, we obtain
![]()
(17)
where
![]()
(18)
and
![]()
(19)
3.1.1. Results from a Nonzero Air Gap
We first consider the case of a nonzero air gap of the width d, being much larger than the electromagnetic skin depth of the plates at relevant frequencies. Then frequencies lower than ![]()
and wavelengths larger than ![]()
will be excluded. In the limit![]()
, the function ![]()
approaches the value![]()
, corresponding to a net pressure
![]()
(20)
as shown by Casimir [2] and being applicable to earlier experiments. The result (20) only involves the low- frequency part of the spectrum. It therefore indicates that the full Casimir force should become substantially larger at ever decreasing gap widths, up to a certain limit which includes the entire ZPE spectrum. Thus the pressure (20) is independent of the average frequency ![]()
of Equation (1), and it appears first in the total pressure (18).
3.1.2. Results from a Vanishing Air Gap
We next turn to the maximum Casimir force of a vanishing air gap. Then the width d is replaced by the sum of the skin depths ![]()
and ![]()
of two plates (1) and (2) consisting of different metals, the choice of which will be described later. This leads to a total skin depth
![]()
(21)
where the effective electrical conductivity becomes
![]()
(22)
with ![]()
and ![]()
standing for the electrical conductivities of each metal. In the limit where half a wavelength ![]()
is equal to the total skin depth (21), the corresponding frequency limit becomes
![]()
(23)
Since ![]()
varies as ![]()
and ![]()
as![]()
, all frequencies ![]()
less than ![]()
are excluded by the boundary condition. Therefore ![]()
represents the Casimir frequency limit, as in the analogous case of a nonzero air gap.
We now consider a given total energy density u and a total pressure ![]()
expressed by Equation (18), with ![]()
and ![]()
given by Equations (17) and (19), and ![]()
by Equation (23). The Casimir pressure ![]()
then becomes a function of the average frequency ![]()
for a given effective conductivity (22). This dependence is shown in Figure 1 for the combinations Ag/Cu, Al/Cr, Ni/Cd, Ta/Pb and Sb/Bi of plate pairs:
・ The left-hand part of the figure relates to large values of ![]()
for which ![]()
already includes the full pressure![]()
, and for which there is a vanishing difference between the various plate combinations.
・ The right-hand part of the same figure corresponds on the other hand to small ![]()
for which there is a difference due to the various effective resistivities. This part leads to a pressure ![]()
having the asymptotic limit
![]()
(24)
due to Equations (17)-(19), where the frequency limit ![]()
is given by Equation (23). Thus the limit![]()
, be- comes independent of the average frequency![]()
, but depends strongly on the choice of plate material.
3.2. Proposed Experimental Investigations
A vanishing air gap has the advantage of a maximum Casimir force. The latter may even become recordable by means of a simple lever balance. This is gained at the expense of the following questions:
・ To avoid effects from the air pressure, the measurements should take place in vacuo.
・ To avoid microscopic matching between the metal structures, plate pairs of different metals should be chosen, as pointed out by Abramson [18] and Brodin [19] . Metals with any form of ferro magnetism should also be excluded.
・ Even with a maximum Casimir force, other surface and sticking mechanisms may interfere with the measurements, such as the Van der Waals forces. To minimize this problem, many independent measure- ments with various plate combinations have to be made, to sort out the special behaviour on the skin depths represented by Figure 1.
3.2.1. Estimations from Existing Data
The possible relation between the Casimir force and the magnitude of the ZPE energy density at the orbit of the Earth, can be used in first estimations of this density:
・ From the results of the previous Section 2.3.2, the density ![]()
at the Earth’s orbit has roughly been estimated to give rise to a total pressure![]()
. In Figure 1 this would correspond to a parameter range around ![]()
and![]()
.
・ In earlier experiments with an air gap as small as![]()
, the net Casimir pressure (20) becomes![]()
. With air gaps of this magnitude, the pressure ![]()
is then expected to be much smaller than the pressure ![]()
of the total spectrum. Due to Figure 1 this then implies that ![]()
should in any case be larger than 1014 s−1.
3.2.2. Experiments on the Maximum Casimir Force
A detailed research on the total ZPE energy density in the laboratory is proposed here, and may be performed in a series of measurements of the Casimir pressure ![]()
with various plate combinations. With these values of ![]()
introduced into Figure 1, corresponding values of the average frequency would be found, as predicted by the theory. This leads to the following situation:
・ If all obtained values of ![]()
point to the same value of ![]()
then the latter is with high probability to be identified as the average frequency of the ZPE spectrum of Equation (1).
・ If the measured values of ![]()
would on the other hand point to different values of![]()
, the measured result is likely to be disturbed by other unknown effects.
4. Conclusions
The frequency spectrum of the zero Point Energy and its total density on cosmical scale are unknown in their details. The present complementary investigation includes a revised theory, forming the basis for determinations of this energy density. First, this concerns the values of the latter within the observable universe considered as an entity, as well as in subregions such as the galaxies including supermassive black holes. Second, experiments are proposed on the maximum Casimir force between metal plates with vanishing gap distance, with the purpose of determining the ZPE energy density in the laboratory, i.e. at the orbit of the Earth. These problems thus concern the ZPE on cosmical scale, with its interaction with gravity.
In the present approach the ZPE energy density is interpreted as a dark matter density, and its pressure gradient as a dark energy force density. The lack of emitted radiation is reconcilable with this picture. Thereby the crucial coincidence problem of equal orders of magnitude of dark matter and dark energy cannot be ex- plained by the cosmological constant. This problem is instead resolved by the present variable concepts originating from the same ZPE photon gas balance.
An additional and different effect due to ZPE arises on the microscopical scale of elementary particles, as explained earlier by the author [20] [21] . This concerns the ZPE connection with the particle rest masses, as obtained from a nonzero divergence of the electric field strength in vacuo. It leads among other things to a composite boson, having the same basic properties and mass as the 125 GeV particle detected by CERN, but with no relation to the theory by Higgs.