

1. Introduction
In recent years, wireless broadband access technologies have been developed rapidly. IEEE 802.16d/e [1] [2], known as WiMAX, is a wireless broadband standard which attracts more attention. Comparing with other wireless technologies, it has advantages of high bandwidth and Quality of Service (QoS) guarantee features. These standards define the framework of WiMAX QoS guarantee, but the radio resource management algorithms are not given in detail, as they are left for equipment manufacturers to design. However, Call Admission Control (CAC) technologies are essential to guarantee the users QoS requirements, as they control the congestion, while achieving the system efficiency by optimizing the network resources. Therefore, in WiMAX networks it is a key point to design an efficient CAC algorithm.
CAC is a mechanism to keep a reasonable balance between user QoS guarantee and utilization of network resources, the purpose of which is to decide, at the arrival time of a call, whether or not it should be admitted into the network: a new call is admitted if and only if its QoS constraints can be satisfied without jeopardizing the constraints of existing calls in the network. Thus, parameters and the algorithm for estimating the network traffic and the strategy of CAC decision are key point of CAC. At present, most proposed CAC technologies for WiMAX networks [3]-[10] use the classical Poisson process to describe the network traffic and focus on the design and optimization of decision strategy. While they ignored the effect that the network traffic model has a great impact on CAC decision. In fact, the Poisson process can not precisely describe the Internet traffic behaviour. Leland [11] et al. clearly proposed the existence of self-similar of network traffic in the early 1990s firstly. Cristina [12] and Dedi [13] et al. analysed and evaluated that WiMAX traffics are with self-similarity and long range dependent features. So, if the Poisson process is still used to describe the WiMAX traffic, there must be a certain gap between the actually used bandwidth and the predicted traffic. Allocating network resources by the classic predicted traffic model will result in a waste of network resources.
According to the self-similarity of WiMAX network traffic, this paper proposes a novel WiMAX network traffic model based on the M/Pareto model to describe the different levels of the WiMAX network traffic, and derives a formula for calculating the effective bandwidth of the network traffic. Accordingly, we also, propose a modified self-similar call admission control algorithm (SS-CAC). Analysis and simulation results show that our traffic model is more accurate to describe the characteristics of network traffic than the Poisson model, and SS-CAC effectively saves bandwidth and improves the utilization of network resources.
The rest of the paper is organized as follows: Section II introduces the self-similarity theoretical basis, the M/Pareto model describing the burst traffic of many ON/OFF sources and the FBM model for self-similar traffic prediction; Section III presents a model for calculating the effective bandwidth of WiMAX network traffics; Section IV presents the modified self-similar admission control algorithm; Section V explores the simulation results and the analysis; Section VI concludes the work presented in this paper and highlights the recommendation for the future work.
2. Theoretical Basis
2.1. Self-Similar
In the following, by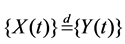 , we denote equality of all joint distributions for Rd-valued stochastic processes
, we denote equality of all joint distributions for Rd-valued stochastic processes  and
and 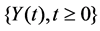 defined on some probability space {W,F,R}. We also simply write
defined on some probability space {W,F,R}. We also simply write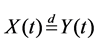 .
.
Definition 1. An Rd-valued stochastic processes 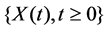 is said to be self-similar with exponent H > 0 if for any a > 0 such that
is said to be self-similar with exponent H > 0 if for any a > 0 such that
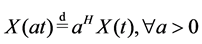 . (1)
. (1)
We call H the exponent of self-similarity of the process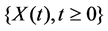 . We refer to such a process as H-self- similar (or H-ss, for short).
. We refer to such a process as H-self- similar (or H-ss, for short).
Let 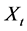 with
with 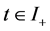 be a covariance stationary stochastic process with mean
be a covariance stationary stochastic process with mean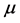 , variance
, variance 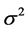 and autocorrelation function
and autocorrelation function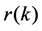 . In particular, we assume
. In particular, we assume
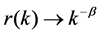 as
as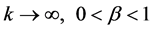 .
.
Definition 2 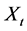 is exactly second-order self-similar with parameter
is exactly second-order self-similar with parameter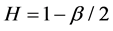 , if for all
, if for all ![]() and
and ![]()
![]() ,
,
where ![]() is the autocorrelation function of
is the autocorrelation function of![]() .
. ![]() is defined as
is defined as![]() .
.
Definition 3 ![]() is asymptotically second-order self-similar with parameter
is asymptotically second-order self-similar with parameter![]() , if for all
, if for all ![]()
![]() .
.
2.2. Self-Similarity of M/Pareto Model
M/Pareto [14] burst traffic is regarded as a superposition of many ON/OFF sources with heavy tailed ON or OFF durations. These bursts arrives by the Poisson process with the arriving rate λ, and the duration of each burst is a random variable X, which follows Pareto distribution with the shape parameter α and position parameter δ (δ for burst shortest duration). Thus, the complementary distribution function can be expressed as
![]() . (2)
. (2)
Expectation of the random variable X is given by![]() , and the variance is infinite (that does not exist).
, and the variance is infinite (that does not exist).
Assuming all burst data packets transmission rate r is same, the mean burst size is expressed as![]() , and the expectation of the total number of packets which are transferred in an interval t can be obtained by
, and the expectation of the total number of packets which are transferred in an interval t can be obtained by![]() .
.
The variance of Pareto distribution is infinite, but the variance of the M/Pareto process is finite, the repeated integral form of which variance function is as follow
![]() . (3)
. (3)
Repeated integration leads to following expression:
![]() . (4)
. (4)
If Hurst parameter is H = (3 − α)/2, approximate variance is proportional to t2H with the growth of t, i.e.:
![]() . (5)
. (5)
Therefore, the process is an asymptotic self-similar process with Hurst parameter H:
![]() . (6)
. (6)
The average rate for the aggregate traffics is
![]() . (7)
. (7)
Then, by the formula (5) and (7) we can be deduced:
![]() . (8)
. (8)
2.3. FBM Model for Self-Similar Traffics Prediction
Firstly we define normalised fractional Brownian motion (BFM) Z(t) with self-similar parameter H (![]() ), in other word, Z(t) is mainly characterised by zero mean and variance t2H for t > 0. Then, self- similar traffic model A(t) based on the fractional Brownian motion is given in [15] by Z(t), A(t) is defined as follows:
), in other word, Z(t) is mainly characterised by zero mean and variance t2H for t > 0. Then, self- similar traffic model A(t) based on the fractional Brownian motion is given in [15] by Z(t), A(t) is defined as follows:
![]() , (9)
, (9)
where A(t) is the total amount of the traffic until the time t, which is described by three parameters: m, a, H. The average transmission rate is given by m > 0, a > 0 denotes the variance coefficient, and H represents the self-similarity parameter (Hurst parameter) of Z(t). Accordingly, the relationship between them is
![]() , (10)
, (10)
where σ2 is the variance of the traffic within one unit time. Then fractional Brownian cache process X(t) is a stochastic process, namely:
![]() , (11)
, (11)
where constant C represents service rate (that is, the link capacity), A(t) denotes the FBM traffic model. Consequently Norros deduce the effective bandwidth formula with cache capacity by fractional Brownian storage process X(t):
![]() , (12)
, (12)
where![]() , variable m and a represent the average transmission rate (in bits/sec) of the traffic and the variance coefficient of the traffic (in bit-sec), respectively. Constant H, ε, and x denote the self-simi- lar Hurst parameter (
, variable m and a represent the average transmission rate (in bits/sec) of the traffic and the variance coefficient of the traffic (in bit-sec), respectively. Constant H, ε, and x denote the self-simi- lar Hurst parameter (![]() ), the packet loss rate, and the cache capacity (in bit), respectively. It is worth noting that the derivation of this formula is based on two premises: firstly, the traffic follows Gaussian distribution. Secondly, cache capacity must be large enough. They are described in [16] in details. Therefore, these two conditions must be ensured in the application, or will not we get the desired results.
), the packet loss rate, and the cache capacity (in bit), respectively. It is worth noting that the derivation of this formula is based on two premises: firstly, the traffic follows Gaussian distribution. Secondly, cache capacity must be large enough. They are described in [16] in details. Therefore, these two conditions must be ensured in the application, or will not we get the desired results.
Section II-B and Section II-C describe that cumulative traffic of the M/Pareto process is fractional Gaussian processes, then the properties of the cumulative traffic are the same with A(t). If the two models describe the same accumulative fractional arrival process, they have the same statistical properties and self-similarity. Therefore, their expectation and variance values are corresponding equal, and so does self-similar parameter H. Thus, the variance of A(t) is expressed as
![]() . (13)
. (13)
Above all, by the formula (8) and formula (13) we can obtain variance coefficient a,
![]() . (14)
. (14)
3. Traffic Model in WiMAX
3.1. Main Idea of WiMAX Traffic Modelling
The literature [17] proved that M/Pareto model can be seen as a large number of independent ON/OFF model with heavy-tailed distribution, and the ON/OFF model with the following characteristics can be convenient to describe the real network traffic.
Firstly, a single traffic contains random data packet bursts, and the length of the bursts follows the heavy- tailed distribution, decay rate obeys the Pareto distribution, after the completion of the burst generated, a silent period of random time is maintained.
Secondly, the number N of the single traffic is large enough to be regarded as infinite, but the data source with the arrival rate λ is finite.
Finally, the aggregated traffic is an asymptotic self-similar process with Hurst parameter H (![]() ).
).
As mentioned earlier, the WiMAX traffic has the characteristics of self-similarity and long-range dependence, and a single traffic in WiMAX is in line with the above characteristics, so we model this single traffic by the ON/OFF model, and the appropriate parameters are determined by each type of traffic descriptors (the peak rate as PR, the average rate as SR).
3.2. Traffic Modelling
In WiMAX system IEEE 802.16d/e standard support the five kinds of traffics: Unsolicited Grant Service (UGS), real-time Polling Service (rtPS), extended real-time Polling Service (ertPS), non-real-time Polling Service (nrtPS), and Best Effort (BE).
The UGS real-time traffic source transmits a fixed length packet at the fixed bit-rate in periodic time intervals. Assuming the data transmission rate of a fixed-size packet is rUGS, then the peak rate of the UGS traffic is PR1 = rUGS, and the mean rate is SR1 = rUGS.
The rtPS real-time traffic source transmits variable-length packets at variable bit rate. If the maximum value of the variable bit rate is rrtps-max, and minimum is rrtps-min, the peak rate of the rtPS traffic is PR2 = rrtps-max, and the mean rate is SR2 = (rrtps-max + rrtps-min)/2.
The nrtPS non-real-time traffic source transmits variable-length packets at variable bit rate. If the maximum value of the variable bit rate is rnrtps-max, and minimum is rnrtps-min, the peak rate of the nrtPS traffic is PR3 = rnrtps-max, and mean rate is SR3 = (rnrtps-max + rnrtps-min)/2.
The BE non-real-time traffic source has no requirement of delay jitter and transmission rate, but in the system for each traffic the maximum transmission rate is a certain limit. If the maximum bit transmission rate is rbe-max, and minimum is rbe-min = 0, the peak rate of BE traffic is PR4 = rbe-max, and mean rate is SR4 = (rbe-max + rbe-min)/2.
The ertPS real-time traffic source transmits variable-length packets at variable rate, but allocates bandwidth like UGS, added by 802.16e. If the maximum value of the variable bit rate is rertps-max, and minimum is rertps-min, the peak rate of the ertPS traffic is PR5 = rertps-max, and mean rate is SR5 = (rertps-max + rertps-min)/2.
3.3. ON/OFF Model of Superposition Traffics
In WiMAX networks traffics are made up of the five types of traffics above description, it is assumed that these five kinds of traffic burst durations follow the same Pareto distribution with shape parameter α, position parameters δ. The number N of the traffic sources is so large that the aggregation of these traffics follows M/ Pareto model with arriving rate![]() .
.
Each type of traffic descriptor is {PRi, SRi}, the activity probability of which can obtained by descriptor parameters:
![]() . (15)
. (15)
As a result, the average rate of the aggregation traffic can be obtained by the activity probability of each type of traffic flow:
![]() , (16)
, (16)
where M represents the number of traffic types, λi denotes the activity number of the i-th traffic, ![]() , Ni indicates the present number of the i-th connections, PRi represents the peak rate of the i-th traffic, δij repre-
, Ni indicates the present number of the i-th connections, PRi represents the peak rate of the i-th traffic, δij repre-
sents a new reach of the j-th traffic![]() .
.
4. Self-Similar Call Admission Control Alg
4.1. Main Idea
By collecting burst duration data in WiMAX system, the moment estimation or maximum likelihood estimation method is used to determine the parameters α, δ of Pareto distribution in the M/Pareto model, and each burst at the ON period sends data at the maximum rate PRi, and the connection number of each type of traffic is Ni at each moment. By the traffic descriptor {PRi, SRi}, the probability of the traffic can be calculated at the ON period, so the activity number of the traffic λi can be obtained by the binomial distribution, and the average transmission rate m of the aggregate traffic can be get in the system.
Corresponding traffic descriptor {PRj, SRj} are substituted into the formula (16) after the arrival of a new traffic j, then the average transmission rate m of the aggregate traffics can be calculated. If corresponding parameters on formula (14) are known, you will get variance coefficient a. Therefore, by M/Pareto model you determine out a FBM model parameters (m, a, H), then making use of the calculation formula (12) the effective bandwidth c of aggregate traffic can be estimated. If c is greater than the available bandwidth C of the system (i.e. c > C), the traffic is rejected, or not to be accepted.
4.2. Implementation
The specific algorithm of SS-CAC is described as follows:
Input: (PRj, SRj, j)
Input parameter j represents the current request of the j-th traffic, and PRj and SRj denote the peak rate of the traffic and the average rate of the traffic, respectively.
Output: CAC decision-making
Decision value is a logical value, and TRUE represents that the request of the traffic is accepted, on the contrary, FALSE shows that the request of the traffic is rejected.
Parameters α, δ denote shape and position parameter of Pareto distribution, respectively, and parameter ε, x and C represent packet loss rate, buffer capacity and the bandwidth available in the system, respectively.
5. Simulation and Analysis of Alg
5.1. Set up Simulation Parameters
SS-CAC algorithm simulation is implemented in NS2. The ON/OFF model is used to simulate traffic source, and traffic source with arrival rate λ sends data at peak rate at the ON period, and ON period follows Pareto distribution. On the other hand, at the OFF period data is not sent, OFF period follows Poisson distribution, and ON and OFF periods alternate. In the simulation, we set the average time of the ON period and OFF period in the ON/OFF model to 500 ms, and the ON period follows Pareto distribution with shape parameter α = 1.4, the transmission rate of the bursts is 6.4 kbps, the size of each packet is 200B, all types of parameters are summarized in Table 1.
The network topology of simulation is PMP mode, and the specific is shown in Figure 1. Each subscriber station SSi transmits data packets to the base station BS, meanwhile, the base station BS receives data packets and forwards them. In the simulation, we set the bandwidth of the base station BS to 128 kbps, cache size is 1 MB, and packet loss rate is 0.001. In addition, it is convenient to study that the propagation delay is not considered in the simulation system.
SSi presents one of the 5 different types of traffic source in WiMAX. In order to simplify the simulation process, these five kinds of traffic sources are divided into two major categories, one is CBR traffic source, such as UGS; the other is VBR traffic source, such as rtPS, ertPS, nrtPS, BE, and the peak rate of CBR traffic source is 6.4 kbps, the mean rate of them is 6.4 kbps, accordingly, the peak rate of VBR traffic source is 6.4 kbps, and the mean rate of them is 3.2 kbps. Above all, these parameters are shown in Table 2.
![]()
Table 2. Traffic source parameters.
5.2. Simulation Results and Analysis
1) Self-Similarity of Traffics in WiMAX
Hurst parameter H is an important index to describe self-similar and long range dependence of traffics. If H of the sequences is greater than 0.5 and less than 1, the sequences have long-range dependence, otherwise, they do not. There are many methods to estimate the Hurst parameter at present; and these algorithms can estimate H values of self-similar sequences, but in the actual application, the results that they estimate is quite different. For this reason, we select Aggregated Variance method (AV), R/S method and residuals of regression (Res) to estimate the Hurst parameter of traffic in WiMAX. When the Poisson arrival rate λ equals 2, 4, 6, 8, 10 respectively, calculated H values are shown in Table 3. Accordingly, the average H that simulation obtained is 0.7854, the theoretical value H’ is 0.8, (i.e., H’ = (3 − 1.4)/2 = 0.8), then both is basically consistent, so WiMAX traffics does have the characteristics of self-similarity and long range dependence.
2) Bandwidth Utilization
To measure bandwidth utilization, arrival rate λ of VBR traffic sources is set to 5, 10, 15, 20, 25, 30, 35, 40 respectively, and arrival rate λ’ of CBR traffic sources equals 0 or 2, at the same time, in the simulation system SS-CAC algorithm and GCAC algorithm are used to perform call admission control, finally, measured bandwidth utilizations are shown in Figure 2. When the arrival rate λ of the CBR traffics is 0 and the arrival rate λ’ of the VBR traffic is less than 20 the bandwidth utilizations of two kinds of algorithm are same, after then, according to GCAC algorithm, the system is no longer accepting new calls, so that the bandwidth utilization is no longer growing, but also according to the SS-CAC algorithm the system has still remaining bandwidth, then it continues to accept the new calls and improve bandwidth utilization. The amplitude of improvement is relatively significant. When the arrival rate of the CBR traffic λ is 2, the same is true. In summary, SS-CAC algorithm has obvious advantages in bandwidth utilization. Since the CBR traffics send data at the constant bit rate in the system, as the arrival rate of CBR traffics increases, the bandwidth utilization of the same algorithm also increases.
3) Call Blocking Rate
To calculate call blocking rate in the simulation system, the arrival rate of VBR traffic and CBR traffic is set ibid, SS-CAC algorithm and GCAC algorithm is still used to make call admission control, finally, calculated call blocking rates are shown in Figure 3. As you can see from the results of the statistics, whether arrival rate λ of CBR traffics is 0 or 2, the call blocking rate of SS-CAC algorithm is significantly lower than that of GCAC algorithms. Meanwhile, Since the CBR traffic sources send data at constant bit rate, the call blocking rate will rise as arrival rate of the CBR traffic of the same algorithm increases.
6. Conclusion
As WiMAX network traffics have self-similarity and long range dependence features, we use the M/Pareto model to simulate network traffic in order to achieve higher accuracy, as well as analyse and discuss the intrinsic relationship of the M/Pareto model, the MPareto ON/OFF model and FBM traffic model in detail, also establish parameters mapping relationship of the MPareto ON/OFF model and the FBM traffic model by using M/Pareto model as a bridge. Furthermore, we derive effective bandwidth formula based on self-similarity of network traffic. As a result, a self-similar CAC algorithm is designed to improve network performance and reduce call blocking rate. Finally, Simulation results show that network bandwidth which effective bandwidth formula
![]()
Table 3. Hurst parameter values of traffics in WiMAX.
![]()
Figure 2. Bandwidth utilization increases with the arrival rate.
![]()
Figure 3. Call blocking rate increases with the arrival rate.
estimates is almost the same as actual network occupied bandwidth, and SS-CAC algorithm reduces the call blocking rate, and improves the system resource utilization and throughput. It should also be noted that the conclusions of this paper is based on assumptions that the ON period of ON/OFF model follows the same Pareto distribution. However, the actual WiMAX network traffic may not follow the same Pareto distribution. This will definitely have an influence on our conclusion and we will improve this work in the future.