Comovement of Stock Markets—An Analysis by Nonlinear Cointegration* ()


1. Introduction
In this paper we propose and develop the recursive estimation method of a nonlinear statistical model of speculative bubbles and utilize this model in establishing an idea of nonlinear cointegration. We then apply this idea to the stock market indexes of Japan and the United States, and we detect how these indexes commove in the long run although they deviate from the long-run relationship nonlinearly in the short run.
So far, whether stock markets of different countries commove together has mainly been tested by utilizing the linear cointegration relationship à la Engle and Granger (1987) [2]. We owe the main idea of cointegration to this line of research. However, what we propose in this paper is a statistical model that incorporates latent cointegration relationship not linearly but nonlinearly. The nonlinearity here stems from the consideration of booms and busts in stock price indexes (and thereby the ratio of indexes of different markets). When bubbles are born and boom for certain periods only to crash in due course, time series of these events are hardly captured by linear models.
As empirical investigation of comovement of stock markets, there have been a number of research and the results vary depending on the countries and sample periods. Asako, Zhang and Liu (2014) [3] conduct linear cointegration test among any pair of Japan, the United States and China and reach the conclusion that the linear cointegration is rejected. This is the origin of our analysis here because our daily observation suggests that the worldwide stock markets commove at any rate.
The construction of the present paper is as follows. In Section 2, we propose a time series model of the boom and bust and develop its recursive estimation method. Section 3 modifies this basic model to apply for a ratio variable, which has more restrictive feature within the model of booms and busts. In Section 4, we apply the modified model to detect the nonlinear cointegration relationship between the stock price indexes of Japan and the United States. Section 5 conclude the paper.
2. Model of Nonlinear Cointegration
In this section, we develop a model of nonlinear cointegration and explain how to estimate the relevant parameters.
2.1. The Basic Model
As an extended model to Asako and Liu (2013) [1], which in turn has its origin in Asako, Kanoh and Sano (1990) and Liu, Asako and Kanoh (2011) [4] [5], we propose a model of bubble booms and busts by, for  > 0,
> 0,
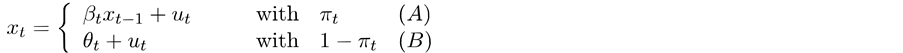 (1)
(1)
where  denotes a sequence of variables measured as the ratio of stock prices in different countries and
denotes a sequence of variables measured as the ratio of stock prices in different countries and  denotes a probability that
denotes a probability that  follows model (A) depending on
follows model (A) depending on  . A newly arisen bubble
. A newly arisen bubble  is a serially independent and normally distributed random variable with mean 0 and constant variance
is a serially independent and normally distributed random variable with mean 0 and constant variance  which is unknown to us. The coefficient
which is unknown to us. The coefficient  is a time dependent parameter whose variation is given by the following random walk process:
is a time dependent parameter whose variation is given by the following random walk process:
 (2)
(2)
Like  , the constant variance of innovations
, the constant variance of innovations  is unknown to us. Since we assume
is unknown to us. Since we assume  > 0, the probability that
> 0, the probability that  and
and  happen to bring about
happen to bring about ![]() ≤ 0 is assumed virtually nil.
≤ 0 is assumed virtually nil.
Let us consider briefly the implication of this model. Our basic model consists of two regimes or models (A) and (B). At period t, xt is expressed by a divergent time series model when a speculative bubble continues. We describe this phenomenon by the autoregressive model (A) with parameter ![]() exceeding unity. As implied by a speculative bubble, the divergent sequence will suddenly crash at a certain unknown time. We formulate this event by a systematic and probabilistic switch from model (A) to model (B). In model (B), irrespective of the position
exceeding unity. As implied by a speculative bubble, the divergent sequence will suddenly crash at a certain unknown time. We formulate this event by a systematic and probabilistic switch from model (A) to model (B). In model (B), irrespective of the position ![]() at the previous period,
at the previous period, ![]() on average returns at period t to the fundamental value θt.
on average returns at period t to the fundamental value θt.
More concretely, we assume that the probability of bubble continuation ![]() can be expressed as
can be expressed as
![]() (3)
(3)
![]() (4)
(4)
where α and γ are positive unknown parameters. This formulation implies that πt decreases as the deviation between xt and θt becomes grater in its absolute value. To put it another way, the probability of a bubble crash, 1-![]() , is an increasing function of how distant the observed bubble deviates from market fundamentals. When α = 0,
, is an increasing function of how distant the observed bubble deviates from market fundamentals. When α = 0, ![]() is independent of
is independent of ![]() and therefore the probability of crash is constant, which corresponds to the formulation given by Blanchard and Watson (1982) [6]. When α = γ = 0, the whole process is described by the autoregressive process (A) and when γ is large or
and therefore the probability of crash is constant, which corresponds to the formulation given by Blanchard and Watson (1982) [6]. When α = γ = 0, the whole process is described by the autoregressive process (A) and when γ is large or ![]() = 0, the process reduces to a simple white noise process and there is no speculative bubble. Thus, by investigating the parameter estimates, we may statistically test the properties of the process.
= 0, the process reduces to a simple white noise process and there is no speculative bubble. Thus, by investigating the parameter estimates, we may statistically test the properties of the process.
In principle, we can generalize our formulation by considering a broader class of stochastic models for ut such as ARMA process or by introducing the fundamental values into the functional form of the transition probability (3). However, we have tried to keep our model as simple as possible because this paper is only meant to be a first step in this research direction. The specification, (3), of the probability turns out to be one of the few analytically tractable formulations in the following analyses.
When the probability structure of crashes is taken into consideration, we see that the bubble cannot continue forever. As it grows, the probability of a crash approaches unity and xt will sooner or later be pulled back to the fundamental value θt. In this way, the time series of xt never diverges, but exhibits more or less stable behavior in the longer run.
Note that letting θt = 0 and assuming away the constraint xt > 0 leads us to the models of Asako, Kanoh and Sano (1990) [4], Liu, Asako and Kanoh (2011) [5] and Asako and Liu (2013) [1]. In those models, xt is not a ratio variable but is a stock price bubble measured as deviations from their fundamental values. The model of nonlinear cointegration, which is developed in Section 4, adds to this basic model the property that ratio bubbles are symmetric between upwards and downwards.
2.2. On Recursive Estimation
In Liu, Asako and Kanoh (2011) [5] and Asako and Liu (2013) [1], the entire Bayesian recursive estimation process is described for the periods from 0 to 1 and from period t-1 to period t, thus establishing by way of mathematical induction the validity of the recursive estimation method. We develop here only the recursive way of estimating parameters at period t conditioned on the available data up to period t-1. For more in detail of the entire estimation, refer to Liu, Asako and Kanoh (2011) [5] or Asako and Liu (2013) [1].
One notable difference between the present model (1)-(4) and the earlier ones is that Liu, Asako and Kanoh (2011) [5] and Asako and Liu (2013) [1] assume θt = 0. Once we allow for θt > 0, whether θt is known or unknown causes a big difference in the Bayesian recursive estimation. If it is unknown and to be estimated in the same way as the other parameters of the model, the estimation process becomes too complicated for us to manipulate the model explicitly. On the other hand, if θt is known and treated as a predetermined parameter even though we have to somehow “estimate” it eventually, this estimation can be separated from the estimation of the entire model and its recursive estimation process remains, in terms of hardness, almost at the same level as Asako and Liu (2013) [1]. In fact, we let θt be known and propose its two candidates in Section 3.
2.3. Recursive Estimation at Period t
In this section, we describe a Bayesian recursive technic to estimate the parameters of our model. Before proceeding to this task, we put ![]() the set of data observations up to period t, and by
the set of data observations up to period t, and by ![]() , we denote the set of ordered integer indices where each is (s = 1; 2; : : : ; t) is either 1, 2, or 3.
, we denote the set of ordered integer indices where each is (s = 1; 2; : : : ; t) is either 1, 2, or 3.
With these new notations, we write down the joint density for ![]() ,
, ![]() conditional on
conditional on ![]() :
:
![]() (5)
(5)
where ![]() and
and ![]() are certain deterministic functions of
are certain deterministic functions of ![]() that are to be determined in the sequel so as to satisfy the recursive pattern, whereas P(.) and N(.) denote density functions;
that are to be determined in the sequel so as to satisfy the recursive pattern, whereas P(.) and N(.) denote density functions; ![]() is the joint prior density function for constant
is the joint prior density function for constant ![]() and
and ![]() 1 over time conditioned on Xt and
1 over time conditioned on Xt and ![]() is the density function of the normal distribution with mean
is the density function of the normal distribution with mean ![]() and variance
and variance ![]() . Their detailed functional forms as well as the definition of the other factors on the right-hand-side of (4) are given immediately below. Note that the summation is over the entire combination of indices which amount to 3t-1 terms at stage t. Then, in view of (2), the joint prior density function for
. Their detailed functional forms as well as the definition of the other factors on the right-hand-side of (4) are given immediately below. Note that the summation is over the entire combination of indices which amount to 3t-1 terms at stage t. Then, in view of (2), the joint prior density function for ![]() ,
, ![]() , and
, and ![]() conditioned on
conditioned on ![]() is
is
![]() (6)
(6)
Now our main task is to calculate the updated posterior density (6) by utilizing the Bayes’ theorem:
![]() (7)
(7)
Introducing a new parameter
![]() (8)
(8)
for the sake of later convenience in notation, from (1) and the normality of ut, we have
![]() (9)
(9)
Therefore, in view of (7), the multiplication of (6) and (9) yields the updated formula of (6) for period t if and only if we have, to begin with
![]() (10)
(10)
where the first and second terms within the large brackets represent, respectively, the probability density function of exponentially and mutually independently distributed ![]() and
and ![]() 2. The integer function
2. The integer function ![]()
![]()
is introduced to simplify the mathematical expression.
Moreover, for the unspecified coefficient functions, we must have
![]() (11)
(11)
and
![]() (12)
(12)
Also for means and variances of the normal distributions, it must be
![]() (13)
(13)
and
![]() (14)
(14)
Finally, it must be recalled, that by making use of the relationship that applies for conditional density functions
![]() (15)
(15)
and knowing that ![]() are mutually independent in (6), we immediately obtain
are mutually independent in (6), we immediately obtain
![]() (16)
(16)
which appears in the denominators of (7) and (11). This establishes all requirement that enable Bayesian recursive estimation to update consistently.
2.3.1. Parameter Estimates
The estimates of ![]() at period t are the conditional expectations on
at period t are the conditional expectations on ![]() . Thus, referring to period t by suffix t, we have
. Thus, referring to period t by suffix t, we have
![]() (17)
(17)
![]() (18)
(18)
and
![]() (19)
(19)
We also obtain the probability estimate of bubble continuation from period t-1 to t as
![]() (20)
(20)
or we can directly obtain the conditional expectation as
![]() (21)
(21)
Finally, the estimate of the variance of ![]() is given by
is given by
![]() (22)
(22)
2.3.2. Maximum Likelihood Estimates of Variances
In carrying out the recursive procedure explained above, two variance parameters are to be specified. These are the dispersions of the random terms in (1) and (2), i.e., ![]() and
and ![]() . The likelihood function for these parameters can be obtained in the following way.
. The likelihood function for these parameters can be obtained in the following way.
Let us put ![]() for simplicity. The likelihood function for
for simplicity. The likelihood function for ![]() with T periods of data is defined as
with T periods of data is defined as
![]()
On the other hand, since
![]() (24)
(24)
and
![]() (25)
(25)
we have, like (16)
![]() (26)
(26)
Therefore, the log likelihood function of ![]() can be expressed by
can be expressed by
![]() (27)
(27)
and the resulting set of variances ![]() which maximize (27) are the desired estimates.
which maximize (27) are the desired estimates.
2.3.3. Condensation of Recursive Estimation
So far is the complete and mathematically rigorous description of the Bayesian recursive estimation and we can estimate parameters for any length of sample periods. However, the number of terms we need to compute in equations from (11) to (14) and others increases at a rate of 3t to exceed a standard capacity of computer as the number of time series data increases. For this reason and to reduce the computational burden, we introduce the so-called condensation procedure first proposed by Harrison and Stevens (1981) [7] and applied for the estimation of the basic model by Liu, Asako and Kanoh (2011) [5] and Asako and Liu (2013) [1]. By condensation, we update the parameters of the next period’s prior distribution by utilizing the first and second moments of the approximated marginal posterior distribution. This enables the computational burden to remain at a constant level over time.
What we have to do in practice is to approximate the posterior density (5) at period t or the left hand side of (7) by a joint density of the following form
![]() (28)
(28)
where we utilize the fact that ![]() ,
, ![]() , and
, and ![]() are mutually independent. Then the first and second moments of the marginal densities for each parameter are equated. That is, (5) at period t is approximated by
are mutually independent. Then the first and second moments of the marginal densities for each parameter are equated. That is, (5) at period t is approximated by
![]() (29)
(29)
so that the joint prior density at period t + 1 can be written as
![]() (30)
(30)
where ![]() and
and ![]() are equated, respectively, to the reciprocal of the mean estimates (17) and (19)
are equated, respectively, to the reciprocal of the mean estimates (17) and (19)
![]() (31)
(31)
![]() (32)
(32)
whereas ![]() and
and ![]() are estimates given by (18) and (22). This procedure can be repeated at each stage.
are estimates given by (18) and (22). This procedure can be repeated at each stage.
2.4. Nonliner Cointegration
The basic bubble model (1)-(4) formulates the feature that a ratio variable returns to its fundamental value in the long run as the probability that a bubble crashes reaches 100% insofar as the divergent bubble continues. In other words, although short-run bubbles generate explosive discrepancies between ![]() and θt, divergent booms would bust eventually and in this sense there is a stable relationship in the long run. This phenomenon is what we call the nonlinear cointegration.
and θt, divergent booms would bust eventually and in this sense there is a stable relationship in the long run. This phenomenon is what we call the nonlinear cointegration.
Unlike the definition of linear cointegration, the definition of nonlinear relationship is model-specific. There may be other models of nonlinear cointegration and our nonlinear cointegration should more restrictively be named speculative bubble nonlinear cointegration or boom and bust nonlinear cointegration.
Such being the case, there is no established method to test the nonlinear cointegration relationship. Instead, we are obliged to accept the existence of the nonlinear relationship only passively. We especially put emphasis on the bubble process in (2) and thereby we detect whether ![]() and how often switches occur between two models or how high is the probability of bubble continuation
and how often switches occur between two models or how high is the probability of bubble continuation ![]() .
.
In the empirical analysis in Section 4, we compute the pseudo-t statistics:
![]() (33)
(33)
in order to sense the “significance“ regarding the validity of βt > 1. Since the present estimation technic is Baye- sian in the sense that we utilize prior information besides the information extracted from the data, statistics like (33) may not obey Student’s t-distribution. Nonetheless, we would presume that t = 1.65, which is one sided 5% significant for a standard t test, is a critical level to rely on.
In detecting the validity of the nonlinear cointegration, we may as well examine into the probability of bubble continuation ![]() . We check in Section 4 the probability of bubble crash, 1-
. We check in Section 4 the probability of bubble crash, 1-![]() , and see its movement over time.
, and see its movement over time.
3. Nonlinear Cointegration: Modification of the Basic Model
The basic model we developed in Section 2 is applicable to any series of xt. In this section, we modify the basic model to deal with a ratio variable xt > 0.A ratio variable may exhibit both upwards and downwards bubble processes with θt > 0, which necessitates certain nontrivial revision in recursive estimation.
3.1. Modification of the Basic Model
We alter the basic model into a double regime switching model. One regime switching is that the basic model is of the boom-and-bust type. The other regime switching is that a ratio variable has both upwards (or positive) and downwards (or negative) bubble processes. On the other hand, we maintain (2) or the transition equation of ![]() as it is.
as it is.
Then, we can naturally regard it a bubble by βt > 1 once ![]() keeps increasing over time. But even when
keeps increasing over time. But even when ![]() keeps decreasing by a downwards bubble, estimates may end up with βt < 1 for certain periods of time. In such a case, we may misunderstand what is really happening because βt < 1 is usually a case for a stationary autoregressive process. This is quite embarrassing and we may as well be advised to treat the upwards and downwards bubbles asymmetrically. For this aim, we take the reciprocal of the original ratio when the ratio itself is smaller than θt as in (3), thus resulting in a drastic regime switch for negative downwards bubbles.
keeps decreasing by a downwards bubble, estimates may end up with βt < 1 for certain periods of time. In such a case, we may misunderstand what is really happening because βt < 1 is usually a case for a stationary autoregressive process. This is quite embarrassing and we may as well be advised to treat the upwards and downwards bubbles asymmetrically. For this aim, we take the reciprocal of the original ratio when the ratio itself is smaller than θt as in (3), thus resulting in a drastic regime switch for negative downwards bubbles.
Let ![]() represent an original ratio variable of two stock prices, and let us redefine xt by
represent an original ratio variable of two stock prices, and let us redefine xt by
![]() (34)
(34)
With this new xt,, we assume that every aspect of the basic model (1)-(4) is valid, i.e.,
![]() (35)
(35)
except that
![]() (36)
(36)
replaces (8).
Note that integrating artificially two regimes most likely causes heteroscedasticity in innovation term ut in (1) or (35). In fact, we will introduce proportional variance of ut to ![]() squared in our empirical analysis in Section 4:
squared in our empirical analysis in Section 4:
![]() (37)
(37)
Lastly, we need to revise the probability of bubble continuation. That is, in (3), we have
![]() (38)
(38)
or
![]() (39)
(39)
that replaces (4). In (38) or (39), the greater deviation is ![]() for the positive upwards bubble and
for the positive upwards bubble and ![]() = 1/yt − 1/θt for the negative downwards bubble.
= 1/yt − 1/θt for the negative downwards bubble.
3.2. Known θt
As we have already noted, the fundamental stock prices ratio θt is assumed known and given to us exogenously at period t. There may be several candidates for θt. Here we propose two alternative ones3.
3.2.1. Past Average
The first candidate is the simple arithmetic average of all the past data:
![]() (40)
(40)
Although we put equal weight on each data, the informational role of the current data decreases over time as (40) by definition is rewritten as θt = {(t-1) θt-1+yt}/t, which in turn is rewritten as
![]() (41)
(41)
Equation (41) implies that θt follows a random-walk type sticky movement except that the drift term is not stochastic but is given deterministically. As t increases, the contribution of the second term on the right hand side of (41) decreases over time.
3.2.2. Fixed Period Moving Average
The second candidate approximates the fundamental value by the fixed period (say 12 months) moving average up to the current one. Thus in place of (40) we have
![]() (42)
(42)
And thereby in place of (41), we have
![]() (43)
(43)
for t > 12. As for the first 12 months, we use the simple average (40).
3.3. Estimation Procedure at Period t
At period t, we compute θt once we get a new data yt and we determine which regime we are in, i.e., whether a positive bubble (yt ≥ θt) or a negative bubble (yt < θt). If we are rigorously interested in whether the stock price ratio is in positive upwards phase or in negative downwards phase, we may watch where we have been in the past. For example, we would recognize regime shifts only if the opposite new regime continues at least a few consecutive periods. This will exclude a fake regime shift that occurs unsystematically. The idea of this rule of thumb stems from the Bry-Boschan method in the judgment of the business cycle phase.
Once θt and thereby the data xt of (34) is obtained, we are ready to utilize the recursive estimation technic developed in Section 2. We estimate the basic model as applied to the stock market prices of Japan and the United States.
4. Stock Prices of Japan and the United States
Asako, Zhang and Liu (2014) attempted to apply the nonlinear cointegration to the stock markets of Japan, the United States and China. They first checked whether there is a linear cointegration relationship between these countries and concluded negatively for any pair of countries. Then they estimated the basic model of (1)-(4) and of three ways of the known fundamental stock prices ratio including (40) and (42). Among these, in what follow, we develop the most representative case of the nonlinear cointegration; namely the one between the stock price indexes of Japan and the United State.
4.1. Preparatory Steps
The monthly time series data we have chosen are the Nikkei225 index (hereinafter Nikkei225) for Japan and the Dow-Jones Industrial Average Stock Price Index (hereinafter DJ) for the United States. Figure 1 plots these stock prices and their ratio (DJ/Nikkei225) from January 1970 to December 2012.
4.1.1. Derivation of Known θt
Figure 2 exhibits the fundamental stock prices ratio given by (40) and (42). Not surprisingly, (i) the past average ![]() shows a random-walk type sluggish swing whereas (ii) the fixed period moving average
shows a random-walk type sluggish swing whereas (ii) the fixed period moving average ![]() traces short lived ups and downs around the historical actual path of the ratio yt.
traces short lived ups and downs around the historical actual path of the ratio yt.
4.1.2. Artificial Dependent Variable
Next, we construct from the time series yt that of the artificial variable xt by (34). Referring to the realized yt and two fundamental stock prices ratio θt, the time series of xt consists of negative bubble (yt < θt) up to the mid 1990s and thereby, by definition, xt equals the reciprocal of yt. On the contrary, during the latter half of the sample period, xt consists of positive bubble (yt > θt) and xt is yt itself. In the case of ![]() , however, yt > θt and yt < θt interchange with small intervals, as does xt.
, however, yt > θt and yt < θt interchange with small intervals, as does xt.
4.1.3. Maximum Likelihood Estimates of Variances
We need to obtain the maximum likelihood estimates for the variances of ![]() in (1) and
in (1) and ![]() in (2). We also have to set initial values in beginning the recursive estimation. The effect of the initial conditions turns out to be minimal as we tried several combinations to result in little difference in the main feature of estimation except for several initial periods. The final choice was
in (2). We also have to set initial values in beginning the recursive estimation. The effect of the initial conditions turns out to be minimal as we tried several combinations to result in little difference in the main feature of estimation except for several initial periods. The final choice was ![]() = 1,
= 1, ![]() , and
, and ![]() =
= ![]() = 0.01 and denoting by
= 0.01 and denoting by ![]() the pair of standard deviations, the maximum likelihood estimates were (0.0536, 0.0000) for
the pair of standard deviations, the maximum likelihood estimates were (0.0536, 0.0000) for ![]() and (0.0456, 0.0000) for
and (0.0456, 0.0000) for ![]() . The resultant log likelihoods were 377.9 and 600.7, respectively.
. The resultant log likelihoods were 377.9 and 600.7, respectively.
Judging on the log likelihood, between the two fundamental stock prices ratio, ![]() fits the data better than
fits the data better than ![]() does. Knowing this consequence, we yet report those alternative fundamental values as these yield really comparable estimation results as we explain in the sequel4.
does. Knowing this consequence, we yet report those alternative fundamental values as these yield really comparable estimation results as we explain in the sequel4.
![]()
Figure 1. Stock Price Indexes: Japan and the US. Note) The Nikkei225 for Japan and DJ for the United States.
4.2. Necessary Condition for the Bubble
With the above preparation, Figure 3 exhibits the estimate of the key parameter βt. The percentage of samples that satisfies the necessary requirement for bubbles βt > 1 amounts to 82.9% for ![]() and 100% for
and 100% for ![]() among the entire 43 years’ sample periods (516 months from 1970; 1 to 2012;12). Namely with both
among the entire 43 years’ sample periods (516 months from 1970; 1 to 2012;12). Namely with both ![]() and
and ![]() , samples with βt > 1 exceed more than 80%. These observations may as well support the view that the model (1)-(4) with reasonable modification fits the data and the stock markets of Japan and the United States are cointegrated nonlinearly in the long run. But how reliable is this result?
, samples with βt > 1 exceed more than 80%. These observations may as well support the view that the model (1)-(4) with reasonable modification fits the data and the stock markets of Japan and the United States are cointegrated nonlinearly in the long run. But how reliable is this result?
To answer to this question, we checked the pseudo t t-statistic (33) and found, as summarized in Table 1, that βt > 1 is one sided 5% “pseudo-significant” is nil for ![]() and 93.0% for
and 93.0% for ![]() (similarly the nonstationarity condition βt < 1 is not significant). These suggest that the standard deviation of βt is relatively large, and the reliability of the estimates is limited. Note, on the contrary, that βt > 1 is 93.3% pseudo-significant for
(similarly the nonstationarity condition βt < 1 is not significant). These suggest that the standard deviation of βt is relatively large, and the reliability of the estimates is limited. Note, on the contrary, that βt > 1 is 93.3% pseudo-significant for ![]() .
.
A clue to this is that the maximum likelihood variance estimate ![]() is extremely small and is virtually the corner solution at zero. In this case, the key parameter βt is theoretically regarded constant in (2). But, like the parameters
is extremely small and is virtually the corner solution at zero. In this case, the key parameter βt is theoretically regarded constant in (2). But, like the parameters ![]() and
and ![]() , the estimate of βt does not have to stay unchanged over time. Even if the variance of
, the estimate of βt does not have to stay unchanged over time. Even if the variance of ![]() is 0 in (2), we have
is 0 in (2), we have
βt = βt-1 + constant,
and βt can be different from βt-1. Moreover, even if the constant term is 0 and βt = βt-1, in theory, because βt is estimated as the expected value of the posterior distribution à la Bayesian, it can differ from βt-1 once the data increases information in the posterior distribution in (18).
4.3. Probability of Bubble Crash
In Figure 4, we plot the probability of bubble crash, 1-πt. As πt, the conditional expectation (21), rather than the point estimate (20), is chosen5. With ![]() the crash probability remains small except for the early 1970’s, which seems to be a transitional feature incorporating specific initial conditions, whereas with
the crash probability remains small except for the early 1970’s, which seems to be a transitional feature incorporating specific initial conditions, whereas with ![]() the probability repeatedly rises and falls depending on the state of bubbles.
the probability repeatedly rises and falls depending on the state of bubbles.
4.4. Other Cases
Asako, Zhang and Liu (2014) [3] estimate several other cases including exchange rate adjusted stock prices, the
![]()
Table 1. Number of months of the estimated βt.
case of Var (![]() ) =
) = ![]()
![]() instead of (37), stock prices ratio of Japan and China, and that of China and the United States. The estimation results vary case by case but reaches the conclusion that the basic model (1)-(4) and its modification with βt > 1 fits the data reasonably well, thus establishing the latent nonlinear boom and bust relationship between relevant stock prices.
instead of (37), stock prices ratio of Japan and China, and that of China and the United States. The estimation results vary case by case but reaches the conclusion that the basic model (1)-(4) and its modification with βt > 1 fits the data reasonably well, thus establishing the latent nonlinear boom and bust relationship between relevant stock prices.
5. Concluding Remarks
In this paper we proposed and developed the recursive estimation method of the nonlinear cointegration. The purpose of this attempt has been to show the usefulness of introducing the idea of nonlinear cointegration. By applying this idea to the stock market indexes of Japan and the United States, we have seen that these indexes commove in the long run although they deviate from this relationship in the short run.
NOTES
![]()
*We thank JSPS for Grants-in-Aid for Scientific Research B (24285062). Remaining errors are the whole responsibility of the authors.
![]()
1Even if we instead allow for time dependent α and γ, the computational burden remains the same as α and γ are at any rate estimated differently over time.
![]()
2We assume that α and γ are exponentially distributed in accordance with the exponential probability of the bubble continuation (3).
![]()
3We may find some variables Zt that are to be reflected in the fundamentals θt. Then the fitted value of an OLS regression equation of xt on Zt appears to be another candidate. However, the estimate of θt thus constructed is neither consistent nor efficient, if not unbiased.
4This ordering is not robust. When we assume away the heteroscedastic variance (37), log likelihood becomes larger with ![]() than the one with
than the one with ![]() .
.
![]()
5Two estimates are very close and are the same to three or four decimal places.