Design of the Quantization Matrix in the Distributed Compressed Sensing Video Coding* ()

1. Introduction
With the increasingly complex and changeable monitoring environment, the simple data obtained by the traditional wireless sensor networks does not meet the complete need of the people for monitoring the environment. For achieving the accurate monitoring of the environmental information, it is an active demand that we introduce the media of the image, audio and video with abundant information into the environment monitoring activities based on the sensor networks. in this context, the wireless multimedia sensor networks emerge as the times require [1]. In the wireless multimedia sensor networks, the technology of the traditional video coding does not meet the low complexity requirement of the wireless multimedia sensor networks for the nodes. The traditional video coding plan using the technology of “Joint Coding, Joint Decoding” [2]. This technology have a very high compression efficiency, but it is very sensitive to the channel error. The error propagation happens easily under the situation for the high rate of channel error. It leads to an unsatisfactory result of the effect of reconstruction the images [3]. For resolving this issue, the researcher considered a method composed of data collection and compression totally different from the traditional collection method base on Nyquist Rate, which is the compressed sensing.
The theory of the compressed sensing is a new theory of the new signal processing presented by Z. X. Tao, Donoho, et al. in the year of 2006 [4]. It broke the bottleneck of the Nyquist Theorem. It combines the collection and the compression and uses the optimization algorithm reconstruction at the collecting terminal. It is featured on the advantage of simple coding and strong capacity of anti-errors. It does meet the requirement of the wireless multimedia sensor networks. In the recent years, in the wireless multimedia networks, the theory of the compressed sensing has been applied to the distributed video coding. For example, the WINES Laboratory leaded by Professor T. Melodia of New York Buffalo devotes themselves to the research of the video coding transmission plan based on the compressed sensing under the wireless multimedia sensor networks [5], and they have already gained a lot of achievements.
2. Relative Basic Theory
2.1. Compressed Sensing
The Compressed Sensing theory broke the bottle neck of the Nyquist Sampling Theorem. It combines the processing of the sampling and compression, and uses the non-adaptive linear projection for maintaining the original structure of the image signal, and can rebuild effectively the image signals by the optimization algorithm at the receiving terminal. In the compressed sensing theory, the image is represented as the vector 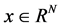 and the length of the vector is represented as N. The reversible transformation matrix
and the length of the vector is represented as N. The reversible transformation matrix 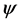 of N*N exists hypothetically. It meets
of N*N exists hypothetically. It meets
 (1)
(1)
In this equation,  is the K-sparse vector, that is
is the K-sparse vector, that is 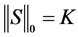 and K < N.
and K < N.  represents that is the norm of p. It means that transform the image by a certain transformation into certain field could be sparse, for example, wavelet transform. Then, M measuring values are taken out from N values of x. It is required that M < N. This step is achieved by the measuring matrix
represents that is the norm of p. It means that transform the image by a certain transformation into certain field could be sparse, for example, wavelet transform. Then, M measuring values are taken out from N values of x. It is required that M < N. This step is achieved by the measuring matrix 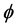 as follows.
as follows.
 (2)
(2)
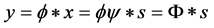 (3)
(3)
After receiving y at the receiving terminal, the x needs to be recovered. As M < N, the system is underdetermined, that means it is countless solutions. If a solution 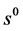 meets the Equation (3), the vector
meets the Equation (3), the vector  (the n represents the empty matrix of the same size as
(the n represents the empty matrix of the same size as ), it also meets the Equation (3). By the proof of the theory, if the measuring matrix
), it also meets the Equation (3). By the proof of the theory, if the measuring matrix 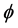 and the transformation matrix
and the transformation matrix 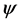 are uncorrelated, and the sparsity K is smaller than the specified threshold, we can get the s which meet the requirements by the most sparse solution of the Equation (3). The most sparse solution corresponds to the y of the receiving terminal. It is a NP-hard problem [6]. There is always the sparsest solution for the matrix
are uncorrelated, and the sparsity K is smaller than the specified threshold, we can get the s which meet the requirements by the most sparse solution of the Equation (3). The most sparse solution corresponds to the y of the receiving terminal. It is a NP-hard problem [6]. There is always the sparsest solution for the matrix 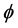 and this solution is sole. It equals to the following equation:
and this solution is sole. It equals to the following equation:
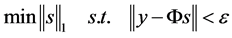 (4)
(4)
In this equation, 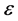 is the smallest threshold. Thus, the problem is transformed to an optimal solution problem. By the transformation matrix
is the smallest threshold. Thus, the problem is transformed to an optimal solution problem. By the transformation matrix![]() , and both of the measuring matrix
, and both of the measuring matrix ![]() and the received y can be proceeded the reconstruction of x [7].
and the received y can be proceeded the reconstruction of x [7].
2.2. DVC: Distributed Video Coding
In the Distributed Video Coding based on the theory of information coding presented by Slepian, Wolf, Wyner and Ziv in the seventies of last century [8], we run independently the coding work at the coding end and run the joint decoding work at the decoding end according to the relativity of the time domain and the space domain of the video sequences and transform the complexity from the coding end to the decoding end. The characteristics of the Distributed Video Coding adapt well the requirements of the Wireless Multimedia Sensor Networks. The Distributed Video Coding has become the hottest research in the recent years. With the presentation of the Compressed Sensing Theory, D. Baron et al. introduced the compressed sensing theory into the distributed video coding and presented a completely new theory of signal processing, that is the Distributed Compressive Video Sensing [9]. The research of this article is based on the frame of the distributed compressive sensing as Figure 1.
The research of the distributed compressive sensing is divided into the research of the sparse representation algorithm of the coding end, the research of the reconstruction algorithm of the decoding end and the research of the transmission strategy in the transmission process. We don’t consider the influence of the sparse representation algorithm and the reconstruction algorithm in this article. We study the influence of the quantization method in this article and design and achieve the new quantization matrix adapting to the distributed compressive sensing video coding.
3. Gaussian Quantization Matrix
3.1. Distribution of the Measuring Coefficient of the Compressed Sensing
The design of the quantizer is vital in the transmission system. A good quantizer can improve effectively the reconstruction quality at the coding end. We will present a new Gaussian quantization matrix base on the compressed sensing distributed video coding in this section.
In the previous studies, different standard of video coding corresponds the different design of the quantization matrix. For example, in the first image of the announcer video sequences, under the MEPG standard, the distribution of the coefficient after discrete cosine transform can be seen as Figure 2(a). The distribution of the coefficient of the image concentrate mainly in the low frequency region in Figure 2(a), so the design of the quantization matrix follows also the standard of small quantization step in the low frequency region and big quantization step in the high frequency region, that is the dense quantization in the low frequency region and the sparse quantization in the high frequency region [10]. This is also conforming to the theoretical basis of vision of
![]()
![]()
Figure 1. DCVS Frame of the sending end and receiving end.
![]()
![]() (a) (b)
(a) (b)
Figure 2. Histogram of the distribution of the parameters. (a) DCT parameters; (b) CS measuring parameters.
human eyes as the vision of human eyes isn’t sensitive to the errors of the high frequency part while is sensitive to the low frequency part.
The idea of the compressed sensing is that the sparse matrix in a certain projection domain is transformed to another one projection domain and the sparsity of the matrix is increased, therefore it plays the role of signal compression. The distribution of the image coefficients after measuring by the compressed sensing can be known from Figure 2(b). Comparing with the distribution Figure of the coefficients after the DCT (discrete cosine transform), the parameters are also concentrated around the 0 and the large value data of both sides are very few. As we can see in Figure 2(b), the distribution of the parameters after the compressed sensing is the Gaussian distribution (normal distribution).
The distribution of the measuring coefficients of the compressed sensing refers to the histogram 2b.The distribution of the image coefficients after compressed sensing is the Gaussian distribution. Meanwhile, as the characteristic that the vision of human eyes isn’t sensitive to the high frequency error but sensitive to the low frequency error, if the design of the quantization matrix also follows the Gaussian distribution, the distribution of the coefficients of the quantization matrix is also the Gaussian distribution. The better quantization effect will be achieved by this kind of quantization matrix. We call it as the Gaussian Matrix in this article.
3.2. Design of Gaussian Quantization Matrix
The Gaussian Quantization Matrix obtained by the characteristic of the distribution of the coefficients after the measuring of the image. The distribution of the coefficients of the quantization matrix depends on the distribution ratio of the coefficients after measuring. The coefficients of the first image of the announcer video sequences after measuring is presented through the histogram in Figure 2(b). Before measuring the image coefficients, we proceed the operation of reducing the mean from all of the coefficients in order to increase the sparsity. The distribution of the coefficients of Figure 2(b) is visualized and the parameters are showed quantitatively in Table 1.
The Gaussian Quantization Matrix designed in this article, the distribution of the quantitative coefficients also follows the specific gravity distribution of the image coefficients. As we can observe from the data in Table 1, the part nearby the 0 is in the dense quantization and the part far away from 0 is in the sparse quantization. We define this distribution function similar to the Gaussians as
![]() (5)
(5)
We can find after analyzing carefully Table 1, at the both ends far away from 0, the rate of the coefficients numbers in the total coefficients is very small and it is almost 0. If the dense quantitative parameters are nearly the 0, but there isn’t any quantitative coefficient at the region far away from the 0. The effect of such kind of quantization matrix isn’t good. In fact, after processing by compressed sensing, the coefficients of the image will concentrate to the part of small value. However, a lot of image information is also saved in the big value data. So we can’t run a too crude quantization for the big value data. The solution is to run a certain degree of uplift for the Gaussian distribution function. Uplift the Gaussian distribution according to the Equation (6).
![]() (6)
(6)
We add the average value of the coefficients of the previous image to the standard Gaussian distribution and change effectively the distribution of the quantization coefficients by this way. The quantization matrix can be obtained by programming after understanding the distribution of the quantization coefficients. The histogram of the distribution of the quantization matrix is presented in Figure 3 through the quantization matrix obtained in the distribution of the image coefficients. The matching effect of the distribution of the quantization coefficients and the measuring coefficients in the histogram is very good. The effect of the quantization matrix can be verified by the subsequent experimental simulations.
4. Comparison of the Effects
We analyze the experimental simulation of the Akiyo video sequences in this article. From the comparisons of the reconstruction effect of 3 kinds of quantitative methods in Figure 4 & Figure 5, we can know that the reconstruction effect is the best when we don’t make any quantization for the video sequences. Apparently, the quantitative error won’t be introduced if we don’t make any quantization, and the high accuracy of the data can be ensured, therefore, the high quality of the reconstruction can be assured. However, the quantity of the image data will not be compressed if we don’t make any quantization, and the high accuracy of the data will become the encumbrance of the transmission and the reconstruction processing, so the time consumption of the method of non-quantization is the longest.
![]()
Table 1. Distribution of the coefficients after measuring the compressed sensing of the image.
![]()
Figure 3. Histogram of the distribution of the coefficients of the Gaussian quantization matrix.
![]()
Figure 4. Comparison of uniform and Gaussian quantization.
![]()
Figure 5. Comparison of Gaussian non Gaussian quantization.
Due to the same quantization series, the sizes of the Gaussian Quantization Matrix and the Uniform Quantization Matrix are same too, so the time consumptions are also almost the same. However, as we can see from the comparison of the reconstruction effect of the simulation results, the quantization effect of the Gaussian Quantization Matrix is better than that of the Uniform Quantization Matrix. The reconstruction effect of the Uniform Quantization of some individual frames is better, but in general, the advantage of the Gaussian Quantization is more apparent. Moreover, we compared the H.264 Standard Quantization Algorithm with the Lloyd Quantization Algorithm and the Gaussian Quantization, and the results are as shown in Figure 6. As we can see from the figure, the effect of the H.264 Standard Quantization Algorithm is worse than that of the Lloyd Algorithm and the Gaussian Quantization, and the effect of the Gaussian Quantization and the Lloyd Quantization is the same, that is to say that the Lloyd Quantization is better at some points and the Gaussian Quantization is better at some other points. The quantization effect of the Lloyd Quantization Algorithm is close to that of the Gaussian Quantization, however, for the Lloyd Quantization Algorithm, we take a sample and a uniform quantization matrix as the training sample and the Lloyd Quantization Matrix is achieved after much iteration, therefore, the achievement of the Lloyd Quantization Matrix is a process with a big time-consumption. For the Gaussian Quantization Matrix, the Gaussian Matrix can be achieved only by the simulation software and then the sparse distribution of the Gaussian Matrix can be adjusted as required by the equation operation. The time consumption of the 3 kinds of quantization methods are as shown in Table 2.
![]()
Figure 6. H.264 comparison of the effects of the standard quantization, Lloyd quantization and the Gaussian quantization.
![]()
Table 2. Table of time consumption of the generations of the Gaussian quantization matrix and the Lloyd quantization matrix.
As we can see from Table 2, the time consumption of the generation of Gaussian Quantization Matrix is 0.1851 s, and the time consumption of the generation of the Lloyd Quantization Matrix is 1.8034 s and it is almost 10 times of that of Gaussian Quantization Matrix. Under the situation of the approximative effects, the time consumption of the generation of the Gaussian Quantization Matrix is only one tenth of that of the Lloyd Quantization Matrix.
5. Conclusion
In this article, we analyze the characteristics that the distribution of the image coefficients is as the Gaussian Distribution and the distribution of the quantization matrix coefficients of the Gaussian Quantization Matrix is also the Gaussian Distribution under the distributed compressive sensing video coding, and then make the comparison with the Uniform Quantization, and finally, we got the conclusion that the effect of the new quantization matrix is better. The effect of the Gaussian Quantization is not as good as that of the non-quantization method, however, from the point of the efficiency, the time consumption of the Gaussian Quantization Matrix is much smaller than that of the non-quantization method. The time consumptions of the Gaussian Quantization and the Uniform Quantization are the same as the quantization parameters and the quantization matrix of these 2 kinds of quantization matrix are the same. By such comparison, we can achieve the conclusion that both of the effect and the efficiency of the Gaussian Quantization Matrix are better.
NOTES
![]()
*This work is financially supported by NSFC Projects No. 61471162, NSF of Jiangsu Province (BK20141389), and Innovation Project of Nanjing Institute of Technology (ZKJ201305, QKJA201304)