Received 15 March 2016; accepted 17 May 2016; published 20 May 2016

1. Introduction
Bayesian networks emerged about three decades ago as alternatives to conventional systems-oriented decision- making and forecasting under uncertainty in probabilistic terms [1] . A Bayesian network is a statistical tool that represents a set of associated uncertainties given conditional independence relationships established between them [2] [3] .
The rule Bayes is a rigorous method for interpreting evidence in the context of previous experience or knowledge. The Bayes rule has recently emerged as a powerful tool with a wide range to applications which include: genetics, image processing, ecology, physics and engineering. The essential characteristics of Bayesian methods are their explicit use of probability for quantifying uncertainty in inferences base on statistical data analysis. A Bayesian probability interval for an unknown quantity of interest can be directly regarded as having a high probability of containing the unknown quantity, in contrast to a frequentist confidence interval which may strictly be interpreted only in relation to a sequence of similar inferences that might be made in repeated practice.
Using Bayesian networks as a tool for data analysis is not widespread in the context of Psychology. However, the benefits of using this tool in all areas of psychology are identified in several ways: on the economic front with Bayesian networks could develop systems to make judgments appropriate chance to improve diagnosis and psychological treatment. On the scientific level, Bayesian networks cannot be overlooked if psychology strives to clarify the mechanisms by which people evaluate, decide and make inferences; as they may serve as analytical and theoretical reference in the development of models of reasoning, learning and perception of uncertainty [3] .
In psychology, the area’s most prolific work in the use of Bayesian networks has been the causal learning [4] - [7] , where they test the hypothesis that people represent causal knowledge similarly to as it does a Bayesian network. Other theoretical developments have made possible to extend the use of Bayesian network outside the domain of causal knowledge, for instance, on inductive generalization of concepts and learning words [8] . Another facet of Bayesian networks which have proved useful tools is in market research [9] . Others found that a Bayesian network classifies customers of a company relative to the perspective of long-term purchases [10] . On the other hand, it analyzed the nature of human emotions and the negative behavior resulting from overcrowding during mass events. Utilizing the Bayesian network, his model shows the dependence structure between different emotions and negative behaviors of pilgrims in the crowd [11] .
Finally, by its shaping power, the Bayesian networks could be used to generate more and better models of how organizations, groups or social aggregate which is the subject of study for psychology. Thus the aim of this study was to determine the underlying causal structure of the elements of happiness from a set of empirically obtained data. It is considered a Bayesian statistical parameter, which is inferred as an uncertain event, in this study the knowledge about happiness is not accurate and is subject to uncertainty, therefore happiness can be described by a probability distribution. Whereby the Metropolis algorithm used is a specific type of process Monte Carlo, which generates a random way so that every step along the way is completely independent of the previous steps of the current position and generates Markov chains. Process in each step has not memory of the previous states. This is known as Markov Chain Monte Carlo (MCMC)
Happiness has been defined as an entity that can be described by a specific set of measures [12] , [13] , a mental state that people can gain control over in a cognitive way to perceive and conceive both themselves and their world as an experience of joy, satisfaction or positive welfare [14] . Unfortunately, terms like happiness have been used frequently in daily discourse and may now have vague and somewhat different meanings.
The difficulty of defining happiness has led pioneer psychologists in the study of happiness propose the term subjective well-being (SWB). SWB refers to people's evaluations of their own lives and encompasses both cognitive judgments of satisfaction and affective appraisals of moods and emotions. This conceptualization emphasizes the subjective nature of happiness and holds individual human beings to be the best judges of their own happiness [15] - [17] .
There is empirical evidence indicating that well-being is a much broader construct than stability of emotions and subjective judgment about life satisfaction; e.g. situational models consider that the sum of happy moments in life results in the satisfaction of people [18] , that is, a person exposed to a greater amount of happy events will be more satisfied with his or her life. People briefly react to good and bad events, but in a short time they return to neutrality. Thus, happiness and unhappiness are merely short-lived reactions to changes in people [19] and it depends strongly on intentional activity [20] , [21] . But also it has been identified the temperament is suggested to influence happiness [22] , [23] and other personality traits such as optimism and self-esteem [24] - [26] , the self-determination [27] .
Scholars have noticed that happiness is not a single thing, but it can be broken down into its constituent elements. Considering this information, Alarcón [28] proposes to study happiness as a multidimensional construct which converges satisfaction of what has been achieved, positive attitudes toward life, (experiences that reflect positive feelings concerning one’s self and life) personal fulfillment, and joy of living.
Happiness Scale of Lima (HSL) [28] , consists of 27 items and reported item-scale correlations were highly significant and high internal consistency (∝ = 0.92). The factorial analysis of principal components and varimax
rotation, revealed that happiness is a multidimensional behavior, consisting of four dimension: 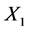 Sense positive of life,
Sense positive of life, 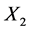 Satisfaction with life,
Satisfaction with life, 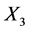 Personal fulfillment and
Personal fulfillment and 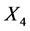 Joy of living.
Joy of living.
2. The Model
Definition 1
The σ-algebra is used for measured definition. A probability measure is a mapping  that assigns a probability
that assigns a probability  to any event, with the properties
to any event, with the properties 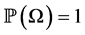 and
and  whenever
whenever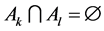 . A real value random variable is a mapping
. A real value random variable is a mapping 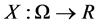 and
and 
Definition 2
A random variables es given by 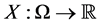 where is measurable and subset of
where is measurable and subset of , we denote by
, we denote by 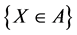 then the event is
then the event is .
.
Definition 3
The random samples, say![]() ,
, ![]() ,
, ![]() y
y![]() , have the same underlying distribution.
, have the same underlying distribution.
We assume that we have four data samples![]() . If the data have the same distributions, then
. If the data have the same distributions, then![]() . Uncertainty about the true value of parameter it described by a measurement conditional observed datasets. The posterior predictive distribution, is defined as
. Uncertainty about the true value of parameter it described by a measurement conditional observed datasets. The posterior predictive distribution, is defined as
![]() (1)
(1)
Lema 1.
Let ![]() be a probability measure on
be a probability measure on ![]() such that
such that
![]()
The probability for ![]() denoted
denoted ![]() is equal to the joint probability
is equal to the joint probability ![]() for any fixed
for any fixed![]() , the probability is bounded by
, the probability is bounded by
![]() (2)
(2)
Consider the problem of selecting independent samples from several populations for the purpose of between-group comparisons, either through hypothesis testing or estimation of mean differences. A companion problem is the estimation of within-group mean levels. Together, these problems form the foundation for the very common analysis of variance framework, but also describe essential aspects of stratified sampling, cluster analysis, empirical Bayes, and other settings. Procedures for making between-group comparisons are known as multiple comparisons methods. The goal of determining which groups have equal means requires testing a collection of related hypotheses [29] .
Consider independent samples from l normally distributed populations with equal variances (3a y 3b)
![]() (3a)
(3a)
![]() (3b)
(3b)
Then ![]() for each
for each ![]() then there is
then there is ![]() tests. For example, for two sample there is 1 test, for three sample there is 3 test, and 4 there is 6 test. When two or more means are taken as equal, we merely combine all relevant samples into one.
tests. For example, for two sample there is 1 test, for three sample there is 3 test, and 4 there is 6 test. When two or more means are taken as equal, we merely combine all relevant samples into one.
Let ![]() denote the observed data. Assume that
denote the observed data. Assume that ![]() is to be described using a model
is to be described using a model ![]() selected from a set of candidate models
selected from a set of candidate models![]() . Assume that each
. Assume that each ![]() is uniquely parameterized by
is uniquely parameterized by![]() , an element of the parameter space
, an element of the parameter space![]() . In the multiple comparisons problem, the class of candidate models consists of all possible mean level clustering. Each candidate model is parameterized by the mean vector
. In the multiple comparisons problem, the class of candidate models consists of all possible mean level clustering. Each candidate model is parameterized by the mean vector ![]() and the common variance
and the common variance![]() , with the individual means restricted by the model defined clustering of equalities. That is, each model determines a corresponding parameter space where particular means are taken as equal.
, with the individual means restricted by the model defined clustering of equalities. That is, each model determines a corresponding parameter space where particular means are taken as equal.
Let![]() , where
, where ![]() take values in a d-dimensional parameter space
take values in a d-dimensional parameter space![]() , be likelihood [30] - [33] functions associated with the samples and
, be likelihood [30] - [33] functions associated with the samples and ![]() denote a prior density on
denote a prior density on ![]() over the model
over the model![]() . Then
. Then ![]() denote a prior on
denote a prior on ![]() given the model
given the model![]() . The posterior probability for
. The posterior probability for ![]() and
and ![]() can be written as
can be written as
![]() (4)
(4)
![]() (5)
(5)
You can write the posterior probability (4) y (5) as,
![]() (6)
(6)
We use a uniform prior for ![]() (6) it can be written as
(6) it can be written as
![]()
![]()
we using equations (5,6) and the previous development, we write the following relationship
![]() (7)
(7)
Definition 4
The Taylor series of a real or complex-valued function ![]() that is infinitely differentiable at a real or complex number is the power series
that is infinitely differentiable at a real or complex number is the power series
![]()
Then, applying the definition 4 to (7), we obtain
![]() (8)
(8)
The Fisher information [30] is a way of measuring the amount of information that an observable random variable X carries out unknown parameter θ.
![]() (9)
(9)
Applying (9) to (8), is obtained
![]()
![]() (10)
(10)
taken
![]()
![]()
Then
![]() (11)
(11)
With respect to the candidate model class![]() , we obtain, the posterior model probabilities
, we obtain, the posterior model probabilities
![]() (12)
(12)
Many clever methods have been devised for constructing and sampling from arbitrary posterior distributions. Markov chain simulation (also called Markov chain Monte Carlo, or MCMC) is a general method based on drawing values of θ from approximate distributions and then correcting those draws to better approximate the
target posterior distribution, ![]() [34] [35] . The sampling is done sequentially, with the distribution of the sampled draws depending on the last value drawn; hence, the draws form a Markov chain. (As defined in probability theory, a Markov chain is a sequence of random variables
[34] [35] . The sampling is done sequentially, with the distribution of the sampled draws depending on the last value drawn; hence, the draws form a Markov chain. (As defined in probability theory, a Markov chain is a sequence of random variables ![]() for which, for any t, the distribution
for which, for any t, the distribution
of ![]() given all previous θ’s depends only on the most recent value) The key to the method’s success, however, is not the Markov property but rather that the approximate distributions are improved at each step in the simulation, in the sense of converging to the target distribution [35] .
given all previous θ’s depends only on the most recent value) The key to the method’s success, however, is not the Markov property but rather that the approximate distributions are improved at each step in the simulation, in the sense of converging to the target distribution [35] .
A z-statistic should be calculated when the standard deviation of the population(s) is known. If the standard deviation is not known, then the standard error must be estimated using the standard deviation of the sample(s). Due to this estimation, we must use the t-distribution which is thicker in the tails to account for estimating the standard error with the sample standard deviation [34] .
![]() (13)
(13)
![]() (14)
(14)
Until now, we have built the theory to apply to the case of four sample data, now what we will do, will be a particular case study, and see that Lema and definitions 1, 2 y 3 are applied naturally like the Equation (14)
Example particular case
Suppose![]() . Select a random sample of size
. Select a random sample of size![]() . From ith group
. From ith group ![]() so sample sizes are
so sample sizes are ![]()
![]()
![]() is the sample mean for the observations in all group combined
is the sample mean for the observations in all group combined
![]()
![]()
Variability in the data, the deviation of an individual observation
![]()
![]()
To test the null hypothesis that the population means are all the same, us the test statistic
![]()
Under![]() , this statistic has t distribution with k-1 and n-k degree freedom.
, this statistic has t distribution with k-1 and n-k degree freedom.
Now four three
Suppose![]() . Select a random sample of size ni. From ith group
. Select a random sample of size ni. From ith group ![]() so sample sizes are
so sample sizes are ![]()
![]()
![]()
![]()
![]()
![]()
Then ![]()
![]()
and
![]()
![]()
The principle of Bayes model is to compute posteriors bases on specified priors and the likelihood function of data, the four groups of size 1110.
We began with a descriptive model of data from four groups, wherein the parameters were meaningful measures of central tendency, variance, and normality. Bayesian inference reallocates credibility to parameter values that are consistent with the observed data. The posterior distribution across the parameter values gives complete information about which combinations of parameter values are credible. In particular, from the posterior distribution we can assess the credibility of specific values of interest, such as zero difference between means, or zero difference between standard deviations. We can also decide whether credible values of the difference of means are practically equivalent to zero, so that we accept the null value for practical purposes.
The Bayesian posterior distribution can also be used as a complete hypothesis for assessing power, that is, the probabilities of achieving research goals such as rejecting a null value, accepting a null value, or reaching a desired precision of estimation. The power estimation incorporates all the information in the posterior distribution by integrating across the credible parameter values, using each parameter-value combination to the extent it is credible. Figure 1 shows histograms of data that are labeled with ![]() on their abscissas, and these data are fixed at their empirically observed values.
on their abscissas, and these data are fixed at their empirically observed values.
3. Bayesian Multiple Linear Regression
![]() now, we need to find an adjustment function for the above data. A linear regression model where more than one variable involved is called multiple regression model [36] - [38]
now, we need to find an adjustment function for the above data. A linear regression model where more than one variable involved is called multiple regression model [36] - [38]
![]() (15)
(15)
where, we have k regressors, parameters ![]() they are regression coefficients, then the Approach Bayesian Multiple Linear Regression is [36] [37]
they are regression coefficients, then the Approach Bayesian Multiple Linear Regression is [36] [37]
![]() (16)
(16)
The prior distribution of ![]() is NIG (Normal-Inverse-Gamma) and it is given by
is NIG (Normal-Inverse-Gamma) and it is given by ![]() thus
thus ![]() they are hyperparameters.
they are hyperparameters.
![]() (17)
(17)
![]()
![]()
![]()
Figure 1. Posterior predictive probability dimensions.
![]()
where IG (Inverse Gaussian)
If we denote by ![]() y
y ![]()
We can express the density function as
![]() (18)
(18)
The conjugate prior distribution will be given by
![]() (19)
(19)
In the scheme MCMC
![]() (20)
(20)
where ![]() is a matrix (n ´ p) and
is a matrix (n ´ p) and ![]() is the covariance matrix and
is the covariance matrix and ![]() is a vector dimension p of regression coefficients to do Bayesian estimation. Assume the prior distribution of
is a vector dimension p of regression coefficients to do Bayesian estimation. Assume the prior distribution of ![]() is
is
![]() (21)
(21)
where ![]() and
and ![]() are matrices representing our beliefs about average and covariance of prior distribution. Take
are matrices representing our beliefs about average and covariance of prior distribution. Take ![]() and using Bayesian approach, we obtain
and using Bayesian approach, we obtain
![]() (22)
(22)
where
![]()
![]()
We can see that both matrices have two terms, one that only it depends on the prior and other that only it depends of data. This is very useful because in each iteration. We have to update only the last term. The question to be dealt is the choice of hyperparameters ![]() y
y ![]()
![]()
![]()
Then, we can write the equation as follows [38]
![]() (23)
(23)
Figures 2-5 show the range HDI, which means Higher Density Interval. Values inside HDI have a greater probability density (credibility) that values outside this. Therefore, the 95% HDI includes the most incredible parameters values. There is a way that the posterior 95% HDI could exclude zero even when the data have a frequency of zero. It can happen if the prior already excludes zero. This interval is useful as a summary of the distribution and decision tool. The decision rule is simple. Any value outside of the 95% HDI is rejected [38] .
In all four cases the focus is on assessing if the predictors were differentially predictive, for which we examine the posterior distribution of the differences standardized regression coefficients, given that the comparison is based in the normalization using the single sample.
As shown in Figure 2, the data to ![]() none of the coefficients are within the supposed. We observed than for X1 (sense positive of life) for differences in
none of the coefficients are within the supposed. We observed than for X1 (sense positive of life) for differences in ![]() are out of interval to be credible, indicating than
are out of interval to be credible, indicating than![]() , cannot be a linear combination of the other dimensions.
, cannot be a linear combination of the other dimensions.
In Figure 4, the outcomes for dataset ![]() where X2 (satisfaction with life)
where X2 (satisfaction with life)![]() ,
,
![]()
Figure 2. Posteriori distribution for X1.
![]()
Figure 3. Posteriori distribution for X2.
![]()
Figure 4. Posteriori distribution for X3.
![]()
Figure 5. Posteriori distribution for X4.
HDI goes from 0.209 to 0.391. Therefore X1 and X3 are equally costly and if we want to avoid double cost of measuring both, then, is probable to be more effective assess X2 than X3.
In Figure 5 the outcomes for dataset![]() , where X3 (personal fulfillment)
, where X3 (personal fulfillment)![]() ,
,
HDI goes from 0.149 to 0.325. Therefore X1 and X2 are equally costly and if we want to avoid double cost of measuring both, then, is probable to be more effective assess X1 than X4.
Figure 5 shows for dataset![]() , where X4 (joy of living)
, where X4 (joy of living)![]() , HDI goes from
, HDI goes from
0.0205 to 0.191. Therefore X1 and X2 are equally costly, and if we want to avoid double cost of measuring both, then, is probable to be more effective assess X1 than X2.
The template is used to format your paper and style the text. All margins, column widths, line spaces, and text fonts are prescribed; please do not alter them. You may note peculiarities. For example, the head margin in this template measures proportionately more than is customary. This measurement and others are deliberate, using specifications that anticipate your paper as one part of the entire journals, and not as an independent document. Please do not revise any of the current designations.
4. Conclusions
Bayesian methods have been developed as a tool for reasoning quantitatively in situations where arguments cannot be made with certainty. The focus recent developments of Markov chain Monte Carlo algorithms, in many situations the only way to integrate over the parameter space. The use of posterior predictive distributions makes the method robust to the choice of priors on the model parameters and enables the use of improper priors even when only very few observations are available. To measure the agreement between posterior predictive distributions, we derive a measure which has an intuitive probabilistic interpretation.
Within the discussion of the results, we found that the sample has not atypical behavior, too, and that suitable modifications can be described through a test. Another interesting result obtained is that the predictive probability for the case of X1 (sense positive of life) and X3 (personal fulfillment) dimensions exhibit a non-uniform variation, while other factors are uniform distribute.
The hypotheses of work, was that if through sample analysis could infer that happiness, only one is affected by three dimensions X2 (sense positive of life), X3 (personal fulfillment) and X4 (satisfaction with life). In this context, we note that the hypothesis was tested, the marked tendency on distributions in recent factors was sufficient to support this theory, on the other hand, through the Multilinear Regression Bayesian, also tested this hypothesis.
Due to recent revolutionary advances in Bayesian posterior computation via computer-intensive MCMC simulation techniques, difficulties with posterior computations can be overcome. A Bayesian state-space model is readily implemented using standard Bayesian software such as JAGS, BUGS, NIMBLE and STAN. One can therefore avoid writing one-off programs in a low-level language. Any modifications, such as different prior distributions, applications to different data sets, or the use of different sampling distributions, require the change of just a single line in the code.
NOTES
![]()
*Corresponding author.