Global Convergence of Curve Search Methods for Unconstrained Optimization ()
Received 20 December 2015; accepted 25 April 2016; published 28 April 2016

1. Introduction
Line search method is an important and mature technique in solving an unconstrained minimization problem
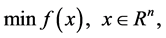 (1)
(1)
where  is an n-dimensional Euclidean space and
is an n-dimensional Euclidean space and 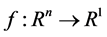 is a continuously differentiable function. It takes the form
is a continuously differentiable function. It takes the form
 (2)
(2)
where  is a descent direction of
is a descent direction of  at
at 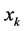 and
and 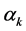 is a step size to satisfy the descent condition
is a step size to satisfy the descent condition
 (3)
(3)
One hopes that 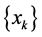 generated by line search method converges to the minimizer
generated by line search method converges to the minimizer 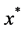 of (1) in some sense. Let
of (1) in some sense. Let  be the current iterate. We denote
be the current iterate. We denote 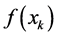 by
by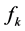 ,
, by
by![]() , and
, and ![]() by
by![]() , respectively.
, respectively.
At the k-th iteration of line search methods, one first chooses a search direction and then seeks a step size along the search direction and completes one iteration (see [1] ). The search direction ![]() is generally required to satisfy
is generally required to satisfy
![]() (4)
(4)
which guarantees that ![]() is a descent direction of
is a descent direction of ![]() at
at ![]() (e.g. [2] [3] ). In order to guarantee the global convergence, we sometimes require
(e.g. [2] [3] ). In order to guarantee the global convergence, we sometimes require ![]() to satisfy the sufficient descent condition
to satisfy the sufficient descent condition
![]() (5)
(5)
where ![]() is a constant. Moreover, the angle testing condition is commonly used in proving the global convergence of related line search methods, that is
is a constant. Moreover, the angle testing condition is commonly used in proving the global convergence of related line search methods, that is
![]() (6)
(6)
where![]() .
.
In line search methods we try to find an ![]() to reduce
to reduce ![]() over the ray
over the ray ![]() at the k- th iteration, while curve search method is to define the next iterate on the curve
at the k- th iteration, while curve search method is to define the next iterate on the curve
![]()
where ![]() and
and ![]() means that
means that ![]() is continuously differentiable on
is continuously differentiable on![]() . It is obvious that line search method is a special one of curve search methods. In other words, curve search method is a generalization of line search methods.
. It is obvious that line search method is a special one of curve search methods. In other words, curve search method is a generalization of line search methods.
McCormick [4] and Israel Zang [5] proposed an arc method for mathematical programming, which is actually a special one of curve search methods. Similarly as in line search methods, how to choose a curve at each iteration is the key to using curve search methods.
Botsaris [6] - [9] studied differential gradient method (abbreviated as ODE method) for unconstrained minimi- zation problems. It is required to solve differential equations at the k-th iteration
![]()
or to solve
![]()
where ![]() and
and ![]() The ODE method has been investigated by many researchers (e.g. [10] - [14] ) and is essentially a curve search method.
The ODE method has been investigated by many researchers (e.g. [10] - [14] ) and is essentially a curve search method.
However, it is required to solve some initial-value problems of ordinary differential equations to define the curves in ODE methods. Some other curve search methods with memory gradient have also been investigated and been proved to be a kind of promising methods for large-scale unconstrained optimization problems (see [15] [16] ). Other literature on curve search methods have appeared in the literature [17] - [19] . To the best of our knowledge, the unified form of curve search methods has rarely been studied in present literature. It is necessary to study the general scheme of curve search methods and its global convergence.
In this paper we present a new family of curve search methods for unconstrained minimization problems and prove their global convergence and linear convergence rate under some mild conditions. These method are based on searching a new iterate along a curve at each iteration, while line search methods are based on finding a new iterate on a line starting from the current iterate at each iteration. Many curve search rules proposed in the paper can guarantee the global convergence and linear convergence rate of these curve search methods. Some implementable version of curve search methods are presented and numerical results show that some curve search methods are stable, useful and efficient in solving large scale minimization problems.
The rest of this paper is organized as follows. In the next section we describe the curve search methods. In Sections 3 and 4 we analyze its global convergence and linear convergence rate respectively. In Section 5 we report some techniques for choosing the curves and conduct some numerical experiments. And finally some conclusion remarks are given in Section 6.
2. Curve Search Method
We first assume that
(H1). The objective function ![]() is continuously differentiable on
is continuously differentiable on ![]() and the level set
and the level set
![]() is bounded, where
is bounded, where ![]() is given.
is given.
(H1'). The gradient ![]() of
of ![]() is Lipschitz continuous on an open bounded convex set B that contains the level set
is Lipschitz continuous on an open bounded convex set B that contains the level set![]() , i.e., there exists
, i.e., there exists ![]() such that
such that
![]()
Definition 2.1. Let ![]() be the current iterate and B be an open bounded convex set that contains
be the current iterate and B be an open bounded convex set that contains![]() . We define a curve within B through
. We define a curve within B through ![]() as follows
as follows
![]()
where ![]() and
and ![]() is continuously differentiable on
is continuously differentiable on ![]() with
with ![]() and
and![]() .
.
Definition 2.2. We call the one-dimensional function ![]() a forcing function if
a forcing function if
![]()
where ![]()
It is obvious that the addition, the multiplication and the composite function of two forcing functions are also forcing functions.
In order to guarantee the global convergence of curve search methods, we suppose that the initial descent direction ![]() and the curve
and the curve ![]() satisfies the following assumption.
satisfies the following assumption.
(H2). The search curve sequence ![]() satisfies
satisfies
![]()
![]()
where ![]() and
and ![]() are forcing functions.
are forcing functions.
Remark 1. In fact, if there exist ![]() and
and ![]() such that
such that ![]() and
and
![]()
where ![]() then the curve sequence
then the curve sequence ![]() satisfies (H2).
satisfies (H2).
This kind of curves are easy to find. For example,
![]()
are curves that satisfy (H2) and so are the following curves
![]()
(for![]() ), provided that
), provided that ![]() and
and ![]() are bounded for all
are bounded for all![]() .
.
Remark 2. If ![]() is twice continuously differentiable and there exist M and
is twice continuously differentiable and there exist M and ![]() such that
such that
![]() and
and ![]() for all
for all![]() , then the curve sequence
, then the curve sequence ![]() satisfies (H2) be-
satisfies (H2) be-
cause of
![]()
and
![]()
Remark 3. In line search methods, if we let ![]() and
and ![]() be bounded for all k, then
be bounded for all k, then ![]() satisfies (H2). As a result, line search method is a special one of curve search methods and its convergence can be derived from the convergence of curve search methods.
satisfies (H2). As a result, line search method is a special one of curve search methods and its convergence can be derived from the convergence of curve search methods.
In the sequel, we describe the curve search method.
Algorithm (A).
Step 0. Choose ![]() and set
and set![]() .
.
Step 1. If ![]() then stop else go to Step 2;
then stop else go to Step 2;
Step 2. Let ![]() be defined by Definition 2.1 and
be defined by Definition 2.1 and ![]() satisfies (4). Set
satisfies (4). Set ![]() where
where ![]() is selected by some curve search rule;
is selected by some curve search rule;
Step 3. Set ![]() and go to Step 1.
and go to Step 1.
Once the initial descent direction ![]() and the search curve
and the search curve ![]() are determined at the k-th iteration, we need to seek a step size
are determined at the k-th iteration, we need to seek a step size ![]() such that
such that
![]()
For convenience, let ![]() satisfy (4). There are several curve search rules as follows.
satisfy (4). There are several curve search rules as follows.
(a) Exact Curve Search Rule. Select an ![]() to satisfy
to satisfy
![]() (7)
(7)
(b) Approximate Exact Curve Search Rule. Select ![]() to satisfy
to satisfy
![]() (8)
(8)
(c) Armijo-type Curve Search Rule. Set![]() ,
, ![]() ,
, ![]() and
and![]() . Choose
. Choose ![]()
to be the largest ![]() in
in ![]() such that
such that
![]() (9)
(9)
(d) Limited Exact Curve Search Rule. Set ![]() and
and![]() . Choose
. Choose ![]() to satisfy
to satisfy
![]() (10)
(10)
(e) Goldstein-type Curve Search Rule. Set ![]() Choose
Choose ![]() to satisfy
to satisfy
![]() (11)
(11)
(f) Strong Wolfe-type Curve Search Rule. Set ![]() and
and![]() . Choose
. Choose ![]() to satisfy simul- taneously
to satisfy simul- taneously
![]() (12)
(12)
and
![]() (13)
(13)
(g) Wolfe-type Curve Search Rule. Set ![]() and
and![]() . Choose
. Choose ![]() to satisfy simultaneously
to satisfy simultaneously
(12) and
![]() (14)
(14)
Lemma 2.1. Let ![]() be defined in Definition 2.1 and
be defined in Definition 2.1 and ![]() satisfies (4). Assumptions (H1) and (H2) hold and let
satisfies (4). Assumptions (H1) and (H2) hold and let![]() . Then
. Then
![]()
where ![]() is a forcing function.
is a forcing function.
Proof. Assumption (H1) and Definition 2.1 imply that ![]() is uniformly continuous on B and thus, there exist
is uniformly continuous on B and thus, there exist ![]() and a forcing function
and a forcing function ![]() such that
such that
![]() (15)
(15)
By (H2), Definition 2.1 and (15), noting that ![]() and
and![]() , we have
, we have
![]()
□
Lemma 2.2. If (H1) holds and ![]() is defined by Definition 2.1 and
is defined by Definition 2.1 and ![]() satisfies (4), then
satisfies (4), then ![]() is well defined in the seven curve search rules.
is well defined in the seven curve search rules.
Proof. Let![]() . Obviously
. Obviously![]() ,
,![]() . The following limit
. The following limit
![]()
implies that there exists ![]() such that
such that
![]()
Thus
![]()
which shows that the curve search rules (a), (b), (c) and (d) are well-defined.
In the following we prove that the curve search rules (e), (f) and (g) are also well-defined.
For the curve search rule (e), (H1) and
![]()
imply that the curve ![]() and the line
and the line ![]() must have an intersection point
must have an intersection point ![]() and thus
and thus
![]()
which shows that the curve search rule (e) is well-defined.
For the curve search rules (f) and (g), (H1) and
![]()
imply that the curve ![]() and the line
and the line ![]() must have an intersection point and suppose that
must have an intersection point and suppose that ![]() is not the origin (0,0) but the nearest intersection point to (0,0). Thus
is not the origin (0,0) but the nearest intersection point to (0,0). Thus
![]() (16)
(16)
and
![]() (17)
(17)
where![]() . Using the mean value theorem, there exists
. Using the mean value theorem, there exists ![]() such that
such that
![]()
By (16) we have
![]()
and thus,
![]()
Therefore,
![]() (18)
(18)
Obviously, it follows from (17) and (18) that ![]() satisfies (12) and (14) (also satisfies (12) and (13)). This shows that the curve search rules (f) and (g) are well-defined.
satisfies (12) and (14) (also satisfies (12) and (13)). This shows that the curve search rules (f) and (g) are well-defined.
□
3. Global Convergence
Theorem 3.1. Assume that (H1), (H1') and (H2) hold, ![]() is defined by Definition 2.1 and
is defined by Definition 2.1 and ![]() satisfies (5) and
satisfies (5) and
![]() (19)
(19)
where ![]() is a constant. If
is a constant. If ![]() is defined by the curve search rules (a), (b), (c) or (d) and Algorithm (A) generates an infinite sequence
is defined by the curve search rules (a), (b), (c) or (d) and Algorithm (A) generates an infinite sequence![]() , then
, then
![]()
Proof. Using reduction to absurdity, suppose that there exist an infinite subset ![]() and an
and an ![]() such that
such that
![]() (20)
(20)
(H1) implies that ![]() has a bound, say
has a bound, say![]() , i.e.,
, i.e., ![]() , and thus
, and thus ![]()
Let
![]()
In the case of![]() , for the curve search rule (c), there must exist
, for the curve search rule (c), there must exist ![]() such that
such that
![]() (21)
(21)
because of
![]()
By (9) and (21) we have
![]()
By (H1) we can obtain
![]()
which contradicts (20).
In the case of![]() , there must exist an infinite subset
, there must exist an infinite subset ![]() such that
such that
![]() (22)
(22)
Therefore, for sufficiently large![]() ,
, ![]() implies that
implies that ![]() and
and
![]()
Using the mean value theorem on the left-hand side of the above inequality, there exists ![]() such that
such that
![]()
and thus
![]()
Hence
![]() (23)
(23)
By (22), (23) and Lemma 2.1, we have
![]()
which also contradicts (20).
In fact, we can prove that ![]() for the curve search rule (c). If
for the curve search rule (c). If ![]() then there exists an infinite subset
then there exists an infinite subset ![]() such that (22) holds and thus, (23) holds. By (19), (5), (H1'), the mean value theorem, (H2) and (22), we have
such that (22) holds and thus, (23) holds. By (19), (5), (H1'), the mean value theorem, (H2) and (22), we have
![]()
This contradiction shows that![]() .
.
For the curve search rules (a), (b) and (d), since ![]() for the curve search rule (c), let
for the curve search rule (c), let ![]() be the step size defined by the three curve search rules (a), (b) and (d), and let
be the step size defined by the three curve search rules (a), (b) and (d), and let ![]() be the step size defined by the curve search rule (c), then we have
be the step size defined by the curve search rule (c), then we have
![]()
This and (H1) imply that
![]()
holds for the curve search rules (a), (b) and (d), which contradicts (20). The conclusion is proved.
□
Theorem 3.2. Assume that (H1) and (H2) hold, ![]() is defined by Definition 2.1 and
is defined by Definition 2.1 and ![]() satisfies (5) and (19),
satisfies (5) and (19), ![]() is defined by the curve search rules (e), (f) or (g). Algorithm (A) generates an infinite sequence
is defined by the curve search rules (e), (f) or (g). Algorithm (A) generates an infinite sequence![]() . Then
. Then
![]()
Proof. Using reduction to absurdity, suppose that there exist an infinite subset ![]() and an
and an ![]() such that (20) holds and let
such that (20) holds and let
![]()
For the curve search rules (e), (f) and (g), in the case of![]() , by (11), (12) and (5), we have
, by (11), (12) and (5), we have
![]()
By (H1) we have
![]()
which contradicts (20).
In the case of![]() , there must exist an infinite subset
, there must exist an infinite subset ![]() such that (22) holds. For the curve search rule (e), by the left-hand side inequality of (11) and using the mean value theorem, there exists
such that (22) holds. For the curve search rule (e), by the left-hand side inequality of (11) and using the mean value theorem, there exists ![]() such that
such that
![]()
Thus
![]() (24)
(24)
By (22), (24) and Lemma 2.1, we have
![]()
which contradicts (20). For the curve search rules (f) and (g), by (14), (22) and Lemma 2.1, we have
![]()
which also contradicts (20).
The conclusions are proved.
□
Corollary 3.1. Assume that (H1), (H1') and (H2) hold, ![]() is defined by Definition 2.1 with
is defined by Definition 2.1 with ![]() satisfying (5) and (19),
satisfying (5) and (19), ![]() is defined by the curve search rules (a), (b), (c), (d), (e), (f) or (g), and Algorithm Model (A) generates an infinite sequence
is defined by the curve search rules (a), (b), (c), (d), (e), (f) or (g), and Algorithm Model (A) generates an infinite sequence![]() . Then
. Then
![]()
Proof. By Theorems 3.1 and 3.2, we can complete the proof.
□
4. Convergence Rate
In order to analyze the convergence rate, we further assume that
(H3). The sequence ![]() generated by curve search method converges to
generated by curve search method converges to![]() ,
, ![]() is a symmetric
is a symmetric
positive definite matrix and ![]() is twice continuously differentiable on
is twice continuously differentiable on![]() , where
, where
![]() .
.
Lemma 4.1. Assume that (H3) holds. Then there exist ![]() and
and ![]() such that
such that
![]() (25)
(25)
![]() (26)
(26)
![]() (27)
(27)
and thus
![]() (28)
(28)
By (28) and (27) we can obtain, from the Cauchy-Schwartz inequality , that
![]() (29)
(29)
and
![]() (30)
(30)
Its proof can be seen from the book ( [3] , Lemma 3.1.4).
Lemma 4.2. Assume that (H2) and (H3) hold and ![]() is defined by Definition 2.1 and
is defined by Definition 2.1 and ![]() satisfies (5) and (19). Algorithm (A) generates an infinite sequence
satisfies (5) and (19). Algorithm (A) generates an infinite sequence![]() . Then there exist
. Then there exist ![]() and
and ![]() such that
such that
![]() (31)
(31)
Proof. We first prove that (31) holds for the curve search rules (c), (e), (f) and (g), and then we can prove (31) also holds for the curve search rules (a), (b) and (d).
By (9), (11), (12) and (5), we have
![]() (32)
(32)
Since![]() , there must exist a
, there must exist a ![]() such that
such that
![]() (33)
(33)
By (4), Cauchy Schwartz inequality and (19), we have
![]() (34)
(34)
Let
![]()
If ![]() then the conclusion is proved. If
then the conclusion is proved. If ![]() there must exist an infinite subset
there must exist an infinite subset ![]() such that
such that
![]()
Letting
![]()
for (23),
![]()
for (24) and
![]()
for (13), we have
![]() (35)
(35)
By (35), (23), (24), (14), (34) and Lemma 2.1, we have
![]()
The contradiction shows that ![]() does not occur and thus
does not occur and thus![]() . By letting
. By letting![]() , where
, where
![]() (36)
(36)
we can obtain the conclusion.
For the curve search rules (a), (b) and (d), let ![]() denote the exact step size and
denote the exact step size and ![]() denote the step size generated by the curve search rule (c). By the previous proof, we have
denote the step size generated by the curve search rule (c). By the previous proof, we have
![]()
All the conclusions are proved.
□
Theorem 4.1. Assume that (H2) and (H3) hold and ![]() is defined by Definition 2.1 and
is defined by Definition 2.1 and ![]() satisfies (5) and (19). Algorithm (A) generates an infinite sequence
satisfies (5) and (19). Algorithm (A) generates an infinite sequence![]() . Then
. Then ![]() converges to
converges to ![]() at least R-linearly.
at least R-linearly.
Proof. By Lemmas 4.1 and 4.2 we obtain
![]()
By setting
![]()
we can prove that ![]() In fact, by the definition of
In fact, by the definition of ![]() in the proof of Lemma 4.2 and (36), we obtain
in the proof of Lemma 4.2 and (36), we obtain
![]()
By setting
![]()
and knowing![]() , we obtain from the above inequality that
, we obtain from the above inequality that
![]()
By Lemma 4.1 and the above inequality we have
![]()
thus
![]()
i.e.,
![]()
Therefore,
![]()
which shows that ![]() converges to
converges to ![]() at least R-linearly.
at least R-linearly.
□
5. Some Implementable Version
5.1. How to Find Curves
In order to find some curves satisfying Definition 2.1 and (H2), we first investigate the slope and curvature of a curve. Given a curve ![]() satisfying
satisfying![]() , if it is twice continuously differentiable, then the slope of the curve at
, if it is twice continuously differentiable, then the slope of the curve at ![]() is
is ![]() and the curvature is
and the curvature is![]() . We hope that the curve is a descent curve at
. We hope that the curve is a descent curve at![]() , i.e.
, i.e.![]() . Generally, we require
. Generally, we require ![]() to satisfy
to satisfy
![]()
where ![]() and
and![]() . Moreover, we expect the curves to satisfy
. Moreover, we expect the curves to satisfy
![]()
It is worthy to point out that many convergence properties of curve search methods remain hold for line search method. In fact, the line ![]() satisfies Definition 2.1 and (H2), provided that
satisfies Definition 2.1 and (H2), provided that ![]() is bounded for
is bounded for ![]() For example, we take
For example, we take ![]() with
with
![]() (37)
(37)
where m is a positive integer and
![]()
We can prove that ![]() satisfies Definition 2.1 and (H2) under some mild conditions. Numerical results showed that the curve search method was more efficient than some line search methods [16] .
satisfies Definition 2.1 and (H2) under some mild conditions. Numerical results showed that the curve search method was more efficient than some line search methods [16] .
Another curve search method is from [15] with the curve defined by ![]() where
where
![]() (38)
(38)
and
![]() (39)
(39)
This curve also satisfies Definition 2.1 and (H2) with ![]() satisfying (5) under certain conditions and has good numerical performance.
satisfying (5) under certain conditions and has good numerical performance.
Moreover, many researchers take
![]()
and ![]() satisfies (4) [20] . Certainly, we can obtain some curves by solving initial problems or boundary- value problems of ordinary differential equations and sometimes by using interpolation technique. Lucidi, Ferris and Roma proposed a curvilinear truncated Newton method which uses the curve
satisfies (4) [20] . Certainly, we can obtain some curves by solving initial problems or boundary- value problems of ordinary differential equations and sometimes by using interpolation technique. Lucidi, Ferris and Roma proposed a curvilinear truncated Newton method which uses the curve
![]()
with ![]() being the quasi-Newton direction and
being the quasi-Newton direction and ![]() being the steepest descent direction. This method also has good numerical performance [18] [19] because it reduces to quasi-Newton method finally and avoids some disadvantages of quasi-Newton method at the initial iterations. We guess that there may be many curve search methods which are superior to line search methods in numerical performance.
being the steepest descent direction. This method also has good numerical performance [18] [19] because it reduces to quasi-Newton method finally and avoids some disadvantages of quasi-Newton method at the initial iterations. We guess that there may be many curve search methods which are superior to line search methods in numerical performance.
For example, if we take ![]() and suppose that
and suppose that ![]() and
and ![]() are uniformly bounded for k, then the following curve
are uniformly bounded for k, then the following curve
![]()
satisfies (H2), provided that ![]() is bounded. In the following we shall test some curve search methods.
is bounded. In the following we shall test some curve search methods.
5.2. Numerical Experiments
In this subsection, some numerical reports are prisented for some implementable curve search methods. First of all, we consider some curve search methods with memory gradients. The first curve search method is based on the curve
![]() (40)
(40)
The second curve search method is to use the curve
![]() (41)
(41)
and the third curve search method searches along the curve at each iteration
![]() (42)
(42)
We use respectively the Armijo curve search rule and the Wolfe curve search rule to the above three curves to find a step size at each step. Test problems 21 - 35 and their initial iterative points are from the literature [21] . For example, Problem 21 stands for the problem 21 in the literature and so on.
In the curve search rules (c) and (g) we set the parameters ![]() and
and![]() . Numerical performance of the three curve search methods is reported in Table 1 and a pair of numbers means that the first number denotes the number of iterations and the second number denotes the number of functional evaluations. “P” stands for problems, n is the dimension of problems and T denotes total CPU time for solving all the 15 problems. We denote A1, A2 and A3 the curve search methods with the curves (40), (41) and (42) respectively. A1(c) and A1(g) means the A1 algorithm with the curve search rule (c) and the A1 algorithm with
. Numerical performance of the three curve search methods is reported in Table 1 and a pair of numbers means that the first number denotes the number of iterations and the second number denotes the number of functional evaluations. “P” stands for problems, n is the dimension of problems and T denotes total CPU time for solving all the 15 problems. We denote A1, A2 and A3 the curve search methods with the curves (40), (41) and (42) respectively. A1(c) and A1(g) means the A1 algorithm with the curve search rule (c) and the A1 algorithm with
![]()
Table 1. Iterations and function evaluations.
the curve search rule (g) respectively, and so on. The stop criteria is
![]()
It is shown in Table 1 that curve search methods with memory gradients converge to the optimal solutions stably and averagely. In addition, curve search methods with the Wolfe curve search rule are superior to the methods with the Armijo curve search rule. This shows that L = 1 seems to be an inadequate choice in the Armijo curve search rule and we can take L variably at each step similarly as in the literature [16] .
Moreover, many line search methods may fail to converge when solving some practical problems, especially when solving large scale problems, while curve search methods with memory gradients always converge stably. From this point of view, we guess that some curve search methods are available and promising for optimization problems.
6. Conclusions
Some curve search methods have good numerical performance and are superior to the line search methods to certain extent. This motivates us to investigate the general convergence properties of these promising methods.
In this paper we presented a class of curve search methods for unconstrained minimization problems and proved its global convergence and convergence rate under some mild conditions. Curve search method is a generalization of line search methods but it has wider choices than line search methods. Several curve search rules were proposed and some approaches to choose the curves were presented. The idea of curve search methods enables us to find some more efficient methods for minimization problems. Furthermore, numerical results showed that some curve search methods were stable, available and efficient in solving some large scale problems.
For the future research, we should investigate more techniques for choosing search curves that contain the information of objective functions and find more curve search rules for the curve search method.