Approximate Analytical Expressions for the Concentrations of Acetate and Methane in the Microbial Electrochemical Cell ()
Received 3 February 2016; accepted 25 April 2016; published 28 April 2016

1. Introduction
Microbial fuel cells (MFC) can be defined as a microbial catalyzed electrochemical system which can facilitate the direct conversion of substrate to electricity through a cascade of redox reactions, especially in the absence of oxygen [1] . The applications of MFC are widespread in different fields including waste water remediation, toxic pollutants/xenobiotics removal, recovery of commercially viable products, sequestration of CO2 harvesting the energy stored in marine sediments, desalination, etc. [1] . Microbial electrochemical cells are recognized as a modern technology to directly utilize bioenergy stored in organic substances, especially in wastewater [2] . Several experiments have been conducted to evaluate MXCs main performance as a current or hydrogen generator fed with different organic matters [3] and [4] . A simple mediator based model with suspended cells was investigated [5] . A simple model with rapid implementation and computations is used to describe the effect of some operational conditions such as temperature and substrate concentration on in the MFC performance [6] . Pinto developed a time-dependent mathematical model with the uniform distribution of bacteria in the anode chamber. Although a number of MFC mathematical models have been developed and discussed. To the best of the knowledge, only one MEC model has been proposed [7] . Yahya modified this model for a fed-batch reactor. It is a multi population mediator-based model developed based on the Bernard’s anaerobic digestion kinetics model [8] . Alavijeh [2] used a variety of approaches to develop the first generalized conduction-based model for MXCs including both MFCs and MECs. It is a one-dimensional spatial distribution and time-dependent model using Bernard’s anaerobic digestion kinetics model and both biofilm and liquid bulk simulation. The purpose of this communication is to derive the analytical expression for acetate and methane concentration using the Adomain decomposition method. We also provide the tabular complication of concentration of acetate with limiting case results (first order and zero order kinetics).
2. Mathematical Formulation of the Problem
Anolyte contains fermentative microorganisms and acetoclastic methanogens. Biofilm contains acetoclastic methanogens and anode respiring bacteria (electrogens). Acetate is produced during fermentation process and then diffuses to the biofilm where electrogens consume it and conduct electrons to the anode surface [2] . The systematic diagram of the model is represented in Figure 1.
The acetate and methane mass transfer equations through the biofilm are described as follows [2] :
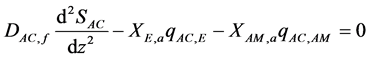 (1)
(1)
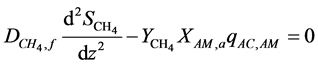 (2)
(2)
![]()
Figure 1. Schematic representation of the model [1] .
where  and
and 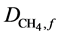 the diffusion coefficient of acetate and methane in the bioflim
the diffusion coefficient of acetate and methane in the bioflim .
.  and
and  are the concentration of acetate on the biofilm
are the concentration of acetate on the biofilm  and methane concentration on the biofilm
and methane concentration on the biofilm .
.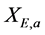 ,
,  and
and 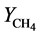 are the density of biomass
are the density of biomass 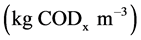 yield coefficient. The acetate consumption rate by electromagnetic microorganism in the biofuel
yield coefficient. The acetate consumption rate by electromagnetic microorganism in the biofuel  is represented by the Nenst-Monoid equation [2]
is represented by the Nenst-Monoid equation [2]
![]() (3)
(3)
where ![]() is the maximum uptake
is the maximum uptake![]() ,
, ![]() are the volume fraction, and Half saturated constant
are the volume fraction, and Half saturated constant![]() .
. ![]() are the Faraday constant, universal gas constant, temperature and local electrical potential of the biofilm respectively. The acetate consumption rate by acetoclastic methangen microorganism in the bioflim
are the Faraday constant, universal gas constant, temperature and local electrical potential of the biofilm respectively. The acetate consumption rate by acetoclastic methangen microorganism in the bioflim ![]() is
is
![]() (4)
(4)
where ![]() and
and ![]() are the volume fraction and Half saturated constant
are the volume fraction and Half saturated constant![]() . At the anode surface, there is no substrate flux and at the surface of the biofilm, there is an interface transfer. The boundary conditions for the above equations are given by [2]
. At the anode surface, there is no substrate flux and at the surface of the biofilm, there is an interface transfer. The boundary conditions for the above equations are given by [2]
![]() (5a)
(5a)
![]() (5b)
(5b)
![]() (5c)
(5c)
![]() (5d)
(5d)
where ![]() represents the space coordinate in the biofilm (m), thickness of the biofilm (m) and boundary layer thickness (m) respectively.
represents the space coordinate in the biofilm (m), thickness of the biofilm (m) and boundary layer thickness (m) respectively. ![]() and
and ![]() are the diffusion coefficient of acetate and methane in the liquid
are the diffusion coefficient of acetate and methane in the liquid![]() .
.![]() is the acetate concentration in the liquid bulk and in the biofilm interface
is the acetate concentration in the liquid bulk and in the biofilm interface
![]() and
and ![]() is the methane concentration in the liquid bulk and in the biofilm interface
is the methane concentration in the liquid bulk and in the biofilm interface![]() . We introduce the following set of dimensionless variables:
. We introduce the following set of dimensionless variables:
![]() (6)
(6)
Using the above dimensionless variables the non-linear reaction-diffusion Equations ((1) and (2)) are expressed in the following dimensionless form:
![]() (7)
(7)
![]() (8)
(8)
The boundary conditions can be written as follows:
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
3. Approximate Analytical Expression of Concentration of Acetate and Methane
Recently, many authors have been applied the Adomain decomposition method (ADM) to various problems and demonstrated the efficiency of the ADM for handling non-linear problem in physics and engineering sciences [9] - [13] . The modified Adomain decomposition method [11] is used to give the approximate solutions of the non-linear Equations ((7) and (8)). Many researchers find that the ADM requires less computational work than traditional approaches [11] - [13] . Other advantages include the ability to solve nonlinear problems without linearization, the wide applicability to several types of problems and scientific fields, and the development of a reliable, analytic solution. Many researchers find that the ADM requires less computational work than traditional approaches [11] - [13] . Other advantages include the ability to solve nonlinear problems without linearization, the wide applicability to several types of problems and scientific fields, and the development of a reliable, analytic solution. Using this method (refer Appendix A), we can obtain the concentrations acetate and methane as follows:
![]() (13)
(13)
![]() (14)
(14)
where the constants
![]() (15)
(15)
Equations ((13) and (14)) are valid provided ![]() and
and![]() . This is the only limitations in this method.
. This is the only limitations in this method.
4. Limiting Case
4.1. Unsaturated (First Order) Catalysis
We initially consider the situation where the concentration of acetate ![]() and methane
and methane ![]() is less than the half saturation constants
is less than the half saturation constants ![]() and
and![]() . In this case
. In this case ![]() Hence, Equations ((7) and (8)) reduces to
Hence, Equations ((7) and (8)) reduces to
![]() (16)
(16)
![]() (17)
(17)
Hence, the non-linear Equations ((7) and (8)) have been reduces to linear equations. Now, the concentration of acetate ![]() and methane
and methane ![]() for corresponding boundary conditions (9a) to (9c) becomes as follows:
for corresponding boundary conditions (9a) to (9c) becomes as follows:
![]() (18)
(18)
![]() (19)
(19)
where ![]() and
and![]() . Equations ((18) and (19)) are the exact solution of Equations ((16) and (17)).
. Equations ((18) and (19)) are the exact solution of Equations ((16) and (17)).
4.2. Saturated (Zero-Order) Catalysis
We now consider that the second major limiting situation found in practice, when the concentration of acetate and methane is very much greater than the half saturation constants ![]() and
and![]() . In this case,
. In this case,![]() . Hence, the non-linear Equations ((7) and (8)) have been reduces to
. Hence, the non-linear Equations ((7) and (8)) have been reduces to
![]() (20)
(20)
![]() (21)
(21)
The above Equations ((17) and (18)) are linear reaction-diffusion equations which are exactly solvable. By solving the above Equations ((17) and (18)), we can obtain the concentration of Acetate (16), and Methane (17).
![]() (22)
(22)
![]() (23)
(23)
Equations ((22) and (23)) are the exact solution of Equations ((20) and (21)).
4.3. Saturated Electrogenic Microorganism and Acetoclastic Methanogens Are Equal (α = β)
In this case, Equations ((7) and (8)) become as follows:
![]() (24)
(24)
![]() (25)
(25)
In this case, the above non-linear equation can be solved using Adomain decomposition method. Now, the concentrations become
![]() (26)
(26)
![]() (27)
(27)
where the constants ![]() to
to ![]() and k are given in Equation (12), when replacing
and k are given in Equation (12), when replacing![]() . Equations ((26) and (27)) are the approximate analytical expression of concentration of acetate and methane.
. Equations ((26) and (27)) are the approximate analytical expression of concentration of acetate and methane.
5. Discussion
Equations ((7) and (8)) represent the general closed-form of analytical expression for the concentrations of acetate and methane for non steady state condition and for various system parameters (potential, saturation parameter of electrogenic microorganism and acetoelastic methanogenes, the diffusion coefficient of acetate, ratio of the thickness of the biofilm and boundary layer). It is of interest to compare the influence of each parameter on the concentration of acetate and methane for various realistic experimental parameters.
Influence of Potential on the Concentration of Acetate. The influence of dimensionless potential on the concentration of the acetate for some experimental values of parameters is shown in Figure 2(a). The microbial activity is strongly dependent on the redox potential of the anode. From this figure it is observed that the concentration of acetate decreases when ![]() increases or potential decreases.
increases or potential decreases.
Influence of Saturation Parameter of Electrogenic Microorganism ![]() and Acetoelastic-Methhano- genes
and Acetoelastic-Methhano- genes ![]() on Concentration of Acetate.-As shown in Figure 2(b) and Figure 2(c), the concentration of
on Concentration of Acetate.-As shown in Figure 2(b) and Figure 2(c), the concentration of
acetate increases when saturation parameter of electrogenic microrganism ![]() or bulk concentration of the acetate increases and saturation parameter of acetoelastic methanogenes
or bulk concentration of the acetate increases and saturation parameter of acetoelastic methanogenes ![]() decreases. From Figure 2(c) it is also observed that the concentration of acetate is inversely proportional to diffusion coefficient of acetate.
decreases. From Figure 2(c) it is also observed that the concentration of acetate is inversely proportional to diffusion coefficient of acetate.
Influnce of the Ratio of Thickness of the Biofilm and the Boundary Layer. Figure 2(d) represents the concentration verses distance from the anode surface for various values of ![]() or ratio of biofilm thickness and boundary layer thickness
or ratio of biofilm thickness and boundary layer thickness![]() . From this figure, it is inferred that the concentration of acetate increases when the ratio of thickness increases.
. From this figure, it is inferred that the concentration of acetate increases when the ratio of thickness increases.
Influence of Other Parameters of the Concentration of Methane and Acetate. The concentration of methane versus dimensionless distance x for various experimental values of parameters is plotted in Figure 3. From these figure, it is interfered that the concentration of methane increases when ![]() increases or
increases or ![]() decreases.
decreases.
Figure 4 represents the dimensionless concentrations of acetate versus potential for various values of ![]() and
and![]() . From these figures, it is observed that the concentration of acetate increases when thickness
. From these figures, it is observed that the concentration of acetate increases when thickness ![]() and
and ![]() decreases. From Figure 4(d), it is observed that the concentration of acetate does not differ significantly about the parameter
decreases. From Figure 4(d), it is observed that the concentration of acetate does not differ significantly about the parameter![]() .
.
6. Comparison with Numerical Data and Limiting Case Results
The non-linear differential Equations ((9) and (10)) for the given initial-boundary conditions are being solved numerically. The function pdex, in Matlab software which is a function of solving the initial-boundary value problems for non-linear ordinary differential equations is used to solve this equation. Its numerical solution is compared with analytical results in Table 1. The maximum relative error between our analytical result and the numerical result is 0.32%. The Matlab program is also given in Appendix C. The concentration of acetate and methane are also obtained for the following limiting cases, that is zero order kinetics, first order kinetics and saturated electrogenic microorganism and saturated acetoclastic methanogens are equal![]() . Also our analytical results are compared with limiting case results in Figure 5 and it gives a satisfactory agreement.
. Also our analytical results are compared with limiting case results in Figure 5 and it gives a satisfactory agreement.
7. Determination of Kinetic Parameters KAC,E, qAC,AM,max, φE,a, α and β
The acetate consumption rate by electromagnetic microorganism in the microbial fuel cell (Equation (3)) can be written as follows:
![]() (28)
(28)
As shown in Figure 6, ![]() is plotted against
is plotted against ![]() to obtain the straight line with the slope
to obtain the straight line with the slope ![]() and intercept
and intercept![]() . The slope and intercept yields the value of the parameters
. The slope and intercept yields the value of the parameters ![]() and
and![]() .
.
From Equation (10), we can obtain the concentration of acetate at bioflim and anode interface as
![]() (29)
(29)
Now the plot of ![]() versus
versus ![]() gives the slope
gives the slope ![]() and intercept
and intercept![]() . From these plot, we can obtain the kinetic constant
. From these plot, we can obtain the kinetic constant ![]() and
and ![]() (Table 2).
(Table 2).
![]()
Figure 6. Estimation of kinetic parameters ![]() and
and ![]() from Equation (28).
from Equation (28).
8. Conclusion
A theoretical model describing the bio energy production using microbial electrochemical cell via Nernst-Mo- noid kinetics is analyzed. The time independent non-linear partial differential equations have been solved analytically using the Adomain decomposition method. The primary result of this work is the approximate analytical expression of concentration of acetate and methane for all values of parameters. The influence of potential, ratio of thickness of biofilm and boundary layer, etc. on the concentration of acetate and methane is discussed. Our results are in excellent agreement with stimulation and limiting case results. Also two graphical procedures are suggested for estimating the kinetic parameters.
Acknowledgements
This work was supported by the DST SB/SI/PC-50/2012, New Delhi, India. The authors are thankful to Mr. S. Mohamed Jaleel, The Chairman, Dr. A. Senthilkumar, The Principal, Dr. P. G. Jansi Rani, Head of the Department of Mathematics, SethuInistitute of Technology, Kariapatti-626115, Tamilnadu, India for their encouragement.
Appendix A: Basic Concept of the Adomain Decomposition Method
This is given in the supplementary material of the manuscript.
Appendix B: Approximate Analytical Solution of Non Linear Equation (7) Using ADM
In this appendix, we indicate how Equation (6) in this paper is derived. Furthermore, an ADM is constructed to determine the solution of Equation (4) in the operator form,
![]() (B.1)
(B.1)
where![]() . Applying the inverse operator
. Applying the inverse operator ![]() on both sides of Equation (B.1) yields
on both sides of Equation (B.1) yields
![]() (B.2)
(B.2)
where A and B are the constants of integration. We let,
![]() (B.3)
(B.3)
![]() (B.4)
(B.4)
where
![]() (B.5)
(B.5)
From Equations ((B.3) to (B.5)), Equation (B.2) becomes
![]() (B.6)
(B.6)
We identify the zeroth component as
![]() (B.7)
(B.7)
and the remaining components as the recurrence relation
![]() (B.8)
(B.8)
where ![]() are the Adomain polynomials of
are the Adomain polynomials of![]() .We can find the first two
.We can find the first two ![]() as follows:
as follows:
![]() (B.9)
(B.9)
![]() (B.10)
(B.10)
Adding (B.9) and (B.10), we can obtain the concentration of acetate as described in Equation (10) in the text. By substituting the values of ![]() in Equation (8), we get the concentration of the methane (Equation (11)) in the text.
in Equation (8), we get the concentration of the methane (Equation (11)) in the text.
Appendix C: Scilab/Matlab Program for the Numerical Solution of Equation
This is given in the supplementary material of the manuscript.
Supplementary Material of the Manuscript
Appendix A: Basic Concept of the Modified Adomain Decomposition Method
Consider the singular boundary value problem of ![]() order nonlinear differential equation in the form
order nonlinear differential equation in the form
![]() (A.1)
(A.1)
where N is a non-linear differential operator of order less than n, ![]() is given function and
is given function and ![]() are given constants. We propose the new differential operator, as below
are given constants. We propose the new differential operator, as below
![]() (A.2)
(A.2)
where![]() , so, the problem can be written as
, so, the problem can be written as
![]() (A.3)
(A.3)
The inverse operator ![]() is therefore considered a
is therefore considered a ![]() fold integral operator, as below [11] [12]
fold integral operator, as below [11] [12]
![]() (A.4)
(A.4)
By applying ![]() on (A.3), we have
on (A.3), we have
![]() (A.5)
(A.5)
Such that
![]()
The Adomian decomposition method introduce the solution ![]() and the nonlinear function
and the nonlinear function ![]() by infinite series
by infinite series
![]() (A.6)
(A.6)
and
![]() (A.7)
(A.7)
where the components ![]() of the solution
of the solution ![]() will be determined recurrently. Specific algorithms were seen in [11] [12] to formulate Adomian polynomials. The following algorithm:
will be determined recurrently. Specific algorithms were seen in [11] [12] to formulate Adomian polynomials. The following algorithm:
![]() (A.8)
(A.8)
can be used constant Adomian polynomials, when ![]() is a nonlinear function. By substituting (A.6) and (A.7) in to (A.5)
is a nonlinear function. By substituting (A.6) and (A.7) in to (A.5)
![]() (A.9)
(A.9)
Through using modified Adomian decomposition method, the components ![]() can be determined as
can be determined as
![]() (A.10)
(A.10)
which gives
![]() (A.11)
(A.11)
From (A.8) and (A.11), we can determine the components![]() , and hence the series solution of
, and hence the series solution of ![]() in (A.6) can be immediately obtained. For numerical purposes, the n-term approximate
in (A.6) can be immediately obtained. For numerical purposes, the n-term approximate
![]() (A.12)
(A.12)
can be used to approximate the exact solution. The approach presented above can be validated by testing it on a variety of several linear and nonlinear initial value problems.
Appendix C
Scilab/MatlabProgram for the Numerical Solution of Equation (4)
function pdex4
m = 0;
x = linspace (0, 1);
t = linspace (0, 100000);
sol = pdepe(m,@pdex4pde,@pdex4ic,@pdex4bc,x,t);
u1 = sol(:,:,1);
%――――――――――――――――――――?
Figure
plot(x,u1(end,:))
title('u1(x,t)')
xlabel('Distance x')
ylabel('u1(x,1)')
function [c,f,s] = pdex4pde(x,t,u,DuDx)
c =1;
f =1.* DuDx;
e=0.3;alpha=2;
F =-(e*u(1))/((1+(alpha*u(1))));
s =F;
% ――――――――――――――――――――?
function u0 = pdex4ic(x);
u0 = [0];
% ――――――――――――――――――――?
function [pl,ql,pr,qr] = pdex4bc(xl,ul,xr,ur,t)
j=10;
pl = [0];
ql = [1];
pr = [-j*(1-ur(1))];
qr = [1];
NOTES
![]()
*Corresponding author.