Rate Adaptation for Decoding-and-Forward Relay Channel by Random Projections Codes ()
Received 20 February 2016; accepted 24 April 2016; published 27 April 2016

1. Introduction
Rate adaptation is an important issue in wireless communication system. Traditional rate adaptation techniques implemented at transmitter, such as hybrid automatic repeat request (HARQ) and adaptive modulation and coding (AMC), have two defects. The first one is that it is always difficult to estimate channel state information (CSI) accurately, because the channel may vary drastically during several data packets transmission. The other one is that the transmission rate can be adjusted among limited modulation coding schemes (MCS), the coarse granularity of MCS results in a staircase of spectrum efficiency. To solve the two problems mentioned above, three new schemes [1] - [3] have proposed for smooth rate adaption, and all of them implement rate adaptation at receiver and attain continuous spectrum efficiency. Random projection codes (RPC) [3] [4] is a promising technique to implement rate adaption at receiver in modern wireless communication system.
Relay is a new distributed space and time diversity technology. To improve system performance, relay system makes use of the broadcast feature of wireless communications. And it enhances energy efficient and enlarge transmitting range by multi-user’s collaboration. Furthermore, under the condition of no CSI, relay system can adaptively modulate and transmit data by using rateless code. Tian et al. [5] have proposed a novel encode method of rateless code to resolve the error floor problem of LT code [6] for wireless relay networks. based on decode-and-forward (DF) and compress-and-forward protocols, Chen et al. [7] have proposed a full-duplex adaptive relaying scheme by using Raptor codes [8] . Reference [9] - [11] have investigated distributed LT codes, and analyze the asymptotic performance of their proposed distributed coding schemes. Yue et al. [12] [13] have proposed raptor-based distributed network codes scheme, and have given the derivation of upper and lower bit error rate (BER) for their proposed scheme.
However, these schemes and their analysis are all based on LT codes or raptor codes. This paper investigates the rate adaptation schemes based on random projections codes for decoding-and-forward (DF) relay system. We consider classic three node relay system model [14] . In this system model, relay node performs on half- duplex mode. The communication channel is divided broadcast channel and forward channel. Source node uses random projections matrix (RPM)  to encode, and broadcasts progressively modulation symbols to relay node and destination node. In forward mode, relay node uses RPM
to encode, and broadcasts progressively modulation symbols to relay node and destination node. In forward mode, relay node uses RPM 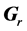 to encode, and forwards progressively modulation symbols to destination node. Destination node will joint decoding after receiving signals from source node or relay node. If decoding successfully, destination node will feedback ACK to source node and relay node, and prepare for transmission of next data frame. Otherwise, it will receive successive signals.
to encode, and forwards progressively modulation symbols to destination node. Destination node will joint decoding after receiving signals from source node or relay node. If decoding successfully, destination node will feedback ACK to source node and relay node, and prepare for transmission of next data frame. Otherwise, it will receive successive signals.
How to design relay schemes is a critical problem. This paper proposes receiving diversity scheme and coding diversity scheme, and presents the joint decoding methods. Furthermore, we discuss the system performance of two relay schemes with different power allocation coefficients. Simulations show that the most power allocation coefficients achieve different gain with the help of relay node. We should allocate power to source node to just guarantee relay node decoding successfully, and allocate remain power to relay node as far as possible. In this way, this DF relay system not only achieves diversity gain, but also achieves higher and smooth spectrum efficiency.
The rest of this paper is organized as follows. Section 2 briefly reviews RPC and its standard decoding algorithm. Section 3 presents the classic relay system model of three nodes, and collaboration scheme based on RPC. Section 4 proposes the decoding and forward relay schemes. The simulation evaluations are included in Section 5. Finally, Section 6 concludes this paper with some discussions on future work.
2. Introduce to Random Projections Codes
In this section, we review the RPC [4] and present the decoding algorithm.
2.1. RPC Encoding
A bipartite graph representation of RPC encoding is provided in Figure 1. Red square and blue circle denote symbol nodes and variable nodes, respectively. Each edge is assigned with a weight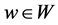 , where
, where
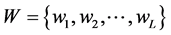 is a vector of real number with length L. The bipartite graph can be represented by
is a vector of real number with length L. The bipartite graph can be represented by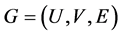 , where
, where 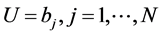 is the set of bits,
is the set of bits, 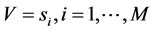 is the set of measurements representing modulated symbols, and E defines the connection between the two sets. In RPC encode, the signal entries are binary. Each coded symbol is calculated by
is the set of measurements representing modulated symbols, and E defines the connection between the two sets. In RPC encode, the signal entries are binary. Each coded symbol is calculated by
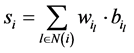 (1)
(1)
where 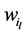 is the weight corresponding to
is the weight corresponding to 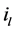 -th bit
-th bit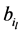 ,
,  denotes the set of neighbors of i-th variable or symbol node. The RPC encoding process can be described by
denotes the set of neighbors of i-th variable or symbol node. The RPC encoding process can be described by
 (2)
(2)
where  is a RPM with
is a RPM with![]() ,
, ![]() is a bits block with length N,
is a bits block with length N, ![]() is the RPC encoded symbols vector with length M.
is the RPC encoded symbols vector with length M.
In order to make use of two dimensional modulation, two consecutive symbols are combined together to form In-phase and Quadrature-phase (IQ) modulation symbol, i.e.,![]() .
.
2.2. RPC Decoding
RPC decoding algorithm uses belief propagation algorithm which is different from LDPC [15] [16] . Since RPC is employing weighted sum check, probability convolution operation is used in horizontal iteration instead of
![]() operation in LDPC. The decoding algorithm of RPC scheme is depicted as factor graph shown in
operation in LDPC. The decoding algorithm of RPC scheme is depicted as factor graph shown in
Figure 1. The edges with a weight ![]() denotes the connections between variable nodes and corresponding
denotes the connections between variable nodes and corresponding
symbol nodes, arrow line denotes the probability message flow. ![]() defines the probability message from the i-th symbol node to the j-th variable node in the t-th iteration.
defines the probability message from the i-th symbol node to the j-th variable node in the t-th iteration. ![]() defines the probability message from the j-th variable node to the i-th symbol node in the (t + 1)-th iteration. The probability message
defines the probability message from the j-th variable node to the i-th symbol node in the (t + 1)-th iteration. The probability message ![]() is computed by the multiplication of probability values
is computed by the multiplication of probability values![]() , from all its neighbors excluding the i-th symbol node. Similarly, the probability message
, from all its neighbors excluding the i-th symbol node. Similarly, the probability message ![]() is given by the convolution of the channel priori probability and all probability values
is given by the convolution of the channel priori probability and all probability values![]() , from its neighbors except j-th variable node. The RPC decoding algo-
, from its neighbors except j-th variable node. The RPC decoding algo-
rithm include initialization, horizontal processing, vertical processing and decision steps. Audience interested in the RPC decoding algorithm are referred to reference [4] .
In summary, RPC is a linear code with rateless characteristics like LT codes. It is obvious that RPC can generate infinity symbols when the row number of ![]() is infinity. RPC adopts weighted sum to check received symbol rather than odd even parity used in LT codes and LDPC. RPC decoding reuses the framework of sum product algorithm for LDPC, but probability convolution operation is used in horizontal iteration instead of
is infinity. RPC adopts weighted sum to check received symbol rather than odd even parity used in LT codes and LDPC. RPC decoding reuses the framework of sum product algorithm for LDPC, but probability convolution operation is used in horizontal iteration instead of ![]() operation. The obvious difference is that RPC combines channel coding and modulation together, and aims to implement rate adaption. In contrast, LDPC is only channel coding scheme.
operation. The obvious difference is that RPC combines channel coding and modulation together, and aims to implement rate adaption. In contrast, LDPC is only channel coding scheme.
3. System Model
3.1. Channel Model
We consider the Gaussian relay system model shown in Figure 2. This system model includes three nodes, i.e., source node denoted as S, relay node denoted as R, and destination node denoted as D. There are three channel links, i.e., SD link, SR link and RD link. The distance between the source node and the destination node is normalized to 1, d denotes the distance between the source node and the relay node, and (1-d) denotes the distance between the relay node and the destination node. Here, we set d = 0.5 and channel fading factor![]() . Then, The corresponding channel gains of SD, SR and RD link are
. Then, The corresponding channel gains of SD, SR and RD link are![]() ,
, ![]() and
and![]() , respectively.
, respectively.
Assuming that the relay node R performs in half duplex mode, the relay channel is divided into broadcast mode (BC) and forward mode (FM). If ![]() denotes the time slot of BC mode, then
denotes the time slot of BC mode, then ![]() is the time slot of FM mode. In BC mode, source node S transmits signals
is the time slot of FM mode. In BC mode, source node S transmits signals ![]() in t time slot. The received signals at relay node R and destination node D are
in t time slot. The received signals at relay node R and destination node D are
![]()
Figure 2. System model of DF relay channel.
![]() (3)
(3)
and
![]() (4)
(4)
respectively. Here, ![]() and
and ![]() are the AWGN noise in R and D, respectively.
are the AWGN noise in R and D, respectively.
After BC transmitting, relay node R starts decoding based on![]() . If successfully decoding, R re-encodes and modulates signals for D in FM mode. Otherwise, R keeps silence. Such that D may receives signals from R.
. If successfully decoding, R re-encodes and modulates signals for D in FM mode. Otherwise, R keeps silence. Such that D may receives signals from R.
![]() (5)
(5)
where ![]() is the modulation signals in relay node R, and
is the modulation signals in relay node R, and ![]() is the AWGN noise at destination node D in FM mode.
is the AWGN noise at destination node D in FM mode.
We define the random variables of![]() ,
, ![]() and
and ![]() are
are![]() ,
, ![]() and
and![]() , respectively. And, we let the powers of
, respectively. And, we let the powers of![]() ,
, ![]() and
and ![]() are unit energy. We define the random variable of
are unit energy. We define the random variable of ![]() is
is![]() , and the random variable of
, and the random variable of ![]() is
is![]() . So, system resource can be characterized by total power P.
. So, system resource can be characterized by total power P. ![]() denotes average symbols energy of
denotes average symbols energy of![]() ,
, ![]() denotes average symbols energy of
denotes average symbols energy of![]() . The constraint of transmitting power at S and R are
. The constraint of transmitting power at S and R are
![]() (6)
(6)
and
![]() (7)
(7)
respectively. Furthermore, system resource allocation is under constraint of inequality (8).
![]() (8)
(8)
3.2. Collaboration Scheme Based on RPC
We assume that source node S uses RPM G1 to encode in BC mode, and relay node R uses RPM Gr to encode in FM mode. Let ![]() denotes the bits block at resource node S. We use the method proposed in [17] to construct RPM. To ensure power of transmitting symbols match the transmission power, we introduce two scaling parameters
denotes the bits block at resource node S. We use the method proposed in [17] to construct RPM. To ensure power of transmitting symbols match the transmission power, we introduce two scaling parameters ![]() and
and ![]() corresponding to
corresponding to ![]() and
and![]() , respectively. Equation (3) can be rewritten by
, respectively. Equation (3) can be rewritten by
![]() . (9)
. (9)
If relay node R participates in collaboration communications, Equations (4) and (5) can be changed as
![]() . (10)
. (10)
Otherwise, destination node D starts decode by using received signals ![]() in BC mode.
in BC mode.
To implement rate adaptation in DF relay system, we propose following communication protocol. Assuming that source node S can completely synchronize with relay node R. Given a SNR, source node S first broadcasts ![]() modulation symbols. Then, S broadcasts progressively
modulation symbols. Then, S broadcasts progressively ![]() modulations symbols in the subsequent time
modulations symbols in the subsequent time
slots. After the first successfully decoding, relay node R transmits ![]() modulation symbols in the first FD mode. Here, l is the number of transmitting progressively. Then, relay node R forwards progressively
modulation symbols in the first FD mode. Here, l is the number of transmitting progressively. Then, relay node R forwards progressively ![]()
modulation symbols to destination node D at subsequent FD mode. Destination node D starts decoding after receiving all the symbols from relay node and source node. If successfully decoding, destination node will feedback ACK to source node S and relay node R. And, source node S and relay node R will transmit next bits block. Otherwise, source node S and relay node R continue progressively transmit modulation symbols.
4. Decoding-and-Forward Scheme
It is important that how to design relay schemes according to two random projections matrix G1 and Gr. In this section, we discuss two schemes as following.
4.1. Receiving Diversity Scheme
In this scheme, we let![]() . The modulation symbols of source node S in BC mode are the same as modulation symbols of relay node R in FM mode, i.e.,
. The modulation symbols of source node S in BC mode are the same as modulation symbols of relay node R in FM mode, i.e.,![]() . There are two cases should be discussed according to whether relay node R forward information to destination node D.
. There are two cases should be discussed according to whether relay node R forward information to destination node D.
The first case is that relay node R has participated in collaboration communication. Destination node D receives two signal vectors with the same symbols and different noise. After simple deformation, Equation (10) can be written as
![]() . (11)
. (11)
where![]() ,
,![]() . The standard variance of
. The standard variance of ![]() and
and ![]() are
are ![]() and
and![]() , respectively. Furthermore, we can use maximum ratio combining (MRC) to reduce channel noise, and get
, respectively. Furthermore, we can use maximum ratio combining (MRC) to reduce channel noise, and get
![]() (12)
(12)
and
![]() . (13)
. (13)
The second case is that destination node D only receives signals ![]() from source node S.
from source node S.
Finally, Destination node D can get the estimation of bits block ![]() by calling the standard decoding algorithm of RPC and RPM
by calling the standard decoding algorithm of RPC and RPM![]() .
.
4.2. Coding Diversity Scheme
In this scheme, we set![]() . The modulation symbols transmitted by source node S in BC mode are different with the modulation symbols sent by relay node R in FM mode, i.e.,
. The modulation symbols transmitted by source node S in BC mode are different with the modulation symbols sent by relay node R in FM mode, i.e.,![]() . Like receiving diversity scheme, we also discuss two case as following.
. Like receiving diversity scheme, we also discuss two case as following.
If relay node R has participated in collaboration communication, the received signals in destination node D are
![]() (14)
(14)
where![]() ,
,![]() . Since
. Since![]() , destination node D needs find linear equation (14). Here, the SNR of
, destination node D needs find linear equation (14). Here, the SNR of ![]() is
is![]() , and the SNR of
, and the SNR of ![]() is
is![]() . In this case, we can’t use directly RPC decoding algorithm to estimate bits block
. In this case, we can’t use directly RPC decoding algorithm to estimate bits block![]() . We need modify two place in decoding algorithm. The first one is that we let
. We need modify two place in decoding algorithm. The first one is that we let![]() , and make use of G to estimate bits block
, and make use of G to estimate bits block![]() . The another one is that we use
. The another one is that we use ![]() to
to
perform noise probability convolution when horizontal iteration in![]() , and use
, and use ![]() to perform noise probability convolution when horizontal iteration in
to perform noise probability convolution when horizontal iteration in![]() .
.
If relay node R isn’t participate in communication, destination node D only receives signals![]() . In this case, we can call directly RPC decoding algorithm to estimate bits block
. In this case, we can call directly RPC decoding algorithm to estimate bits block![]() .
.
5. Simulations
In this section, we evaluate our proposed schemes by BER and capacity metrics in simulations. ![]() denotes the proportion that
denotes the proportion that ![]() accounted for the total power P,
accounted for the total power P, ![]() denotes the proportion that
denotes the proportion that ![]() accounted for the total power P. And it must satisfy the condition
accounted for the total power P. And it must satisfy the condition![]() . Because it is hard to find the closed-form of BER, we analyze the influence that power allocation to relay schemes by running simulations. Table 1 gives out seven pairs of power allocation coefficients. In simulations, we choose
. Because it is hard to find the closed-form of BER, we analyze the influence that power allocation to relay schemes by running simulations. Table 1 gives out seven pairs of power allocation coefficients. In simulations, we choose ![]() as weight set, and use the method proposed in [17] to construct RPM.
as weight set, and use the method proposed in [17] to construct RPM.
5.1. Comparison of BER Performance
In BER simulations, we set the length of bits block N = 400, rate is 1bps, and SNR range is from 5 dB to 15 dB. Figure 3 and Figure 4 describe the BER performance comparison among different power allocation coefficients in receiving diversity scheme and coding diversity scheme, respectively. From this two figures, we can observe
![]()
Figure 3. BER performance comparison among different power allocation coefficients in receiving diversity scheme.
![]()
Figure 4. BER performance comparison among different power allocation coefficients in coding diversity scheme.
![]()
Table 1. Power allocation coefficients.
two interesting points. The first one is that most power allocation coefficients achieve different gain compare to the BER performance of original SD direct link. And, the gain is larger with ![]() increasing in low SNR range. The reason is that the probability of decoding successfully at relay node is low, and the power allocated to source node decides the performance of relay system. Contrarily, the gain is larger with
increasing in low SNR range. The reason is that the probability of decoding successfully at relay node is low, and the power allocated to source node decides the performance of relay system. Contrarily, the gain is larger with ![]() increasing in high SNR range. With the increasing of SNR, the probability of decoding successfully at relay node is enhanced, and the more power allocated to relay node can help destination node decoding. But, when
increasing in high SNR range. With the increasing of SNR, the probability of decoding successfully at relay node is enhanced, and the more power allocated to relay node can help destination node decoding. But, when ![]() equals to 0.2 or 0.3, the BER performance of relay schemes are lower than original SD direct link in all SNR range. The reason is that relay node can’t decoding successfully and the power allocated to relay node is too high. This results in the waste of power.
equals to 0.2 or 0.3, the BER performance of relay schemes are lower than original SD direct link in all SNR range. The reason is that relay node can’t decoding successfully and the power allocated to relay node is too high. This results in the waste of power.
Figure 5 describes the BER performance comparison between receiving diversity and coding diversity with the same of power allocation coefficients. From these figures, we can't observe which relay scheme achieves better performance than other. The reason is that the rate is 1bps, it is not enough to distinguish whose BER performance is better.
5.2. Comparison of Capacity Performance
In capacity simulations, we set the length of bits block N = 400. To implement rata adaptation, we stack a RPM with ![]() four times to form a bigger RPM with
four times to form a bigger RPM with![]() . The number of transmitting progressively equals to 10. The SNR range is from 5 dB to 30 dB, and we run 1000 data frames in each SNR. We first compare the capacity performance between RPC and AMC schemes of IEEE 802.11a, as shown in Figure 6. RPC attains continuous and smooth spectrum efficiency, and its capacity performance is better than that of AMC. Then, we present the capacity performance comparison of our proposed schemes. Figure 7 and Figure 8 show the capacity performance comparison among different power allocation coefficient in receiving diversity scheme and coding diversity scheme, respectively.
. The number of transmitting progressively equals to 10. The SNR range is from 5 dB to 30 dB, and we run 1000 data frames in each SNR. We first compare the capacity performance between RPC and AMC schemes of IEEE 802.11a, as shown in Figure 6. RPC attains continuous and smooth spectrum efficiency, and its capacity performance is better than that of AMC. Then, we present the capacity performance comparison of our proposed schemes. Figure 7 and Figure 8 show the capacity performance comparison among different power allocation coefficient in receiving diversity scheme and coding diversity scheme, respectively.
![]() (a) (b) (c)
(a) (b) (c)![]() (d) (e) (f)
(d) (e) (f)
Figure 5. BER performance comparison between receiving diversity scheme and coding diversity scheme with different power allocation coefficients. (a) β1 = 0.2, βr = 0.8; (b) β1 = 0.3, βr = 0.7; (c) β1 = 0.4, βr = 0.6; (d) β1 = 0.8, βr = 0.2; (e) β1 = 0.7, βr = 0.3; (f) β1 = 0.6, βr = 0.4.
![]()
Figure 6. Capacity performance comparison between RPC and AMC schemes of IEEE 802.11a.
![]()
Figure 7. Capacity performance comparison in receiving diversity scheme.
![]()
Figure 8. Capacity performance comparison in coding diversity scheme.
From Figure 7, we can observe three interesting points. The first one is that most power allocation coeffi-
cients can achieve different gain with the help of relay node, except![]() . The highest capacity of relay system of
. The highest capacity of relay system of ![]() reaches 7.18 bits/symbols/Hz, while SD direct link only reaches 6.63
reaches 7.18 bits/symbols/Hz, while SD direct link only reaches 6.63
bits/symbols/Hz. The maximum gain of relay system is 1.07 bits/symbols/Hz at SNR = 22 dB, the minimum gain of relay system is 0.38 bits/symbols/Hz at SNR = 6 dB. The second one is that capacity performance gains are larger with ![]() increasing in low SNR range. The third one is that the capacity performance relates to the pro-
increasing in low SNR range. The third one is that the capacity performance relates to the pro-
portion of ![]() and
and![]() . The capacity performance curve of
. The capacity performance curve of ![]() can verify this point. It first crosses with the performance curve of
can verify this point. It first crosses with the performance curve of ![]() at SNR = 26 dB. And it is under the performance curve of
at SNR = 26 dB. And it is under the performance curve of ![]() when SNR> 26 dB. This phenomenon illustrates that
when SNR> 26 dB. This phenomenon illustrates that ![]() just satisfies the condition of decoding successfully of relay node at SNR = 26 dB, and the rest of power is allocated to relay node. While
just satisfies the condition of decoding successfully of relay node at SNR = 26 dB, and the rest of power is allocated to relay node. While ![]() wastes energy because of source node with too much energy.
wastes energy because of source node with too much energy.
From Figure 8, we also observe similar features as receiving diversity. Firstly, compare to the SD direct link, the power allocation coefficients, except ![]() and
and![]() , achieve different capacity gain with the help of relay node. The highest capacity of
, achieve different capacity gain with the help of relay node. The highest capacity of ![]() reaches 7.21 bits/symbols/
reaches 7.21 bits/symbols/
Hz. Secondly, in low SNR range, the capacity gains are larger with the ![]() increasing. Thirdly, with the SNR increasing, capacity is not only relate to the proportions of
increasing. Thirdly, with the SNR increasing, capacity is not only relate to the proportions of ![]() and
and![]() , but also relate to the relay schemes.
, but also relate to the relay schemes.
We find that![]() ,
, ![]() and
and ![]() have outstanding performance in low SNR range, and their capacity performance less than others in high SNR range.
have outstanding performance in low SNR range, and their capacity performance less than others in high SNR range.
Figure 9 shows the capacity comparison between receiving diversity scheme and coding diversity scheme with the same power allocation coefficient. We find two interesting phenomenon from these figures. For top figures, in low SNR range, the capacity performance of two schemes is very close, and from a loss to more gain gradually with ![]() increasing. While in high SNR range, coding diversity scheme achieve more gain than receiving diversity. And, the cross points are higher with
increasing. While in high SNR range, coding diversity scheme achieve more gain than receiving diversity. And, the cross points are higher with ![]() increasing. The cross values are 18 dB, 21 dB and 22 dB, respectively. For bottom figures, in low SNR range, the capacity performance of two schemes are very close. While, the capacity performance of receiving diversity is better than coding diversity in high SNR range, and worse than coding diversity in middle SNR range.
increasing. The cross values are 18 dB, 21 dB and 22 dB, respectively. For bottom figures, in low SNR range, the capacity performance of two schemes are very close. While, the capacity performance of receiving diversity is better than coding diversity in high SNR range, and worse than coding diversity in middle SNR range.
6. Conclusions
This paper presents a rate adaptation scheme for DF relay channel by RPC. We consider a classic relay system model of three nodes, where relay node performs on half-duplex mode. And, we propose receiving diversity and coding diversity relay schemes, and their joint decoding methods. We also discuss the performance of receiving
![]() (a) (b) (c)
(a) (b) (c)![]() (d) (e) (f)
(d) (e) (f)
Figure 9. Capacity performance comparison between receiving diversity scheme and coding diversity scheme with different power allocation coefficients. (a) β1 = 0.2, βr = 0.8; (b) β1 = 0.3, βr = 0.7; (c) β1 = 0.4, βr = 0.6; (d) β1 = 0.8, βr = 0.2; (e) β1 = 0.7, βr = 0.3; (f) β1 = 0.6, βr = 0.4.
diversity and coding diversity schemes with different power allocation coefficients. Simulations show that our DF relay schemes can achieve capacity gain with the help of relay node. Given a SNR, power should be allocated to relay node as far as possible under a condition which ensure relay node can decode successfully.
In the future, we will work on the optimization design of distributed random projections codes by degree distribution and EXIT analysis method. Especially, we focus on how to select weight set and construct random projections matrix.
Acknowledgements
The authors would like to thank the editors and anonymous reviewers. This work was supported in part by the National Nature Science Foundation of China (No. 61305052), the NSF of Jiangxi Province of China Youth Program (No. 20142BAB217007), the Science and Technology Plan Funding of Jiangxi Province of China (No. 20151102040042), and the Research Foundations of Education Bureau of Jiangxi Province (No. GJJ151001, No. GJJ151001, No. GJJ150984).