Received 10 March 2016; accepted 24 April 2016; published 27 April 2016

1. Introduction
Quantitative stock selection has become a research hotspot in the field of investment decision. As a challenging work, it has attracted a large number of scholars. Securities market is a high-dimensional and nonlinear complex system with much noise. How to use the quantification method to select stocks with profit potential from a large number of stocks is the core problem of the quantificative stock selection. In terms of data operation of the securities market, random discrete data seem to change over time. But in the long term, the securities market has certain operation rules. Results obtained with the traditional linear-centered financial time series method still lack rules in the high-dimensional nonlinear securities market, and are still random discrete time series. The development of data mining and gradual maturity of artificial intelligence provides a new opportunity to the solving of high-dimensional and nonlinear problem with much noise. These methods oriented by artificial intelligence include text mining, heuristic algorithm, neural network, fuzzy control based on fuzzy mathematics and so on. Artificial neural network represented by the BP neural network makes the most achievements in dealing with the nonlinear time series. At the same time it progresses rapidly. But BP neural network lacks the expert guidance. With too many optional parameters, the convergence is easy to be very fast, leading to local optimization. There may be the problem of over learning and poor generalization ability. Support Vector Machine (SVM) based on the statistical learning theory is widely used to predict complex high-dimensional nonlinear system in recent years, and many achievements have been made. The problem solved by Support Vector Classification (SVC) or Support Vector Regression (SVR) changes low-dimensional nonlinear problem into high-dimensional linear problem, and simplifies the complex problem. But there are two important problems. First, the selection of SVM parameters has no good solution; second, feature selection has big impact on the performance of the model.
2. Literature Review
In the field of financial application research, SVM has become a widely used method. It is mainly used in the stock index and stock prediction. Kim (2005) [1] was the first to use SVM to predict financial time series data. The empirical results were very superior; Huang (2005) [2] used SVM to predict the stock market, and got the overall trend of the stock market according to the data of the stock market. The empirical results were very ideal; Lee (2009) [3] proposed a mixed feature extraction algorithm predicted stock index combining SVM, first screened characteristic of stock index according to the mixed feature extraction algorithm, and then predicted the stock index according to these feature vectors; Chen, et al. (2009) [4] combined genetic algorithm to optimize FSVM, predicted the stock market data with high-dimensional input space with the model obtained by optimization. The combination of fuzzy algorithm and SVM has better effect than the simple SVM prediction.
Not only time series data is predicted. In this paper SVM is used to select stocks. This is very important in the study in the field of investment and has development prospect, but SVM is seldom used to select and build the quantitative model in this field. Although Palaniswami and Fan (2009) tried to use SVM to solve the problem of stock selection, they just only emphasized on classification of the stocks with SVM. Characteristics of stocks selected are not representative and there are few characteristics, which has big impact on the performance of SVM.
When SVM is used to predict the stock market and individual stocks, selection of stock characteristics is an important problem. The effect of selection of stock characteristics directly has a significant influence on the effect of SVM. According to Yang and Honavar (1998) [5] , the selection of characteristics decides the accuracy of a few classification problems, and affects the cost of classification. This paper chooses SVR to select stocks and build the quantitative stock selection model. It is consistent with the essential idea of regression. So the selection of stock characteristics is very important, and has a great influence on the effect of SVM. Li Yunfei (2009) [6] usedprincipal component analysis (PCA) to extract the value characteristics of stocks, and combined with SVM to identify constituent stocks of Shanghai securities composite index at the same time. Researches show that the model PCA-SVM stock selection model proposed by him has good stock selection ability; Yang Zhen and Xu Guoxiang (2011) [7] extracted characteristics for trading data of Shanghai and Shenzhen 300 Index based on PCA, and used genetic algorithm to optimize support vector machine (SVM), which solved the problem of SVM which could not dynamically sought for parameters. The empirical results show that the prediction precision of Shanghai and Shenzhen 300 Index and large scale share is very high; Chien (2012) [8] used the genetic algorithm to extract stock characteristics and optimize parameters of SVR, ranked the stocks according to the predicted stock yield, and obtained relatively accurate stock selection model; Su Zhi, et al. (2013) [8] used financial data and trading data respectively, used kernel principal component analysis to select characteristics for financial data and trading data, considered the results of feature selection as input vectors of SVR optimized with genetic algorithm, and made medium and long-term and short-term predictions respectively.
Feature selection is an important problem in data mining. The feature selection directly affects the effect of the algorithm model. The conventional feature selection methods include stepwise regression analysis (SRA), principal component analysis (PCA), and currently popular kernel principal component analysis (KPCA) and decision tree (DT), etc. However, these methods can only reveal the correlation or relevance between stock characteristics, and cannot measure the effect of stock characteristics on stock yield, so investors cannot clearly judge the important indicators. Based on this, this paper puts forward the random forest algorithm based on combinational algorithm, and judges the impact of characteristic variables on stock yield by adding noise into characteristic variables, so as to measure the effect of each characteristic variable on stock yield. Some scholars have conducted the in-depth study on screening out characteristic variables with random forest algorithm. Robin, et al. (2010) used random forest to screen important variables to solve the dichotomy problem, comprehensively ranked the variables obtained, and obtained excellent empirical results.
This paper has mainly finished the work in three aspects based on the previous literature. First, from the perspective of value investment, the financial index stock selection system with guiding significance was built, rather than random screened financial data; second, RF-QGA-SVR quantitative stock selection model was built, with the random forest algorithm (RF) financial characteristics were screened, with quantum genetic algorithm (QGA) which could optimize more deeply than standard genetic algorithm (GA) penalty factor c, nuclear parameter g and slack variable p of SVR were dynamically sought for. The robustness of the model could be guaranteed. With RF-QGA-SVR model, stocks were selected in A Share.
3. Construction of RF-QGA-SVR Model
3.1. Support Vector Machine
Different from traditional neural network based on empirical risk minimization, SVM is based on VC dimension of statistical learning theory and the principle of structural risk minimization. According to the finite sample information, compromise is sought between the complexity of model and learning ability, in order to get the best generalization ability. Structural risk includes not only empirical risk, but also confidence risk. By calculating the estimation interval, the upper limit of the whole structure risk can be calculated, which can further ensure the accuracy and generalization ability of the model. Vapnik [9] , et al. were the first to propose SVM in 1995. Mainly according to the labeled training data learning, they obtained the separation function, and effectively solved the problem of data classification. From this perspective, SVM is mainly to solve the classification and regression problem with supervision on learning of tutor.
3.1.1.
Support Vector Classification (SVC)
SVM still maintains good robustness and generalization under the complex high-dimensional linear system mainly by converting low-dimensional nonlinear problem into high-dimensional linear problem. The traditional machine learning method tends to local optimization, over learning and other conditions when dealing with problems under the high-dimensional conditions.SVM proposes to deal with the classification problem of the low-dimensional characteristic space, switch the sample vector to high-dimensional characteristic space by kernel function, and maximize the interval of two classification problems. The sample vector on the edge line is support vector. So support vector machine (SVM) is also known as hyperplane problem to obtain the maximum margin.
When it is linearly separable, a set of data points  are given.
are given.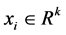 , k is the space dimen-
, k is the space dimen-
sion of input characteristic variable. In which,  is the characteristic input variable,
is the characteristic input variable, 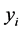 is two category labels, and
is two category labels, and  is maximum separation hyperplane.
is maximum separation hyperplane.
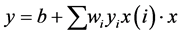 [1] (1)
[1] (1)
In Equation (1) represents dot product, 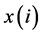 represents the test sample, represents the support vector, and represents offset. The normal vector of the classification hyperplane is obtained by training data of SVM.
represents the test sample, represents the support vector, and represents offset. The normal vector of the classification hyperplane is obtained by training data of SVM.
In order to get the optimal classification hyperplane, the above problem can be converted into convex quadratic programming problem.
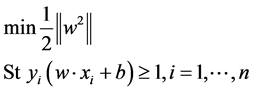 (2)
(2)
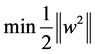 means the object function which guaranteed the maximum gometric interval between the support
means the object function which guaranteed the maximum gometric interval between the support
vectors with different labels. When it is linearly separable, it is converted into high-dimensional version of maximum margin hyperplane.
 (3)
(3)
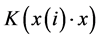 present sernel function. Kernel function is mainly a map used by SVM convert low-dimensional input characteristic variables into high-dimensional input characteristic variables. Common kernel function includes polynomial kernel function
present sernel function. Kernel function is mainly a map used by SVM convert low-dimensional input characteristic variables into high-dimensional input characteristic variables. Common kernel function includes polynomial kernel function  and RBF kernel function. According to the experience of the previous studies, this article selects RBF kernel function as SVR kernel function.
and RBF kernel function. According to the experience of the previous studies, this article selects RBF kernel function as SVR kernel function.
3.1.2.
Support Vector Regression (SVR)
With the deepening of the research problem and expansion of SVM, support vector machine can be used to solve the classification problem. Support vector regression (SVR) is also developed for prediction of regression. The purpose of SVC is to seek for maximum margin classification hyperplane. Different from this, the goal of SVR is mainly to minimize the prediction error, and it is often used in nonlinear regression problem. Many research results have been achieved.SVR has two outstanding characteristics: 1) Based on structural risk minimization principle, regression estimation function is realized, and the generalization ability of the model is ensured. At the same time, insensitive function is used to estimate the structural risk; 2) Empirical risk minimization is combined with empirical error. The non-robust risk function is derived. In this paper, nonlinear function is mainly used.
When the prediction error is minimized, the convex quadratic programming problem is obtained.
 (4)
(4)
 represents the upper limit of the prediction error.
represents the upper limit of the prediction error.
The above model optimization is applicable to most of the training samples with the prediction error, but for some outliers, it will affect the entire model. In order to consider the outliers, the slack variables 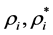 are introduced to build optimization problem.
are introduced to build optimization problem.
![]() (5)
(5)
C represents that the error is beyond the tolerance. The greater C is, the more attention is paid to outliers. ![]() is the insensitive loss function. The introduction of
is the insensitive loss function. The introduction of ![]() improves the estimation robustness. In the empirical study, the researchers need to select and decide C and
improves the estimation robustness. In the empirical study, the researchers need to select and decide C and ![]() by themselves.
by themselves.
By building Lagrange function, the above optimization problem is converted into the dual problem.
![]()
![]()
The most optimal sum ![]() and
and ![]() is obtained.
is obtained.
![]()
![]()
![]()
Similar to SVC, SVR can introduce the kernel function into low-dimensional nonlinear problem, and change into high dimensional-linear problem. The decision function obtained can be turned into:
![]() (6)
(6)
The kernel function selected in this paper is RBF kernel function. Kernel parameter is γ. The selection of γ has important effect on kernel function. If it is set too high, it is easy to cause excessive fitting of the model. On the contrary, it will cause poor learning promotion ability.
3.1.3.
SVR Regression Predicted Value as the Proxy Variable of Stock Yield
In this paper, our purpose is to screen out stocks with profit potential in the future. Through SVR, the precision of stock yield is predicted. It mainly depends on characteristic variables and model parameters. From the perspective of value investment, we look for the preliminary financial indicators from six aspects of A-share listed company, including rationality of earnings per share, profitability, leverage level, liquidity, efficiency level and growth ability.
With SVR the stock yield is predicted. The results obtained are yield agent variables of stock yield. We don’t need perfect prediction results. The main purpose is to rank the stocks by yield from high to low. Assume that F is the input characteristic variable, ![]() is SVR model parameter, and the yield of stock I at time t is
is SVR model parameter, and the yield of stock I at time t is![]() . All the stock yields are predicted, the proxy variable of predicted yield is obtained, and the stocks are ranked. Assume that
. All the stock yields are predicted, the proxy variable of predicted yield is obtained, and the stocks are ranked. Assume that ![]() is the predicted ranking of stock in all the stocks. If
is the predicted ranking of stock in all the stocks. If![]() ,
, ![]() , then:
, then:
![]() (7)
(7)
The goal of this paper is to screen out the top m stocks from all stocks and build a portfolio. The evaluation index of the whole stock portfolio can be built as follows:
![]() (8)
(8)
Here, ![]() represents the ranking of the ith stock at time t,
represents the ranking of the ith stock at time t, ![]() represents the real yield of stock i at time t, and
represents the real yield of stock i at time t, and ![]() represents the average yield of top m stock portfolios at time t. The cumulative yield of m stock portfolios in k years is as follows.
represents the average yield of top m stock portfolios at time t. The cumulative yield of m stock portfolios in k years is as follows.
![]() (9)
(9)
In general, the process steps of the whole algorithm model are as follows:
1) i = 1.
2) Input parameters and the actual yield. Do the model training with SVR.
3) Input the input parameters ![]() of the i + 1th year. Use the SVR model obtained in the ith year to calculate the yield of the i + 1th year of stock to obtain the predicted yield of agent. According to Equation (7), the stocks are ranked.
of the i + 1th year. Use the SVR model obtained in the ith year to calculate the yield of the i + 1th year of stock to obtain the predicted yield of agent. According to Equation (7), the stocks are ranked.
4) m stocks are screened out from results obtained from the previous step. The yield of stocks selected each year is calculated. By Equation (8), the average yield of portfolio m is calculated and obtained.
5) i < −i + 1. Repeat (2)-(4), until i = k − 1.
6) Use Equation (9) to calculate the cumulative yield of corresponding year of top m stocks.
3.2. SVR Model Optimization
SVR model optimization mainly has two aspects. On the one hand, characteristic variable input selection. Important characteristic variables are selected, and the robustness of the model is guaranteed. On the other hand, the model parameter selection has big influence on the performance of the model, so we need to precisely find the parameters and guarantee the prediction ability of the model. In this paper, for SVR parameter optimization, we use the quantum genetic algorithm (QGA) to respectively optimize penalty factor C of SVR, RBF kernel parameter g and slack variable g; with random forest algorithm (RF) SVR input characteristic variables are ranked, and important characteristic variables are screened out, so as to build the RF-QGA-SVR model.
Quantum Genetic Algorithm (QGA)
Quantum genetic algorithm (QGA) is the heuristic global search algorithm developed based on population combining quantum evolutionary algorithm and genetic algorithm with the tenet of “combinatorial optimization”, which give full play to their advantages. As we all know, quantum mechanics play an key role in the physics history, so that the study changes from the deterministic law in the macroscopic world to the quantum motion based on probability theory in the microscopic world, which greatly expands the research category. Because of superposition in the quantum world, the space diversity is ensured. At the same time quantum bit is proposed, and the diversity of information storage is realized. The idea developed combined with genetic algorithm concept based on the population can be deeply searched and analyzed.
Similar to genetic algorithm, the quantum genetic algorithm has consistent idea in terms of the structure from individual to the population, design and calculation of fitness function, and change and update of the individual. The difference is that chromosome in the genetic algorithm only represents a certain chromosome, while chromosome in the quantum genetic algorithm is constructed based on the quantum bit. Quantum chromosome can present the superposition in a number of different states. At the same time, quantum genetic algorithm use squantum rotation gate to update the population and obtain the diversity of population. At the same time the optimal solution of population can be obtained, and the convergence rate of the population can be increased.
In this paper, the principle of SVR cross validation is used to divide training data into 5 tests. The training data is randomly divided into five parts. 4 parts are considered as the training data, and 1 part is considered as the test data. The predicted root mean square error ![]() is considered as the fitness function of quantum genetic algorithm (QGA). The fitness function
is considered as the fitness function of quantum genetic algorithm (QGA). The fitness function ![]() is as follows:
is as follows:
![]() (10)
(10)
This paper uses SVR model parameters optimized by QGA (c, g, p). The algorithm process is as follows:
1) The population size, maximum number of iterations, crossover probability and mutation probability are set.
2) Population initialization.
The initial population consists of N chromosomes. The gene position of each chromosome is represented with quantum bit. The population chromosome is represented as![]() ,. Each chromosome is the binary string with the length of m. There are m observation angles. The kth state representing the binary string
,. Each chromosome is the binary string with the length of m. There are m observation angles. The kth state representing the binary string
![]() is used by
is used by![]() . Assume that the probability amplitude of quantum bit is
. Assume that the probability amplitude of quantum bit is![]() . For the chromo-
. For the chromo-
some with m quantum bits, through the probability amplitude the jth chromosome of the tth generation can be ex-
pressed as ![]()
![]() , all chromosome of the ith generation will have the same
, all chromosome of the ith generation will have the same
form. In which![]() . The sine function and cosine function are used to construct the probability amplitude. The observation angle of initialization quantum bit is
. The sine function and cosine function are used to construct the probability amplitude. The observation angle of initialization quantum bit is![]() , then the probability amplitude is
, then the probability amplitude is![]() . Each chromosome is in all linear superposition with equally likely probability. It can be expressed as:
. Each chromosome is in all linear superposition with equally likely probability. It can be expressed as:
![]() .
.
3) The fitness of each individual in p(t) of the tth generation of population is calculated, and the optimal one ![]() is stored.
is stored.
4) Start to enter the iteration algorithm.
5) Finer operation is conducted on the individual with quantum rotation gate.
Guided by the optimal solution in the current population, the rotation angle is set. Through the observation of the optimal individual and the state of quantum bit corresponding to the current individuals, at the same time with the difference of fitness the direction and size of rotation angle is determined. With the atom as the argument, according to the rotation angle![]() , quantum revolving door can be expressed as:
, quantum revolving door can be expressed as:
![]()
In this paper, the structure of the quantum revolving door strategy is as Table 1.
6) The mutation operation is completed for the quantum non-gate, population individuals are updated, the population diversity is improved, and prematurity and local extremum are avoided.
![]()
7) Through the viewing angle obtained, the corresponding binary solution is generated. In the interval [0, 1] random number r is generated. If![]() , then the corresponding quantum bit collapses to 1. Otherwise it collapses to 0.
, then the corresponding quantum bit collapses to 1. Otherwise it collapses to 0.
8) Continue to calculate the fitness of population and store the optimal value.
9) Determine whether pre-set number of iteration has been reached. If yes, jump out of the algorithm.
3.3. Random Forest (RF)
The traditional classification regression model has many problems. Over fitting and poor generalization ability may appear. In order to solve this problem, many scholars put forward the idea of combination algorithm, used the commonly used classification or regression model as the base classifier, randomly screened out part of data as the training data, got a set of training model of the base classifier, and then summarized according to the predictive results of the base classifier. If the dependent variable is classified variable, weighted voting is required. If the dependent variable is continuous variable, the average shall be taken, and finally the predicted value is decided.
Random forest algorithm uses bootstrap to resample and generate multiple samples with the same number of the samples, and generate the corresponding multiple decision trees. And the difference in the process of generating decision-making tree is that in the selection of characteristic variables of each node not all candidate characteristic variables are selected, but a certain number of characteristic variables are selected in all the characteristic variables, which ensures the diversity of the decision tree. The computing time can be reduced to a certain extent, which guarantees the robustness of the resulting value. The resulting multiple decision trees are voted or averaged according to the value obtained. Study shows that the random forest algorithm can process high- dimensional complex function, be tolerant to abnormality and have strong noise ability. At the same time it will not have excessive fitting. In general, assume that the training set is![]() . Multiple data
. Multiple data
![]()
Table 1. Quantum revolving door strategy.
![]() are sampled and generated by Bagging. By random vector
are sampled and generated by Bagging. By random vector![]() , every decision tree is independently and identically distributed by
, every decision tree is independently and identically distributed by![]() , and eventually a set of
, and eventually a set of ![]() decision tree is generated.
decision tree is generated.
At present, the random forest is mainly used to solve two kinds of problem. The first kind of problem is as follows. According to the existing training data, the learning is supervised, and the important prediction model is built. The second kind of problem is as follows. According to the effect of the characteristic values on the dependent variable, the characteristic values are evaluated and ranked. Characteristic values important for the dependent variable are screened out. The base classifier used by random forest algorithm built in this paper is classification and regression tree (CART). An important feature of the random forest algorithm is out-of-bag data. Random forest uses sampling with replacement. Each decision tree corresponds to data not sampled. These data is called out-of-bag data (OOB). Random forest algorithm can take advantage of these out-of-bag data for internal model validation.
From the six aspects of listed companies, this paper preliminarily screens out 16 financial indexes, and uses random forest to evaluate the importance algorithm of characteristic variable. The structure is as follows:
1) The number of decision-making regression tree random forest (N) is set in advance. At the same time, the number of candidate features of random subspace (m) is set. m < 16. Through the bootstrap algorithm, the sampling with replacement is completed. 200 data is sampled each time, with the same number as the sample size. The decision regression tree is built;
2) The corresponding out-of-bag data (OOB) corresponding to each decision tree is recorded. Without-of-bag data (OOB), the training set is tested, and out-of-bag error is estimated, namely the root mean square error, recorded as MSEOOBerror1; the jth characteristic variable is added into noise, and then out-of-bagerror corresponding to the random forest (MSEOOBerror2) is calculated. The importance of the jth characteristic variable is as follows:
The importance of the jth characteristic variable = ![]()
3) According to the increase of the root mean square error, the importance of impact of candidate financial characteristic variables on stock yield is judged, so as to rank financial characteristic variables, and define the impact of each financial index on stock yield, so as to screen out important financial indicators, which is an important step of RF-QGA-SVR model.
4. Empirical Analysis
4.1. Data Selection and Variable Processing
The top 200 listed companies in terms of market value of a share from 2013 to 2014 are selected (excluding missing data samples). The sample number is 2400. The financial data and annual return are selected as sample. All data comes from wind database and Juyuan database. This paper considers financial characteristics of listed companies as the input variables, and annual return of stock as response variables. Through reading and summary of literature, 16 indexes are screened out from six aspects as the factors of value investment which affect the annual return of stock. Due to the big scope of value range of each index, in order to eliminate the influence of large value and small value, this paper puts financial characteristic variables into the interval [−1.1]. At the same time with Libsvmkit developed by Professor Lin Zhiren of Taiwan University, the empirical results are realized. 16 financial indicators are as shown in the Table 2.
4.2. Empirical Result Analysis
4.2.1.
QGA Parameter Seeking and VS QG Parameter Seeking
To highlight QGA’s parameter seeking ability of SVR transformed in this paper, from 2400 sample data from 2003 to 2014, this paper randomly selects 400 data as the training sample, and 120 data as test samples.QGA is used to optimize SVR’s penalty factor C, nuclear parameter g and slack variable p. The evolution algebra is set as 200, the population is set as 30, the crossover probability is set as 0.7, and the mutation probability is set as 0.1. GA and QGA are operated for 50 times. The results are as in Figure 1 and Figure 2. We use the min ![]() to be best fines sand we calculate the mean of all the population
to be best fines sand we calculate the mean of all the population ![]() at each generation. At the same time, we calculate the mean fitness and best fitness to inspect how the optimization algorithm show at each generation. We want to compare the different optimization algorithm.
at each generation. At the same time, we calculate the mean fitness and best fitness to inspect how the optimization algorithm show at each generation. We want to compare the different optimization algorithm.
Results of QGA and GA optimizing SVR (c, g, p) are shown in the following Table 3.
![]()
Table 2. 16 financial indicators of listed companies.
![]()
Figure 1. GA parameter seeking and iterative evolution process.
From iterative evolution figure of GA and QGA, we can see that the GA convergence speed is too high, values are relatively scattered, and value speed of QGA is relatively homogeneous. It does not tend to local optimal solution. At the same time, goodness of fit ![]() of QGA for test sample is 98.8%, higher than 90.0% of QA. At the same time, the optimal root mean square error
of QGA for test sample is 98.8%, higher than 90.0% of QA. At the same time, the optimal root mean square error ![]() obtained in the process of parameter seeking of QGA is smaller than
obtained in the process of parameter seeking of QGA is smaller than ![]() of GA. From these aspects, it can be seen that optimization of SVR (c, g, p) of QGA proposed in this paper is deeper, and it does not tend to local optimal solution. The generalization
of GA. From these aspects, it can be seen that optimization of SVR (c, g, p) of QGA proposed in this paper is deeper, and it does not tend to local optimal solution. The generalization
![]()
Figure 2. QGA parameter seeking and iterative evolution process.
![]()
Table 3. Comparison of GA and QGA parameter seeking results.
ability is further guaranteed.
4.2.2. SVR Year-to-Year Regression with Full Characteristics of Experience Parameter Belt
Year-to-year regression is completed for data from 2003 to 2014. Stock yields obtained after SVR regression are ranked. The top 10, 20 and 30 stocks in terms of yield are screened out, built and combined, and compared with the benchmark yield of top 200 stocks in terms of market value each year. In order to highlight the change of the investment value, this paper uses Equation (9) to calculate the cumulative yield, and calculates cumulative yield obtained in the corresponding year respectively.
This paper uses Libsvm toolbox to give the empirical parameters. Penalty factor C, nuclear parameter g and slack variable p given according to the experience are (c, g, p) = (10, 0.0625, 0.01), in which 0.0625 is the reciprocal of totally characteristic number. The result of year-to-year regression is as in Figure 3.
In order to highlight changes, the cumulative yield changes calculated with Equation (9) areas in Figure 4.
When experience parameter selecting (c, g, p) = (10, 0.058, 0.01) is selected, with full characteristics, SVR is sued for year-to-year regression prediction of the data from 2004 to 2014. The results obtained are ranked. We can see that top 10, 20 and 30 stocks have to be bought every year and held to the end of the year. In Figure 3, we will find that the annual average yield roughly outperforms the average benchmark yield. From cumulative yield in Figure 4, we can see that the yield of top 10, 20 and 30 stock portfolios is all higher than the benchmark yield. Among them, the investment value of the top 20 stock portfolios reached 35 times from 2003 to 2014. Without parameter optimization and characteristic optimization, the yield of SVR model is higher than benchmark yield.
4.2.3.
SVR Year-to-Year Regression of Experience Parameter of RF Characteristic Optimization Belt
In the previous section, (c, g, p) = (10, 0.0625, 0.01) is used for SVR model without characteristics optimization. In this section, in order to show the impact of characteristic optimization on cumulative yield, the random forest is used to evaluate, rank and screen out important characteristic variables. SVR with characteristic optimization is used for year-to-year regression (in Figure 5 and Figure 6).
![]()
Figure 3. SVR (10, 0.0625, 0.01) annual yield without characteristic optimization.
![]()
Figure 4. SVR (10, 0.0625, 0.01) accumulative yield without characteristic optimization.
![]()
Figure 5. Annual average yield when RF optimizes SVR (10, 0.0625, 0.01).
Based on the empirical parameter (c, g, p) = (10, 0.058, 0.01) of SVR, the random forests (RF) is added for characteristic optimization first. And then RF-SVR after characteristic optimization is used for year-to-year regression and compare with SVR regression without characteristic optimization. Through comparison of Figure 5 and Figure 3, it is found that the annual average yield of SVR after RF optimization is much greater the annual bench mark yield. Among them, the cumulative yield of the top 10, 20 and 30 stocks is higher than the
![]()
Figure 6. Annual cumulative yield when RF optimizes SVR (10, 0.0625, 0.01).
benchmark yield. The investment value of the top 10 stock portfolios reached 235 times from 2003 to 2014. It shows that SVR after RF optimization is more outstanding. The characteristic screening is very necessary.
4.2.4.
SVR Optimized by QGA and SVR without Characteristic Optimization
In order to further compare, this section uses QGA for optimization of SVR and year-to-year regression of QGA-SVR. The empirical results obtained are as in Figure 7 and Figure 8.
The annual average yield of SVR after dynamic parameter seeking of QGA was higher than the benchmark annual average yield from 2004 to 2014. Figure 7 shows SVR after parameter seeking based on empirical parameters. The annual average yield of the top 10, 20 and 30 stock portfolios is higher than the benchmark annual average yield. At the same time, the cumulative yield of the top 10 stocks reached 383 times by 2014,That of the top 20 stocks reached 184 times, and that of the top 30 stocks reached 137 times. This is outperforms than SVR model set according to empirical parameters.
4.2.5. RF-QGA-SVR Model
In this section, year-to-year regression is completed for RF-QGA-SVR model built according to this paper. RF is used to screen out the characteristic variables. QGA optimizes the parameters of SVR (Figure 9 and Figure 10).
From Figure 9 we can see that the average yield obtained by the regression of RF-QGA-SVR model every year of top 10 stock portfolios, top 20 stock portfolios and top 30 stock portfolios is higher than the benchmark annual average yield. At the same time, from Figure 10 and Table 4 we can see that the cumulative yield of the top 10 stock portfolios increased by 1145 times in 2014, that of the top 20 stock portfolios increased by 374 times, and that of the top 30 stock portfolios increased by 264 times. Compared with 17 times of benchmark accumulative yield, it is far higher than the benchmark accumulative earnings.
The portfolio obtained by stock yield ranked by RF-QGA-SVR is more superior to SVR selected according to empirical parameters, belt empirical parameter SVR after RF characteristic optimization and QGA-SVR. At the same time we can see that the yield of the top 10 stock portfolios, top 20 stock portfolios and top 30 stock portfolios obtained by RF-QGA-SVR model gradually increases and presents a certain convergence, which shows to a certain extent it fits the optimal solution ranked by yield.
From 2003 to 2014, in the process of year-to-year regression with RF-QGA-SVR, the use frequency of financial indicators screened out by RF optimization characteristic variables is as in Figure 11.
We use the random forest to calculate the importance of characteristic variables that the importance is above 0.35. The variable that the importance is above 0.35 can guarantee that we get the strong features. From Figure 11, we can see that PB, ROE and ROA are most frequently used financial indicators. They are used in every regression prediction process of RF-QGA-SVR, and belong to the first order of financial gradient, followed by the second order of gradient, including PE, EPS and OPM. The third gradient includes PS, NPM and ITR, so we can see that in the 11 years from 2004 to 2014, A-share market has a large impact on stock yield in three important financial aspects, including the rationality of earnings per share, profitability and efficiency level.
![]()
Figure 7. Annual average yield when QGA optimizes SVR.
![]()
Figure 8. Annual average yield when QGA optimizes SVR.
![]()
Figure 9. Annual average yield of RF-QGA-SVR.
4.2.6. RF-QGA-SVR Model Test
In the above sections, RF-QGA-SVR model uses all the data of each year from 2003 to 2013 as the training data. In fact, the data should be divided into two parts. One part is the training set used to build the model. The other part is the test set used to test the model. The aim is mainly to test whether the model learned on the training set applies to data in the test set.
![]()
Figure 11. Use frequency of financial indicators.
![]()
Table 4. Cumulative yield of RF-QGA-SVR model regression.
To test the model, the data from 2003 to 2014 is divided into two parts. The data of the first n years is considered as the training data, and the data in the rest years (11 − n) is considered as test data. The problem is analyzed from 10 stock portfolios, 20 stock portfolios and 30 stock portfolios.
Tables 5-7 use results from 50 times of iteration of RF-QGA-SVR. We can see that in 11 model validations in the model validation of 10 stock portfolios under the test data the yield of nine times is higher than the benchmark yield. The yield of 10 times of 20 stock portfolios and 30 stock portfoliosis higher than the benchmark yield. At the same time we can see that as the number of stock portfolios selected increases, the standard deviation decreases, and the combined yield becomes more stable. From the above table, we can see that the yields of 30 stock portfolios are more robust.
![]()
Table 5. Model validation of 10 stock portfolios.
![]()
Table 6. Model validation of 20 stock portfolios.
![]()
Table 7. Model validation of 30 stock portfolios.
5. Conclusions
In this paper, RF-QGA-SVR is used as the quantitative stock selection model. With SVR year-to-year regression is completed for A-share stock from 2003 to 2014, and the ranking of stock yield each year is obtained. The top stocks form a portfolio. In order to guarantee the prediction accuracy of SVR, RF is used for characteristic screening of stock characteristic variables. At the same time with QGA penalty factor C, kernel parameter g and slack variable p of SVR are optimized, which ensures the prediction accuracy of SVR to a certain extent.
Through empirical research, we can see that the feature screening of the stocks plays an important role in our proposed model. The effect obtained by stock selection with RF optimization feature is far better than the stocks without characteristic optimization. At the same time, the quantum genetic algorithm (QGA) proposed in this paper carries on deeper optimization of SVR than the traditional genetic algorithm (GA). The effect obtained by stock selection when QGA optimizes SVR is more optimized than SVR selected by experience. At the same time, from the perspective of value investment, we give several important financial indicators with big influence on A-share stock yield, and provide the judgment method for investors.
Overall speaking, the yield of stock portfolios selected by the RF-QGA-SVR model proposed in this paper is much better than the benchmark yield. Therefore, we expect to provide clear idea in terms of quantitative stock selection in the field of quantitative investment. In the future more studies on quantitative stock selection based on SVR model can be provided, and at the same time the selection of financial characteristics affecting the stock yield can be further extended. In terms of the optimization of SVR, we can more diversified group bionic intelligent algorithm, such as evolutionary algorithm (ES) and particle swarm optimization (PSO).