Global Stability in Dynamical Systems with Multiple Feedback Mechanisms ()
Received 16 February 2016; accepted 23 April 2016; published 26 April 2016

1. Outline
First, an n dimensional system with feedbacks from the n’th variable is introduced and some applications from bio-medicine and biochemistry are described. Then, analysis of a scaled version of the system is made including fixed point investigation. Finally, an easy applicable sufficient criterion for a unique, globally stable fixed point is formulated and proved.
Mathematically, the results in this paper follow from the dimensionless form of the equations stated in (6) of Section 2. But before turning to this form we motivate and discuss the dimensional form of the equations in Section 1 as we relate the system to applications and earlier results.
2. Introduction
Many applications of ODEs to physics, chemistry, biology, medicine, and life sciences give rise to non-linear non-negative compartment systems. These include metabolic pathways, membrane transports, pharmacodynamics, epidemiology, ecology, cellular control processes, enzyme synthesis, and control circuits in biochemical pathways [1] - [9] .
This paper concerns the stability of the solutions of such models. More specifically, the paper presents criteria for both local and global stability of all systems of ODEs that can be presented as a compartment model with n compartments, on the form shown in Figure 1. Here the n’th variable may have a non-linear feedback on any of the variables. The main results of this paper are:
・ Existence of a “trapping region”―a compact set with non negative elements in which any solution will be trapped after finite time.
・ At least one fixed point exists and a real valued function of one variable and the system parameters determines the fixed point.
・ A unique, globally stable fixed point exists if the norm of a real valued function of one variable and the system parameters is less than 1.
2.1. Motivating Background
Figure 1 reflects typical hormone regulation. Since a hormone has to bind to a receptor to cause a feedback, a bounded number of receptors justify that the feedback functions 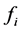 are bounded. Examples of systems corresponding to Figure 1 with
are bounded. Examples of systems corresponding to Figure 1 with 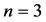 are models of the hypothalamic-pituitary-adrenal axis (HPA axis) concerning the interplay of three hormones in the human body [1] - [5] [10] [11] . Here cortisol exerts a feedback on two other hormones that are involved in the production of cortisol. The system is related to stress and depression. Also testosterone secretion has been modelled by a three dimensional compartment ODE-model including a single feedback [12] which is included in the system investigated here. Similar models exist of gonadotropin hormone secretion [13] , for describing female fertility [14] - [16] and for cellular metabolism [17] .
are models of the hypothalamic-pituitary-adrenal axis (HPA axis) concerning the interplay of three hormones in the human body [1] - [5] [10] [11] . Here cortisol exerts a feedback on two other hormones that are involved in the production of cortisol. The system is related to stress and depression. Also testosterone secretion has been modelled by a three dimensional compartment ODE-model including a single feedback [12] which is included in the system investigated here. Similar models exist of gonadotropin hormone secretion [13] , for describing female fertility [14] - [16] and for cellular metabolism [17] .
A two dimensional model of the HPA axis corresponding to Figure 1 is found in [18] . Here the focus is on a sufficient criterion for a locally stable fixed point. However it is made clear that a global investigation is preferable. Criteria for global stability of solutions are rare. An example is through use of a Liapunov function [6] [12] that can be employed to some problems. Existence and construction of a Liapunov function are unfortunately not easily addressed in general, and Liapunov functions are not used in this article.
Some general and analytical considerations partly similar to our has been considered in previous papers [8] [19] . However, [8] investigate only a feedback from compartment n to compartment 1. The approach of [20] proves the existence of periodic solutions but does not touch upon global stability.
The mathematical results derived in this article relate to the robustness of hormonal systems, cellular metabolism, etc. The existence of a trapping region ensures that non negative initial (hormone) values lead to (hormone) levels that stay non negative and bounded which is reasonable. Existence of locally stable fixed points may be interpreted as states where (hormone) levels may settle. Perturbing parameters such that a solution enters the basin of attraction to another fixed point may then be interpreted as a new (physiological) state (for a person). Or distinct stable fixed points may be interpreted as states for distinct groups (of people). In case of a unique, globally stable fixed point the long term behaviour is very robust to perturbations.
2.2. Mathematical Formulation
We consider an n dimensional system of differential equations with n non negative variables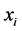 ,
,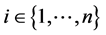 .
. 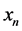 may exert a feedback on all the variables thus making the system non-linear.
may exert a feedback on all the variables thus making the system non-linear.
![]()
Figure 1. Compartment model of the system.
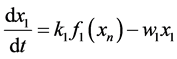 (1a)
(1a)
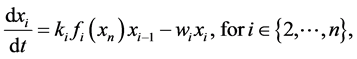 (1b)
(1b)
with production rates 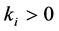 and consumption rates
and consumption rates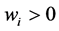 . The feedback from
. The feedback from 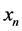 on
on 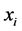 occurs through the function
occurs through the function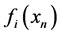 . The following demands are posed for the feedback functions:
. The following demands are posed for the feedback functions: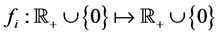 ,
, 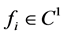 ,
, ![]() and
and![]() ,
, ![]() and
and![]() . The feedbacks are modelled to influence the positive stimulation of the variable in a compartment but with a saturation which justify why the feedbacks must be bounded functions. This means a feedback acts like an adjustable tap that affects the production of variable
. The feedbacks are modelled to influence the positive stimulation of the variable in a compartment but with a saturation which justify why the feedbacks must be bounded functions. This means a feedback acts like an adjustable tap that affects the production of variable ![]() as a function of
as a function of![]() . When modelling many biochemical systems, such as hormone dynamics, saturation is present due to a finite number of binding sites, e.g., receptors. When all binding sites, or receptors, are occupied and work at maximum speed, then an increase in concentration has insignificant effect. The feedback functions must not attain negative values since this corresponds to reverting the flow. When the concentration of
. When modelling many biochemical systems, such as hormone dynamics, saturation is present due to a finite number of binding sites, e.g., receptors. When all binding sites, or receptors, are occupied and work at maximum speed, then an increase in concentration has insignificant effect. The feedback functions must not attain negative values since this corresponds to reverting the flow. When the concentration of ![]() is zero the feedback functions must not cause the production rates to be zero. Therefore,
is zero the feedback functions must not cause the production rates to be zero. Therefore,![]() . In life sciences the consumption rates correspond to elimination rates in general and are therefore by and large constants. However, some results hold even if we allow the wi’s to be bounded non-negative functions of
. In life sciences the consumption rates correspond to elimination rates in general and are therefore by and large constants. However, some results hold even if we allow the wi’s to be bounded non-negative functions of![]() . The models outlined in [1] [3] [10] [18] [12] are covered by Equation (1). An example of a typical feed-
. The models outlined in [1] [3] [10] [18] [12] are covered by Equation (1). An example of a typical feed-
back function is the sigmoidal Hill-function![]() , with
, with![]() ,
, ![]() and
and ![]() being an
being an
integer. Such Hill-functions are often the result of underlying inter cellular enzymatic reactions regulating feedbacks in the quasi-steady-state approximation [21] . In neural networks applications a utilized feedback function is the hyperbolic tangent [22] .
3. Analysis
First a scaling is performed to facilitate the analysis. Defining dimensionless variables ![]() by the equations
by the equations
![]() (2a)
(2a)
![]() (2b)
(2b)
where ![]() and
and ![]() are constants to be defined.
are constants to be defined.
![]() (3)
(3)
Choosing ![]() as a unit of inverse time we get
as a unit of inverse time we get
![]() (4a)
(4a)
![]() (4b)
(4b)
![]() (4c)
(4c)
and
![]() (5)
(5)
A scaling of Equation (1) thus leads to the dimensionless system
![]() (6a)
(6a)
![]() (6b)
(6b)
with constants![]() ,
, ![]() ,
, ![]() and
and ![]() and
and![]() ,
, ![]() and
and![]() .
. ![]() corresponds to a dimensionless time and the value of
corresponds to a dimensionless time and the value of ![]() may be fixed arbitrarily. Differentiation with respect to
may be fixed arbitrarily. Differentiation with respect to ![]() will be noted by a dot such that
will be noted by a dot such that![]() .
.
3.1. Existence and Uniqueness of Solutions
Since ![]() is
is ![]() and locally Lipschitz in
and locally Lipschitz in![]() , for all
, for all ![]() local existence and uniqueness of solutions to Equation (6) are guaranteed given
local existence and uniqueness of solutions to Equation (6) are guaranteed given ![]() . Since the right hand side of Equation (6) in addition fulfils,
. Since the right hand side of Equation (6) in addition fulfils,
![]() (7)
(7)
at least one global solution exists. Here we have made exclusive use of the fact that the![]() ’s are bounded. Combined with the aforementioned local uniqueness result a unique global solution exist. Alternatively one may combine the fact that Equation (6) is autonomous with theorem 3.22 of [23] to guarantee global existence and uniqueness of solutions to Equation (6).
’s are bounded. Combined with the aforementioned local uniqueness result a unique global solution exist. Alternatively one may combine the fact that Equation (6) is autonomous with theorem 3.22 of [23] to guarantee global existence and uniqueness of solutions to Equation (6).
3.2. Positivity of Solutions
Avoiding negative modelling hormone levels is necessary for a sound model and is proved in the following lemma.
Lemma 1. The non negative hypercube is an invariant solution set to Equation (6)
Proof. Given a solution initially in the non negative hypercube we consider the behaviour at a boundary of the hypercube―a hyperplane defined by![]() , for
, for![]() . Considering Equation (6) and first considering
. Considering Equation (6) and first considering ![]()
![]() (8)
(8)
which is non negative for all non negative![]() . Then, considering
. Then, considering ![]()
![]() (9)
(9)
which is a product of non negative factors for all non-negative![]() . This means a solution cannot pass a boundary given by the non negative hypercube due to the aforementioned (local) uniqueness property of solutions. W
. This means a solution cannot pass a boundary given by the non negative hypercube due to the aforementioned (local) uniqueness property of solutions. W
3.3. Existence of a Fixed Point
The fixed point condition of Equation (6) can be expressed
![]() (10)
(10)
This means that for each fixed point value ![]() the fixed point values of the other variables are easily calculated. The equation
the fixed point values of the other variables are easily calculated. The equation
![]() (11)
(11)
may not be explicitly solvable for![]() . However, existence of a solution can be guaranteed and the solution can be numerically approximated.
. However, existence of a solution can be guaranteed and the solution can be numerically approximated.
Define the functions
![]() (12)
(12)
and
![]() (13)
(13)
Thus, finding fixed points of Equation (6) is equivalent to finding ![]() that fulfills
that fulfills![]() . Notice that since
. Notice that since ![]() is bounded we have a bound for R
is bounded we have a bound for R
![]() (14)
(14)
Now choose ![]() for any
for any![]() . Then,
. Then,
![]() (15)
(15)
Furthermore,
![]() (16)
(16)
Define the function ![]()
![]() (17)
(17)
Since L and R are continuous so is ![]() and notice that
and notice that ![]() and
and![]() . Then there exists a
. Then there exists a ![]() such that
such that![]() , i.e.
, i.e.![]() . This means there exists at least one fixed point of the system. Notice that any fixed point is in the set
. This means there exists at least one fixed point of the system. Notice that any fixed point is in the set![]() .
.
3.4. Sufficient Criteria for a Unique Fixed Point
We now discuss a sufficient criterion for existence of a unique fixed point of the system. Let ![]() denote the smallest existing fixed point of Equation (11). If
denote the smallest existing fixed point of Equation (11). If ![]() increase faster than
increase faster than ![]() for all
for all ![]() (this means
(this means ![]() for values of
for values of ![]() larger than
larger than![]() ), there can only be one fixed point. Since
), there can only be one fixed point. Since ![]() a sufficient criteria for only one fixed point is
a sufficient criteria for only one fixed point is![]() ,
, ![]() which is equivalent to
which is equivalent to
![]() (18)
(18)
If the feedback functions correspond to negative feedbacks or are independent of![]() , the criteria is fulfilled since
, the criteria is fulfilled since![]() ,
, ![]() ,
, ![]() Since
Since ![]() only attains non negative values, none positive feedbacks guarantee that there exists exactly one fixed point.
only attains non negative values, none positive feedbacks guarantee that there exists exactly one fixed point.
3.5. Trapping Region
A trapping region is a set, ![]() , where a solution will never escape if it is once in there. It is a physiological desirable property of a model, since this guarantees, that reasonable initial values lead to reasonable levels of the variables for all future time.
, where a solution will never escape if it is once in there. It is a physiological desirable property of a model, since this guarantees, that reasonable initial values lead to reasonable levels of the variables for all future time.
Lemma 2. Let ![]() and define
and define ![]() as
as
![]() (19)
(19)
and define
![]() (20)
(20)
Then ![]() is a trapping region for Equation (6)
is a trapping region for Equation (6)![]() .
.
Proof. ![]() is given. For
is given. For![]() ,
, ![]() for all non negative values of the remaining variables. This means that
for all non negative values of the remaining variables. This means that ![]() is a ‘trapping region’ for
is a ‘trapping region’ for![]() . Using this region for
. Using this region for ![]() we can find a ‘trapping
we can find a ‘trapping
region’ for ![]() and so on by induction. Assume
and so on by induction. Assume![]() . Then for
. Then for ![]() we have
we have
![]() (21)
(21)
This ensures that ![]() is a trapping region. W
is a trapping region. W
Notice that if ![]() then
then ![]() , for
, for![]() ,
,![]() . This means there is a “hierarchy” when finding the trapping region
. This means there is a “hierarchy” when finding the trapping region ![]() has to be bounded before a bound on
has to be bounded before a bound on ![]() can be found.
can be found.
For ![]() then
then![]() . Therefore
. Therefore ![]() is denoted the ‘minimal’ trapping region. Notice that any fixed point of Equation (1) is contained in U.
is denoted the ‘minimal’ trapping region. Notice that any fixed point of Equation (1) is contained in U.
3.6. All Solutions Get Arbitrarily Close to U in Finite Time and Stay Close to U
For any ![]() we can choose
we can choose ![]() such that the distance between elements of
such that the distance between elements of ![]() and U is less than
and U is less than ![]() i.e.
i.e.![]() . We will prove that for any
. We will prove that for any ![]() any solution enters
any solution enters ![]() in finite time (the time depends on the initial condition). Since
in finite time (the time depends on the initial condition). Since ![]() is a trapping region this means that the solution stays less than
is a trapping region this means that the solution stays less than ![]() away from U for all future time.
away from U for all future time.
Lemma 3. Let![]() ,
, ![]() and
and ![]() and
and![]() . If
. If![]() ,
, ![]() then
then![]() ,
,![]() .
.
Proof. Follows by the comparison theorem for integrals. W
Lemma 4. Let![]() ,
, ![]() and
and ![]() and
and![]() . Let
. Let ![]() and let
and let![]() . If
. If![]() ,
, ![]() and
and ![]() is decreasing on
is decreasing on ![]() then there exists
then there exists ![]() such that
such that![]() .
.
Proof. If ![]() then choose
then choose![]() . Else
. Else![]() . Since
. Since ![]() and since f is continuous there exists
and since f is continuous there exists ![]() such that
such that ![]() with
with![]() .
.
Lemma 5. Consider Equation (6). For any ![]() any initial condition leads to a solution in
any initial condition leads to a solution in ![]() after finite time.
after finite time.
Proof. Fix![]() . Assume we have an arbitrary non negative initial condition
. Assume we have an arbitrary non negative initial condition![]() . If
. If ![]() define the compact interval
define the compact interval![]() . Thus
. Thus ![]() on
on![]() .
.
Since ![]() is continuous then
is continuous then ![]() has a maximum
has a maximum ![]() on
on![]() . Using lemma 3 and lemma 4 with
. Using lemma 3 and lemma 4 with
![]() and
and ![]() and
and ![]() there exists a finite time
there exists a finite time ![]() such that
such that![]() . Hence by the proof of theorem 2
. Hence by the proof of theorem 2 ![]() stays in this region for all future time. If
stays in this region for all future time. If ![]() is not yet in
is not yet in ![]() we will have to repeat the argument. In general assume
we will have to repeat the argument. In general assume ![]() for
for![]() . If
. If ![]() then we are done. If
then we are done. If ![]() then form the compact interval
then form the compact interval ![]() as
as
![]() (22)
(22)
Since ![]() is continuous on
is continuous on ![]() a maximum,
a maximum, ![]() , exists and
, exists and ![]() since
since![]() ,
,![]() . Then by lemma 3 and 4 there exists
. Then by lemma 3 and 4 there exists ![]() such that
such that![]() . Then
. Then ![]() is trapped in this set for all future time. This argument ensures there exists
is trapped in this set for all future time. This argument ensures there exists ![]() such that
such that![]() .
.
Since ![]() is a trapping region, a solution once in
is a trapping region, a solution once in ![]() will stay in
will stay in ![]() for all future time. We emphasize that
for all future time. We emphasize that![]() ,
, ![]() may be increasing for some time for some initial conditions outside U.
may be increasing for some time for some initial conditions outside U.
U is the ‘minimal’ trapping region. However, if ![]() is strictly positive on
is strictly positive on ![]() then a smaller trapping region can be found using a lower bound on the derivatives which we will not pursue further here.
then a smaller trapping region can be found using a lower bound on the derivatives which we will not pursue further here.
4. Sufficient Criteria for a Globally Stable Fixed Point
Fix any![]() . Denote
. Denote![]() . Define the function H
. Define the function H
![]() (23)
(23)
![]() (24)
(24)
This means H is the restriction of R to![]() . H only attains non negative values since this is the case for R.
. H only attains non negative values since this is the case for R.
To continue we assume H is positive and a contraction on ![]() which means we assume there exists
which means we assume there exists ![]() such that
such that ![]() and
and ![]() and
and![]() ,
,![]() . This ensures the existence of a unique fixed point of Equation (6). Moreover, any solution of Equation (6) in
. This ensures the existence of a unique fixed point of Equation (6). Moreover, any solution of Equation (6) in ![]() converge to the unique fixed point of the system which will be proven in this section. The approach relies on squeezing the solutions of the Equation (6) with solutions of linear systems. The contraction property then ensures the upper and lower bound converge towards the same limit why the solutions of Equation (6) must converge to that limit, the unique fixed point of Equation (6).
converge to the unique fixed point of the system which will be proven in this section. The approach relies on squeezing the solutions of the Equation (6) with solutions of linear systems. The contraction property then ensures the upper and lower bound converge towards the same limit why the solutions of Equation (6) must converge to that limit, the unique fixed point of Equation (6).
For ![]() define
define
![]() (25a)
(25a)
![]() (25b)
(25b)
Thus, two linear systems of differential equations can be constructed with initial condition ![]() for
for![]() .
.
![]() (26a)
(26a)
![]() (26b)
(26b)
and
![]() (27a)
(27a)
![]() (27b)
(27b)
Then ![]() for
for![]() . Solving the linear systems
. Solving the linear systems
![]() (28)
(28)
![]() (29)
(29)
![]() and
and ![]() are monomiums in
are monomiums in ![]() determined from the initial conditions. If
determined from the initial conditions. If ![]() for
for ![]() then
then ![]() and
and ![]() are constants. With
are constants. With ![]() lemma 3 can be used
lemma 3 can be used
![]() (30)
(30)
Since![]() ,
, ![]() the sums appearing in the solutions of the linear systems get arbitrarily small for increasing time. This means for any
the sums appearing in the solutions of the linear systems get arbitrarily small for increasing time. This means for any ![]() there exists
there exists ![]() such that
such that
![]() (31)
(31)
This means especially
![]() (32)
(32)
Choosing ![]() sufficiently small makes
sufficiently small makes
![]() (33)
(33)
since![]() . The argument may be repeated using the solutions of linear differential equations as bounds for the non-linear system but with a restricted domain for
. The argument may be repeated using the solutions of linear differential equations as bounds for the non-linear system but with a restricted domain for![]() . Define
. Define
![]() (34)
(34)
then![]() ,
,![]() .
.
Define
![]() (35)
(35)
From above there exists a finite time ![]() such that
such that![]() ,
,![]() .
.
Now a sequence of sets, ![]() , is defined
, is defined
![]() (36)
(36)
where
![]() (37)
(37)
and
![]() (38)
(38)
Lemma 6. ![]() in Equation (36) is well defined and compact and
in Equation (36) is well defined and compact and![]() .
.
Proof. The proof is done by induction. ![]() and
and ![]() are given by the expressions
are given by the expressions
![]() (39)
(39)
Since ![]() is compact and H is continuous then
is compact and H is continuous then ![]() and
and ![]() are well defined and finite. This guarantees that
are well defined and finite. This guarantees that ![]() is well defined and compact. Since
is well defined and compact. Since ![]() then
then![]() . Now assume
. Now assume ![]() is well defined and compact. Then
is well defined and compact. Then
![]() (40)
(40)
are well defined and finite. Then ![]() is well defined and compact.
is well defined and compact.
![]() (41)
(41)
Since by assumption![]() , then
, then ![]() and
and![]() . This means
. This means
![]() (42)
(42)
and ensures![]() . W
. W
Due to the squeezing of the solutions using linear systems we have shown that if ![]() then there exists
then there exists ![]() such that
such that ![]() for
for![]() . We may repeat the argument with bounding the solutions of the non-linear differential equations by solutions to linear systems of differential equations. This means there exists
. We may repeat the argument with bounding the solutions of the non-linear differential equations by solutions to linear systems of differential equations. This means there exists ![]() such that if
such that if ![]() then
then ![]() for
for![]() .
.
We now want to prove that ![]() converges to
converges to ![]() meaning that all points of
meaning that all points of ![]() converge to
converge to![]() . The idea of the proof is based on the convergence of
. The idea of the proof is based on the convergence of![]() ,
, ![]() by the Banach Fixed Point Theorem [24] . However, there is also a large number of ‘error terms’ that we have to control. This is done by using the contraction property of H as well as a specific choice of the sequence
by the Banach Fixed Point Theorem [24] . However, there is also a large number of ‘error terms’ that we have to control. This is done by using the contraction property of H as well as a specific choice of the sequence ![]() which is decreasing and positive. Thus, all solutions of the non-linear differential equations converge to the unique fixed point of the system. We need the following two lemmas to prove this main result.
which is decreasing and positive. Thus, all solutions of the non-linear differential equations converge to the unique fixed point of the system. We need the following two lemmas to prove this main result.
Lemma 7. Let p be the contraction constant for H. Then
![]() (43)
(43)
Proof. Follows from the contraction property and the triangle inequality. W
Similarly it follows.
Lemma 8. Let p be the contraction constant for H. Then
![]() (44)
(44)
Lemma 7 and 8 means we can bound the maximum and minimum of H applied on a compact interval by the maximal distance between any two points in the interval and H evaluated at an end point of the interval.
As mentioned a specific choice of ![]() is chosen as a decaying sequence. Introducing a fixed
is chosen as a decaying sequence. Introducing a fixed![]() .
.
![]() (45)
(45)
where ![]() is the contraction constant for H and
is the contraction constant for H and ![]() is given by Equation (34). Choose
is given by Equation (34). Choose ![]() iteratively,
iteratively,
![]() (46)
(46)
For simplicity we put
![]() (47)
(47)
Then,
![]() (48)
(48)
To simplify notation further we introduce
![]() (49)
(49)
Since ![]() then
then
![]() (50)
(50)
Thus,
![]() (51)
(51)
For later use we emphasize that
![]() (52)
(52)
Define
![]() (53)
(53)
![]() and
and ![]() are well defined since repeated use of a continuous function maps compact sets into compact sets.
are well defined since repeated use of a continuous function maps compact sets into compact sets.
![]() and
and ![]() are crucial for the range of
are crucial for the range of![]() . We want to make bounds on
. We want to make bounds on ![]() and
and ![]() using
using ![]() and
and ![]() since we know the latter converges. In
since we know the latter converges. In ![]() “error terms” (
“error terms” (![]() ) are introduced at each step in the sequence. The following lemma helps bounding
) are introduced at each step in the sequence. The following lemma helps bounding ![]() by a series in the ‘error terms’ and a sequence
by a series in the ‘error terms’ and a sequence![]() . This means the “error terms” are separated from
. This means the “error terms” are separated from ![]() and we can then estimate the two separately.
and we can then estimate the two separately.
Lemma 9. If H is a contraction and positive on ![]() then
then
![]() (54)
(54)
Proof. The proof is by induction. Since ![]() and
and ![]() and
and ![]() a basis for the induction is justified. Let
a basis for the induction is justified. Let
![]() (55)
(55)
and
![]() (56)
(56)
We will show
![]() (57)
(57)
By inequality (51)
![]() (58)
(58)
Because ![]() then
then ![]() and
and ![]() since shrinking the domain of a function can only increase the minimum and decrease the maximum of the function values. Thus, from Equation (39)
since shrinking the domain of a function can only increase the minimum and decrease the maximum of the function values. Thus, from Equation (39) ![]() and
and![]() . Using inequality (45) we get from Equation (58)
. Using inequality (45) we get from Equation (58)
![]() (59)
(59)
By equality (34)
![]() (60)
(60)
Using Equation (56)
![]() (61)
(61)
Then,
![]() (62)
(62)
Since H is continuous on the compact sets,
![]() (63)
(63)
Using the contraction property as shown in lemma 7 and lemma 8
![]() (64)
(64)
and
![]() (65)
(65)
From the definitions of ![]()
![]() (66)
(66)
and
![]() (67)
(67)
Thus, we have upper and lower bounds for each of the sets![]() ,
, ![]() ,
, ![]() . From Equations (62)-(67) we get
. From Equations (62)-(67) we get
![]() (68a)
(68a)
![]() (68b)
(68b)
By definition
![]() (69)
(69)
and applying Equation (68)
![]() (70)
(70)
Using Equation (52)
![]() (71)
(71)
which completes the proof. W
Lemma 10. Let H be defined as in Equation (23). If H is a contraction and positive on ![]() then a unique fixed point exists of Equation (6). All solutions in
then a unique fixed point exists of Equation (6). All solutions in ![]() converge to the fixed point.
converge to the fixed point.
Proof. Fix![]() . We will first show that for any
. We will first show that for any ![]() there exists a
there exists a ![]() such that
such that
![]() ,
,![]() . Then the convergence of the remaining
. Then the convergence of the remaining ![]() follows easily.
follows easily.
Since H is a contraction on a complete metric space the Banach Fixed Point Theorem applies, i.e. a uniquefixed point of ![]() for any
for any ![]() exists.
exists.
![]() (72)
(72)
Choose
![]() (73)
(73)
By Equation (72) there exists ![]() such that
such that ![]() for
for![]() ,
,![]() . This means
. This means
![]() (74)
(74)
and similarly
![]() (75)
(75)
There exists a ![]() such that
such that![]() ,
, ![]() ,
,![]() . By lemma 9 and Equation (58)
. By lemma 9 and Equation (58)
![]() (76)
(76)
Inserting from Equations (73)-(76).
![]() (77)
(77)
Therefore ![]() for
for![]() . Hence we have proved that
. Hence we have proved that ![]() converges to
converges to ![]() for any
for any![]() .
.
When ![]() converges to
converges to![]() ,
, ![]() converge to
converge to ![]() since
since ![]() is continuous,
is continuous,![]() . From Equation (28) and Equation (29) this means that
. From Equation (28) and Equation (29) this means that ![]() and
and ![]() converge towards the same limit as
converge towards the same limit as ![]()
![]() (78)
(78)
Since ![]() is squeezed between the limit of
is squeezed between the limit of ![]() and
and![]() .
.
![]() (79)
(79)
This means that all solutions with initial conditions in ![]() converge to the unique fixed point of Equation (6).W
converge to the unique fixed point of Equation (6).W
Since all solutions outside ![]() enter
enter ![]() in finite time then if H is a contraction and positive on
in finite time then if H is a contraction and positive on ![]() all solutions converge to the fixed point as
all solutions converge to the fixed point as ![]() tends to infinity. This implies that no periodic solution exists. Assuming existence of a periodic solution there must be a positive distance between the fixed point and any periodic solution. Since we have just proved that any solution converge to the fixed point then, after some time we have a contradiction which means, there cannot exist any periodic solutions in the trapping region.
tends to infinity. This implies that no periodic solution exists. Assuming existence of a periodic solution there must be a positive distance between the fixed point and any periodic solution. Since we have just proved that any solution converge to the fixed point then, after some time we have a contradiction which means, there cannot exist any periodic solutions in the trapping region.
Sufficient Criteria for a Contraction
A sufficient, easily applicable criteria for H being a contraction can be formulated [24] .
Lemma 11. Let ![]() with
with ![]() compact be
compact be![]() . If
. If![]() ,
, ![]() then f is a contraction.
then f is a contraction.
If H is positive on ![]() and if
and if![]() ,
, ![]() then all solutions of the non-linear system of differential Equation (6) converge to the unique fixed point. However since
then all solutions of the non-linear system of differential Equation (6) converge to the unique fixed point. However since ![]() it is sufficient that
it is sufficient that![]() ,
, ![]() for this conclusion to hold.
for this conclusion to hold.
With the results of Section 3 we now have established the main result of global stability of system (6).
Theorem 1. If![]() ,
, ![]() and
and![]() ,
, ![]() a unique, globally stable fixed point exists of system (6).
a unique, globally stable fixed point exists of system (6).
5. Discussion
The general formulation and results in this paper guarantee that the hormone levels in the models [1] - [7] [10] [20] stay in a trapping region where non-negative concentrations are impossible which is a physiological necessity. A repeating pattern is often visible in hormone levels. However, for Equation (1) periodic solutions are impossible outside the “minimal” trapping region. This narrows the domain for interesting initial conditions. The one dimensional function ![]() contains a lot of relevant information about the system since it determines the fixed point(s) and the derivative gives a sufficient criterion for a globally stable fixed point. In [3] - [5] [7] , the sufficient criteria for a globally stable fixed point are fulfilled for a subset of the physiologically relevant parameter space. In [1] , the focus is on local stability of the fixed point. The investigation of global stability using the criteria found in this paper seems straight forward. Similarly for [18] when the external input to the system is independent of time.
contains a lot of relevant information about the system since it determines the fixed point(s) and the derivative gives a sufficient criterion for a globally stable fixed point. In [3] - [5] [7] , the sufficient criteria for a globally stable fixed point are fulfilled for a subset of the physiologically relevant parameter space. In [1] , the focus is on local stability of the fixed point. The investigation of global stability using the criteria found in this paper seems straight forward. Similarly for [18] when the external input to the system is independent of time.
A model of mRNA and Hes1 protein production fits Figure 1 [25] [26] . However, a time delay in the feedback has to be included in order to obtain experimentally observed oscillations. A model of testorone dynamics including delay in the feedback is investigated in [27] . Including time delays in models corresponding to Figure 1 has proved useful in the search for oscillatory behaviour [28] - [30] . One may wonder whether the feedback itself can cause oscillations or if a time delay needs to be included. The contribution of this paper may help in quickly ruling out oscillatory behaviour in the case of no time delay.
Including time delay in the feedbacks, global stability criteria have been formulated for a subset of possible feedback functions in systems resembling 1 [31] . This requires that all feedbacks are monotone functions. The approach is different from ours and relies on control theory.
Summary
A general formulation of an n-dimensional system of differential equations with up to n feedbacks from the n’th variable is formulated. The feedbacks may be non-linear but must be represented by bounded functions which are considered to be the case for some biological systems. Some relevant general results are shown.
・ Existence and uniqueness of solutions are guaranteed.
・ Non-negative initial conditions cause non-negative solutions for all future time.
・ A trapping region, ![]() , with non-negative elements exists
, with non-negative elements exists![]() . A “minimal” trapping region,
. A “minimal” trapping region, ![]() , exists. The existence of a trapping region is a desirable property if e.g. the system is a model of hormone levels. Then moderate hormone levels are guaranteed for future time if the initial conditions are reasonable.
, exists. The existence of a trapping region is a desirable property if e.g. the system is a model of hormone levels. Then moderate hormone levels are guaranteed for future time if the initial conditions are reasonable.
・ All solutions of the system enter ![]() in finite time for
in finite time for![]() . Then any solution gets arbitrarily close to U in finite time. This eliminates the existence of possible limit cycles outside U.
. Then any solution gets arbitrarily close to U in finite time. This eliminates the existence of possible limit cycles outside U.
・ At least one fixed point exists and all fixed points are contained in U. Using ![]() a sufficient criteria for uniqueness of the fixed point is
a sufficient criteria for uniqueness of the fixed point is
![]() (80)
(80)
If the feedback functions correspond to negative feedbacks or are independent of ![]() then a unique fixed point exists.
then a unique fixed point exists.
・ If![]() ,
, ![]() and
and![]() ,
, ![]() a unique, globally stable fixed point exists.1
a unique, globally stable fixed point exists.1