Optimal Investment and Risk Control Strategy for an Insurer under the Framework of Expected Logarithmic Utility ()
Received 2 March 2016; accepted 23 April 2016; published 26 April 2016

1. Introduction
In the past two decades, more and more attention has been paid to the problem of optimal investment in financial markets for an insurer. Indeed, this is a very important portfolio selection problem for the insurer from a point of finance theory. Merton (1969) [1] first used stochastic control theory to solve consumption and investment problem in framework of continuous financial market. Based on the Merton’s work, Zhou and Yin (2004) [2] , and Sotomayor and Cadenillas (2009) [3] considered consumption/investment problem in a financial market with regime switching. Under the mean-variance criterion and the utility maximization criterion, respectively, they obtained explicit solutions. In view of an external risk which can be insured against by purchasing insurance policy into Merton’s framework, Moore and Young (2006) [4] cooperated and studied optimal consumption, investment and insurance problem. Following Moore and Young (2006) [4] , Perera (2010) [5] resolved the same problem in a more general Levy market. Along the same work, many researchers applied an uncontrollable risk process to Merton’s model, such as Yang and Zhang (2005) [6] . They considered stochastic control problem for optimal investment strategy without consumption under a certain criteria.
For an insurer, since reinsurance is an important tool to manage its risk exposure, optimal reinsurance problem should be considered carefully. This issue implies that the insurer has to select reinsurance payout for certain financial objectives. The classical model for risk in the insurance literatures is Cramer-Lundberg model, which uses a compound Poisson process to measure risk. Based on the limiting process of compound Poisson process, Taksar (2000) [7] wrote the paper about optimal risk and dividend distribution control. Following his same vein, recent researches started to model the risk by diffusion process or a jump-diffusion process; see, e.g. Wang (2007) [8] and Zou (2014) [9] . Considering both proportional reinsurance and step-loss reinsurance, Kaluszka (2001) [10] researched optimal reinsurance in discrete time under the mea-variance criterion. What’s more, recent generalizations in modeling optimal reinsurance process include incorporating regime switching, and interest rate risk and inflation risk; see Zhuo et al. (2013) [11] Guan and Liang (2014) [12] respectively.
In this paper, the model and optimization problem are different from others. Firstly, it is not total wealth of insurer invested, but a part of wealth invested. So in this model, we can obtain the optimal property of the total wealth. Secondly, different from Merton’s work, we use a jump-diffusion process to model an insurer’s risk. Lastly, we regulate the insurer’s risk by controlling the number of polices.
This paper is organized as follow. In Section 2, we formulate investment and risk control problem and describe the financial model and risk process model. The explicit solution of optimal investment and risk control strategy for logarithmic utility is derived in Section 3. In Section 4, we conduct a sensitive analysis. Conclusions of the research are reached in Section 5.
2. The Financial Model and the Risk Process Model
Suppose that there are two assets for investment in the financial market. One is a riskless asset with price process 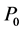 and the other is a risky asset with price process
and the other is a risky asset with price process . The dynamic of
. The dynamic of 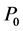 and
and 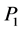 are give by
are give by
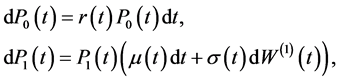 (2.1)
(2.1)
respectively, where 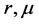 and
and 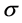 are positive bounded functions and
are positive bounded functions and 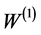 is a standard Brownian motion. The initial conditions are
is a standard Brownian motion. The initial conditions are 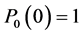 and
and 
For an insurer, most of its incomes come from writing insurance policies, and we denote the total outstanding number of policies at time t by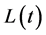 . To simplify our analysis, we assume that the insurer’s average premium for per policy is p, so the total incomes from selling insurance policies over the time period
. To simplify our analysis, we assume that the insurer’s average premium for per policy is p, so the total incomes from selling insurance policies over the time period 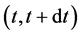 is given by
is given by 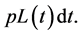
A classical risk model for claims is compound Poisson model, in which the claim for per policy is given by 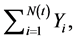 where
where 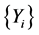 is a series of independent and identically distributed random variables, and
is a series of independent and identically distributed random variables, and ![]() is a Poisson process independent of
is a Poisson process independent of![]() . If the mean of
. If the mean of ![]() and the intensity of
and the intensity of ![]() are finite, such compound Poisson process is a Levy process with finite Levy measure. According to Oksendal and Sulem (2005, Theorem 1.7) [13] , a Levy process can be decomposed into three components, a linear drift part, a Brownian motion part and a pure jump part. Based on this theorem, we suppose the insurer’s risk for per policy is given by
are finite, such compound Poisson process is a Levy process with finite Levy measure. According to Oksendal and Sulem (2005, Theorem 1.7) [13] , a Levy process can be decomposed into three components, a linear drift part, a Brownian motion part and a pure jump part. Based on this theorem, we suppose the insurer’s risk for per policy is given by
![]() (2.2)
(2.2)
where ![]() is a standard Brownian motion and N is a Poisson process defined on the given filtered space, respectively. We assume that
is a standard Brownian motion and N is a Poisson process defined on the given filtered space, respectively. We assume that ![]() are all positive constants. As Stein (2012) [14] considered, we assume
are all positive constants. As Stein (2012) [14] considered, we assume
![]() (2.3)
(2.3)
where ![]() and
and ![]() is another standard Brownian motion, independent of
is another standard Brownian motion, independent of![]() . We also suppose that the Poisson process N has a constant intensity
. We also suppose that the Poisson process N has a constant intensity![]() , and is independent of both
, and is independent of both ![]() and
and![]() .
.
For an insurer, it should be noted that it is impossible for an insurer to invest its total wealth. At time t, we denote ![]() as a part of the insurance wealth invested. Under this consideration, we let
as a part of the insurance wealth invested. Under this consideration, we let ![]() and
and ![]() be the amount invested in the risky asset and the total liabilities respectively. For a strategy
be the amount invested in the risky asset and the total liabilities respectively. For a strategy ![]() the terminal wealth process
the terminal wealth process ![]() is driven by the following SDE:
is driven by the following SDE:
![]() (2.4)
(2.4)
with initial wealth ![]()
Following Stein (2012, chapter 6) [14] , we define the liability radio of liabilities over surplus as ![]()
![]() . We denote
. We denote ![]() as the total proportion of wealth invested,
as the total proportion of wealth invested, ![]() as the proportion of wealth invested in the risky asset at time t. Then for a control
as the proportion of wealth invested in the risky asset at time t. Then for a control![]() , we have
, we have![]() . Then we can rewrite SDE (2.4) as
. Then we can rewrite SDE (2.4) as
![]() (2.5)
(2.5)
with initial wealth![]() .
.
In this model, as Zou (2014) [9] considered, to compensate extra risk by extra return, the coefficients must satisfy the following conditions: ![]() and
and![]() .
.
Define the criterion function as![]() , where
, where ![]() is the terminal time, and
is the terminal time, and ![]() is a
is a
conditional expectation under probability measure P given![]() . The utility function U is assumed to be a strictly increasing and concave. In this paper, the choice for the utility function in economics and finance is
. The utility function U is assumed to be a strictly increasing and concave. In this paper, the choice for the utility function in economics and finance is![]() . We denote
. We denote ![]() as the set of all admissible controls with initial wealth
as the set of all admissible controls with initial wealth![]() . In Section 3, we give the formal definition of
. In Section 3, we give the formal definition of ![]() when
when ![]() and choose either u or
and choose either u or ![]() to be a control. The value function is defined by
to be a control. The value function is defined by
![]() (2.6)
(2.6)
where u will be changed accordingly if the control we choose is![]() .
.
3. The Analysis for ![]()
Firstly formulate the stochastic control problem. The problem in this model is to select an admissible control ![]() (or
(or![]() ) that attains the value function
) that attains the value function![]() . The control
. The control ![]() (or
(or![]() ) is called an optimal control or an optimal policy. We choose u as an admissible control and for every
) is called an optimal control or an optimal policy. We choose u as an admissible control and for every ![]() is progressively measurable and
is progressively measurable and ![]() satisfies the following conditions,
satisfies the following conditions,
![]() . (3.1)
. (3.1)
Furthermore, we assume ![]() while
while ![]() to avoid the possibility of bankruptcy at jumps.
to avoid the possibility of bankruptcy at jumps.
As we know that for![]() , the SDE (2.5) satisfies the linear growth condition and Lipschitz continuity condition, thus by Theorem 1.19 in Oksendal and Sulem (2005) [13] , there exists a unique solution
, the SDE (2.5) satisfies the linear growth condition and Lipschitz continuity condition, thus by Theorem 1.19 in Oksendal and Sulem (2005) [13] , there exists a unique solution ![]() such
such
that ![]() for all
for all ![]()
Applying Ito’s formula to![]() , we can obtain that
, we can obtain that
![]() (3.2)
(3.2)
where ![]() is the compensated Poisson process of N and is a martingale under P. Let
is the compensated Poisson process of N and is a martingale under P. Let
![]() (3.3)
(3.3)
Proposition 3.1. The associated optimal terminal wealth ![]() is strictly positive with probability 1 under optimal control
is strictly positive with probability 1 under optimal control![]() .
.
Proof. According to (2.5) and the Doleans-Dade exponential formula, we have that
![]() (3.4)
(3.4)
From (3.4), to prove ![]() with probability 1, we just need to prove
with probability 1, we just need to prove ![]() with probabili-
with probabili-
ty 1. For any![]() ,
, ![]() and
and ![]() or 0, we have
or 0, we have ![]() So we can obtain that
So we can obtain that
![]() . This implies that
. This implies that ![]() with probability 1.
with probability 1.
Next, we will use the martingale method to get an optimal control for the SDE (2.5). To begin with, we give two important Lemmas. Lemma 3.1 gives the condition that optimal control must satisfy while Lemma 3.2 is a generalized version of martingale representation theorem.
Lemma 3.1. (Wang (2007) [8] ) If there exists a control ![]() such that
such that ![]() is con-
is con-
stant over all admissible controls, then ![]() is optimal control.
is optimal control.
Lemma 3.2. (Wang (2007) [8] ) There exists a predicable process ![]() for any P-martingale Z such that for all
for any P-martingale Z such that for all ![]()
![]() for all
for all![]() . (3.5)
. (3.5)
Now for the value function ![]() we obtain optimal control by 3 steps.
we obtain optimal control by 3 steps.
Step 1: Conjecture candidates for optimal control![]() .
.
Following the definition in Zou (2014) [9] , we also define that
![]() and
and ![]() (3.6)
(3.6)
for any stopping time ![]() almost surely. According to the Proposition 3.1, the process Z is a strictly positive and square-integral martingale under P with
almost surely. According to the Proposition 3.1, the process Z is a strictly positive and square-integral martingale under P with![]() , for all
, for all![]() . Define a new measure Q by
. Define a new measure Q by![]() .
.
From the SDE (2.4), we have
![]() (3.7)
(3.7)
From the above expression of X and Lemma 3.1, for all admissible strategies, we have
![]() (3.8)
(3.8)
is constant.
Define![]() . Since Z is a P-martingale, so is C.
. Since Z is a P-martingale, so is C.
According to Lemma 3.2, there exists a predictable process ![]() such that
such that
![]() (3.9)
(3.9)
From the Doleans-Dade exponential formula, we can obtain that
![]() (3.10)
(3.10)
Through Girsanov’s Theorem, ![]() is a Brownian motion under Q and
is a Brownian motion under Q and
![]() is a martingale under Q.
is a martingale under Q.
For a stopping time ![]() let
let![]() , that is
, that is ![]() and
and![]() ,which is an admissible
,which is an admissible
control. By substituting this control into (3.8), we have ![]() is a constant for all
is a constant for all
![]() which implies that
which implies that ![]() is a Q-martingale.
is a Q-martingale.
So ![]() must satisfy the equation that
must satisfy the equation that
![]() (3.11)
(3.11)
Let ![]() and
and![]() . By a similar way as above, we have
. By a similar way as above, we have
![]() (3.12)
(3.12)
is a Q-martingale, which in turn yields that
![]() (3.13)
(3.13)
From the SDE (2.5), we can derive to![]() ,
,
![]() (3.14)
(3.14)
Comparing the ![]() and
and ![]() terms in (3.10) with (3.14), we obtain that
terms in (3.10) with (3.14), we obtain that
![]() (3.15)
(3.15)
By substituting (3.15) into (3.11) and (3.13), we have that
![]() (3.16)
(3.16)
![]() (3.17)
(3.17)
which the coefficients define as
![]() (3.18)
(3.18)
With the conditions above, solve the Equation (3.17) to get![]() . Since
. Since![]() ,
,
![]() , (3.19)
, (3.19)
where ![]()
According to the (3.19), we can derive ![]() with (3.16).
with (3.16).
Then we choose that ![]() and
and ![]() to get
to get![]() . Similarly, by substituting this control into (3.8), we have
. Similarly, by substituting this control into (3.8), we have
![]() (3.20)
(3.20)
so we can have ![]() by the Equation (3.20).
by the Equation (3.20).
Step 2: Verify that ZT defined by (3.10) is consistent with its definition, for ![]() given in (3.15) and
given in (3.15) and
![]() defined by (3.16), (3.17) and (3.20).
defined by (3.16), (3.17) and (3.20).
First rewrite (3.14) as
![]() (3.21)
(3.21)
where
![]() (3.22)
(3.22)
Then substituting (3.15) back into (3.10), we can obtain ![]() where
where
![]() (3.23)
(3.23)
is constant.
According to the (3.6), Z is a P-martingale and![]() , then
, then![]() . Therefore,
. Therefore,
![]() (3.24)
(3.24)
so Z given by (3.10) with ![]() provided by (3.15) is the same as the definition in (3.6).
provided by (3.15) is the same as the definition in (3.6).
Step 3: Prove that ![]() satisfies the Lemma 3.1.
satisfies the Lemma 3.1.
For any![]() , we give a definition for a new process
, we give a definition for a new process ![]() as follows
as follows
![]() (3.25)
(3.25)
From the Equation (3.13), the above ![]() issue will be 0, and then the process
issue will be 0, and then the process ![]() is a local martingale. As
is a local martingale. As
![]() is a deterministic and bounded, Z is a square-integral martingale under P, that is to say
is a deterministic and bounded, Z is a square-integral martingale under P, that is to say![]() . Meantime, for all
. Meantime, for all![]() , we can obtain that
, we can obtain that![]() , so is
, so is![]() . Therefore, we can derive
. Therefore, we can derive
![]() , (3.26)
, (3.26)
which make possible for us to conclude that the family ![]() is uniformly integral under Q for any stopping time
is uniformly integral under Q for any stopping time![]() . Thus
. Thus ![]() is indeed a martingale under Q with
is indeed a martingale under Q with ![]() for any
for any![]() . So we can prove that Lemma 3.1 is satisfied. Therefore, we have an optimal control for the function
. So we can prove that Lemma 3.1 is satisfied. Therefore, we have an optimal control for the function![]() .
.
4. Sensitive Analysis
In this part, we analyze the influence of the market parameters on the optimal control. To simplify the analysis, we assume that the coefficients are constant in the financial market and the parameters are given in Table 1 which was also used in Zou (2014) [9] . From Table 1, we know that the variables ![]() and
and ![]() are not fixed, so we shall analyze the impact of
are not fixed, so we shall analyze the impact of ![]() and
and ![]() on the optimal control.
on the optimal control.
Firstly, we fix ![]() to research the influence of
to research the influence of![]() . The optimal control of
. The optimal control of ![]() are given by (3.16), (3.17), (3.20), respectively. We draw the graph of optimal control with different values of
are given by (3.16), (3.17), (3.20), respectively. We draw the graph of optimal control with different values of ![]() in Figure 1. From Figure 1, we can know that optimal investment proportion in the securities
in Figure 1. From Figure 1, we can know that optimal investment proportion in the securities ![]() is an increasing function of
is an increasing function of![]() , and the optimal liability ratio
, and the optimal liability ratio ![]() is like a convex function of
is like a convex function of![]() . Besides, the optimal total proportion of wealth invested
. Besides, the optimal total proportion of wealth invested ![]() is decreasing when
is decreasing when ![]() and then increasing. What’s more, the graph shows that
and then increasing. What’s more, the graph shows that![]() . The reason for this behavior comes from the equations of R and
. The reason for this behavior comes from the equations of R and ![]() in (2.2). For our parameters, there is much uncertainty in the insurance market when
in (2.2). For our parameters, there is much uncertainty in the insurance market when ![]() belongs to the interval
belongs to the interval![]() , and hence
, and hence ![]() takes a minimum value in that interval. While
takes a minimum value in that interval. While ![]() takes value near 0 there is little uncertainty, so
takes value near 0 there is little uncertainty, so ![]() takes a maximum value. Since
takes a maximum value. Since ![]() is calculated from the equation (3.16),
is calculated from the equation (3.16), ![]() also takes a maximum value when
also takes a maximum value when ![]() takes value near 0.
takes value near 0.
Secondly, we fix ![]() to analyze the impact of
to analyze the impact of![]() . Consider
. Consider ![]() which include the previous situation
which include the previous situation![]() . We have a graph of optimal control with different value of
. We have a graph of optimal control with different value of ![]() in Figure 2. Figure 2 shows that the optimal investment proportion in the securities
in Figure 2. Figure 2 shows that the optimal investment proportion in the securities ![]() is an increasing function of
is an increasing function of![]() , and the optimal total proportion of wealth invested
, and the optimal total proportion of wealth invested ![]() and the optimal liability ratio
and the optimal liability ratio ![]() are both decreasing function of
are both decreasing function of![]() . This situation is supported by the economic interpretation of
. This situation is supported by the economic interpretation of![]() . In this model, the greater
. In this model, the greater![]() , the more risk for insurers. So, when
, the more risk for insurers. So, when ![]() rises, a risk averse insurer reduces its optimal liability ratio. As the optimal investment expressions (3.17), we know that when
rises, a risk averse insurer reduces its optimal liability ratio. As the optimal investment expressions (3.17), we know that when ![]() raises,
raises, ![]() increases as well. Besides, according to the optimal total proportion of wealth invested
increases as well. Besides, according to the optimal total proportion of wealth invested ![]() and the optimal liability ratio
and the optimal liability ratio ![]() expressions (3.20) and (3.17) respectively, we know that when
expressions (3.20) and (3.17) respectively, we know that when ![]() rises,
rises, ![]() and
and ![]() decreases however.
decreases however.
![]()
Figure 1. Impact of ![]() on the optimal control.
on the optimal control.
![]()
Figure 2. Impact of ![]() on the optimal control.
on the optimal control.
5. Conclusions
In our model, the insurer’s risk process obeys a jump-diffusion process, and it is not total its capital to invest but a part of wealth to invest in financial market. Besides, we consider that an insurer wants to maximize its expected utility of terminal wealth by selecting optimal control. According to the sensitive analysis, we know that the optimal total proportion of wealth invested ![]() and the optimal liability ratio
and the optimal liability ratio ![]() are convex functions of
are convex functions of![]() , but they are both decreasing functions of
, but they are both decreasing functions of![]() . The optimal investment proportion in the securities or derivatives
. The optimal investment proportion in the securities or derivatives ![]() is an increasing function for both
is an increasing function for both ![]() and
and![]() , and
, and![]() . Furthermore, we find that the higher risk insurers get, the lower liability ratio insurers select.
. Furthermore, we find that the higher risk insurers get, the lower liability ratio insurers select.
The limitation in this paper is that the liability is an average for per policy, which conflicts with the fact that the premium for per policy changes all the time for different insurance. Therefore we can research the liability described with a linear function in the model. Besides, the model proposed in the paper can be further explored in another ways as well, something we plan to do in future work.
Acknowledgments
The author thanks to the editor and the reviewers for their thoughtful comments that help the author improve a prior version of this article.