The Analytical Expressions for Computing the Minimum Distance between a Point and a Torus

Xiaowu Li^1*, Linke Hou^2*, Juan Liang^3*, Zhinan Wu⁴, Lin Wang¹, Chunguang Yue^1*

¹College of Information Engineering, Guizhou Minzu University, Guiyang, China.
²Center for Economic Research, Shandong University, Jinan, China.
³Department of Science, Taiyuan Institute of Technology, Taiyuan, China.
⁴School of Mathematics and Computer Science, Yichun University, Yichun, China.

DOI: 10.4236/jcc.2016.44011                

Abstract

In this paper, we present the analytical expressions for computing the minimum distance between a point and a torus, which is called the orthogonal projection point problem. If the test point is on the outside of the torus and the test point is at the center axis of the torus, we present that the orthogonal projection point set is a circle perpendicular to the center axis of the torus; if not, the analytical expression for the orthogonal projection point problem is also given. Furthermore, if the test point is in the inside of the torus, we also give the corresponding analytical expression for orthogonal projection point for two cases.

Keywords

Point Projection, Center Axis of the Torus, Major Planar Circle, Minor Planar Circle, Intersection

Received 2 March 2016; accepted 19 April 2016; published 22 April 2016

1. Introduction

In the various methods mentioned above, all the iterative processes can produce one iterative solution. Different from the above methods, we consider the special situation which the test point have countless corresponding solutions for the orthogonal projection problem. We present the analytical expression for computing the minimum distance between a point and a torus. If the test point is on the outside of the torus and the test point is at the center axis of the the torus, we know that the orthogonal projection point set is a circle which is perpendicular to the center axis of the torus; If not, the analytical expression for the orthogonal projection point problem is also given. In addition, if the test point is in the inside of the torus and is on the major planar circle, then the corresponding analytical expression for orthogonal projection point set is minor planar circle. Moreover, if the test point is in the inside of the torus and is not on the major planar circle, we also present the corresponding analytical expression for orthogonal projection point of the test point.

2. Computing the Minimum Distance between a Point and a Torus

2.1. Test Point Being on the Outside of the Torus

The torus can be defined as

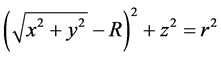(1)

in, where. In this subsection, we suppose that test point 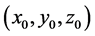is on the outside of the torus, namely,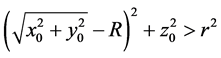. It denotes that the center axis of the torus is the z-axis, the center point is.

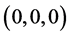Firstly, we deal with the first kind of circumstance which the test point is on the center axis of the torus 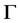, namely the test point’s coordinate is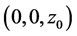. Projecting a test point 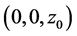onto a torus surface 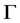can be done as follows. Major planar circle is defined as

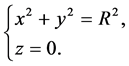(2)

Assume that the coordinates of arbitrary point of major planar circle is 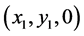which is satisfied

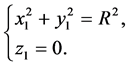(3)

It is not difficult to find that line segment determined by test point and is perpendicular to the torus. So the intersection of line segment and torus is the minimum distance between test point and torus. We can know that parametric equation of the line segment is

(4)

From (1) and (4), we get that the corresponding parameter value of intersection of parametric equation for the line segment and the torus is. Then the intersection of the line segment and the torus is

or another form

(5)

By (3) and (5), we obtain

(6)

In the case of the test point being at the center axis of the torus, Formula (6) indicates that the corresponding orthogonal projection point set of the test point is a circle which parallels to major planar circle (see Figure 1).

In the following content, we try to discuss the second orthogonal projection case which test point is not on the center axis of the torus. This means that neither of the first and second coordinates of the test point are zero. In order to compute the minimum distance between the test point and the torus, we define a plane which passes through the central axis or the z-axis and a line which is determined by the test point and the central point. So the minimum distance between test point and the torus is the intersection between the orthogonal projection line and the torus. In the following, we intend to compute the minimum distance between test point and torus according to this idea. We deduce that the general plane equation passing through the z-axis is

(7)

From (2) and (7), we obtain that the corresponding intersection of the plane and major planar circle of

Figure 1. In the case of the test point being on the center axis of the torus, the corresponding orthogonal projection point set is a circle perpendicular to the center axis of the torus.

the torus is and. If the intersection of the plane and major planar circle of the torus is, then the corresponding vector between this intersection and test point is. Furthermore the parameter equation of the line segment determined by the intersection and test point is

(8)

And because the intersections of the torus and the plane is the following first minor planar circle

(9)

by (8) and (9), the corresponding parameter value of intersection of the line segment and the minor planar circle is. Substituting this parameter value into (8), we obtain the intersection where and . If the intersection of the plane and the major planar circle of the torus is, then the corresponding vector between this intersection and the test point is. Furthermore the parameter equation of the line segment determined by the intersection and the test point is

(10)

Because the intersections of the torus and the plane is the following second minor planar circle

(11)

from (10) and (11), the intersection parameter of the line segment and the second minor planar circle is. Substituting this parameter value into (10), we get the second intersection of the segment line and the torus where

and.

In the following, we explain that the distance between the intersection and the test point is the minimum distance. Because the test point is at the outside of the torus, so. It is easy to know that. From the two inequalities, we get

And because of

so it exists inequality relationship

This demonstrates that the distance between the second intersection and the test point is longer than the distance between the first intersection and the test point. Thus the distance between the intersection and test point is minimum (see Figure 2).

Figure 2. In the case of the test point being not on the center axis of the torus, the corresponding orthogonal projection point of being minimum distance.

Remark 1. If the test point degenerates into the the special point, then the corresponding orthogonal projection point of the special test point would naturally become point. In the same way, if the test point degenerates into the the special point, then the corresponding orthogonal projection point of the special test point would also naturally become point. Of course, if the test point is the special point, then the corresponding orthogonal projection point set of the special test point would be point set presented by Formula (6). In a word, for any test point being on the outside of the torus, we present the corresponding analytical expressions for the orthogonal projection point or the orthogonal projection point set.

2.2. Test Point Being in the Inside of the Torus

In this subsection, we suppose that test point is in the inside of the torus, namely, . Firstly, we deal with the first case which the test point is not on the major circle. In fact, analogous to treatment method of the second part content of the second section, it is easy to verify that orthogonal projection point of the test point is, where

and Now we consider the second case which the test point is in the inside of the torus and is on the major planar circle such that Similar to the treatment method of the first part content of second section, it is easy to know that orthogonal projection point set of the test point is

the corresponding minor planer circle. We directly present the corresponding analytical expression according to the test points being at different positions for major planar circle. Since Formula (9) denotes two minor planer circles, in fact, orthogonal projection point set of arbitrary test point being on the major planar circle just only has one minor planar circle. According to this reason, we try to present a unified and concise analytical expression of the only one minor planar circle for arbitrary test point being on the major planar circle. If, then the corresponding orthogonal projection point set of the test point is minor planer circle

(12)

For more special cases, if test point, then orthogonal projection point set of the test point is the corresponding minor planer circle

(13)

If test point, then the corresponding orthogonal projection point set of the test point is minor planer circle

(14)

If test point, then the corresponding orthogonal projection point set of the test point is minor planer circle

(15)

If test point, then the corresponding orthogonal projection point set of the test point is minor planer circle

(16)

Remark 2. In this subsection, we fully present the corresponding orthogonal projection point or point set of arbitrary test point which is in the inside of the torus, namely, the corresponding analytical expression of orthogonal projection point for the minimum distance between the test point and the torus. If the test point is not on the major planar circle, then the corresponding analytical expression of orthogonal projection point is only one point. If the test point is on the major planar circle, then the corresponding analytical expression of

orthogonal projection point is minor planar circle. Besides that, if the test point satisfies the relationship, it is obviously easy to know that the test point is on the torus.

3. Conclusion

This paper investigates the problem related to a point projection on the torus surface. We present the analytical expression for the orthogonal projection of computing the minimum distance between a point and a torus for all kind s of positions. An area for future research is to develop a method for computing the minimum distance between a point and a general completely center symmetrical surface.

Acknowledgements

We would like to take the opportunity to thank the reviewers for their thoughtful and meaningful comments. This work is supported by the National Natural Science Foundation of China (Grant No. 61263034), the Scientific and Technology Foundation Funded Project of Guizhou Province (Grant No. [2014]2093), the National Bureau of Statistics Foundation Funded Project (Grant No. 2014LY011), the Key Laboratory of Pattern Recognition and Intelligent System of Construction Project of Guizhou Province (Grant No. [2009]4002) and the Information Processing and Pattern Recognition for Graduate Education Innovation Base of Guizhou Province. Linke Hou is supported by the Visiting Scholar Program of the Chinese Scholarship Council (Grant No. 201406225058).

NOTES

^*Corresponding authors.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Ma, Y.L. and Hewitt, W.T. (2003) Point Inversion and Projection for NURBS Curve and Surface: Control Polygon Approach. Computer Aided Geometric Design, 20, 79-99. http://dx.doi.org/10.1016/S0167-8396(03)00021-9
[2]	Yang, H.P., Wang, W.P. and Sun, J.G. (2004) Control Point Adjustment for B-Spline Curve Approximation. Computer- Aided Design, 36, 639-652. http://dx.doi.org/10.1016/S0010-4485(03)00140-4
[3]	Johnson, D.E. and Cohen, E. (1998) A Framework for Efficient Minimum Distance Computations. Proceedings of IEEE International Conference on Robotics & Automation, Leuven, 16-20 May 1998, 3678-3684. http://dx.doi.org/10.1109/robot.1998.681403
[4]	Piegl, L. and Tiller, W. (2001) Parametrization for Surface Fitting in Reverse Engineering. Computer-Aided Design, 33, 593-603. http://dx.doi.org/10.1016/S0010-4485(00)00103-2
[5]	Pegna, J. and Wolter, F.E. (1996) Surface Curve Design by Orthogonal Projection of Space Curves onto Free-Form Surfaces. Journal of Mechanical Design, 118, 45-52. http://dx.doi.org/10.1115/1.2826855
[6]	Besl, P.J. and McKay, N.D. (1992) A Method for Registration of 3-D Shapes. IEEE Transactions on Pattern Analysis and Machine Intelligence, 14, 239-256. http://dx.doi.org/10.1109/34.121791
[7]	Mortenson, M.E. (1985) Geometric Modeling. Wiley, New York.
[8]	Zhou, J.M., Sherbrooke, E.C. and Patrikalakis, N. (1993) Computation of Stationary Points of Distance Functions. Engineering with Computers, 9, 231-246. http://dx.doi.org/10.1007/BF01201903
[9]	Johnson, D.E. and Cohen, E. (2005) Distance Extrema for Spline Models Using Tangent Cones. Proceedings of the 2005 Conference on Graphics Interface, Victoria, May 9-11, 2005, 3 p.
[10]	Hartmann, E. (1999) On the Curvature of Curves and Surfaces Defined by Normalforms. Computer Aided Geometric Design, 16, 355-376. http://dx.doi.org/10.1016/S0167-8396(99)00003-5
[11]	Limaien, A. and Trochu, F. (1995) Geometric Algorithms for the Intersection of Curves and Surfaces. Computers & Graphics, 19, 391-403. http://dx.doi.org/10.1016/0097-8493(95)00009-2
[12]	Polak, E. and Royset, J.O. (2003) Algorithms with Adaptive Smoothing for Finite Minimax Problems. Journal of Optimization: Theory and Applications, 119, 459-484. http://dx.doi.org/10.1023/B:JOTA.0000006685.60019.3e
[13]	Press, W.H., Teukolsky, S.A., Vetterling, W.T. and Flannery, B.P. (1992) Numerical Recipes in C: The Art of Scientific Computing. 2nd Edition, Cambridge University Press, New York.
[14]	Elber, G. and Kim, M.S. (2001) Geometric Constraint Solver Using Multivariate Rational Spline Functions. Proceedings of the Sixth ACM Symposium on Solid Modeling and Applications, 1-10. http://dx.doi.org/10.1145/376957.376958
[15]	Patrikalakis, N. and Maekawa, T. (2001) Shape Interrogation for Computer Aided Design and Manufacturing. Springer Verlag.
[16]	Chen, X.D., Xu, G., Yong, J.H., Wang, G.Z. and Paul, J.C. (2009) Computing the Minimum Distance between a Point and a Clamped B-Spline Surface. Graphical Models, 71, 107-112. http://dx.doi.org/10.1016/j.gmod.2009.01.001
[17]	Selimovic, I. (2006) Improved Algorithms for the Projection of Points on NURBS Curves and Surfaces. Computer Aided Geometric Design, 23, 439-445. http://dx.doi.org/10.1016/j.cagd.2006.01.007
[18]	Cohen, E., Lyche, T. and Riesebfeld, R. (1980) Discrete B-Splines and Subdivision Techniques in Computer-Aided Geometric Design and Computer Graphics. Computer Graphics and Image Processing, 14, 87-111. http://dx.doi.org/10.1016/0146-664X(80)90040-4
[19]	Piegl, L. and Tiller, W. (1995) The NURBS Book. Springer, New York. http://dx.doi.org/10.1007/978-3-642-97385-7
[20]	Chen, X.D., Yong, J.H., Wang, G.Z., Paul, J.C. and Xu, G. (2008) Computing the Minimum Distance between a Point and a NURBS Curve. Computer-Aided Design, 40, 1051-1054. http://dx.doi.org/10.1016/j.cad.2008.06.008
[21]	Liu, X.-M., Yang, L., Yong, J.-H., Guf, H.-J. and Sun, J.-G. (2009) A Torus Patch Approximation Approach for Point Projection on Surfaces. Computer Aided Geometric Design, 26, 593-598. http://dx.doi.org/10.1016/j.cagd.2009.01.004
[22]	Hu, S.M. and Wallner, J. (2005) A Second Order Algorithm for Orthogonal Projection onto Curves and Surfaces. Computer Aided Geometric Design, 22, 251-260. http://dx.doi.org/10.1016/j.cagd.2004.12.001
[23]	Li, X.W., Xin, Q., Wu, Z.N., Zhang, M.S. and Zhang, Q. (2013) A Geometric Strategy for Computing Intersections of Two Spatial Parametric Curves. The Visual Computer, 29, 1151-1158. http://dx.doi.org/10.1007/s00371-012-0758-0