Received 12 March 2016; accepted 18 April 2016; published 21 April 2016

1. Introduction
Rising fishing efforts (and/overexploitation) as well as climate change and their resultant impacts on fisheries stocks are most widely felt by local fisher folks who rely on fishing for their livelihoods. The impacts of these factors on fish stocks (e.g. species abundance, local extinction/disappearance) are discussed elsewhere [1] - [4] . Generally, fluctuations in a country’s annual landings may lead to varying levels of fish imports to augment production shortfalls due to increasing demand. It is therefore imperative that the dynamics of fishery production be understood to allow for efficient management of the local resource base. Hence, estimation of future domestic supply/landings and demand is vital in this regard.
Scientists and policy makers widely rely on predictive models especially, for issues concerning management decisions in relation to fisheries resources. Two different approaches namely deterministic and stochastic models have been developed vis-à-vis forecasting of fisheries landings. Whereas the former is based primarily on the population dynamics theory, stochastic models emanate from the econometric and business literature. Since unobservable variables or unknown lagged processes may be involved in model building procedures, stochastic models are widely employed due to this specific comparative advantage over deterministic models [5] .
Over the past decades, many stochastic models have been developed in both the time (Box-Jenkins and smoothing methods) and frequency (spectral and wavelength analysis) domains. Also, artificial neural networks have been proposed recently and successfully applied to modeling time series data. The applications of time series are diverse including but not limited to disciplines such as ecology [6] - [8] , economics [9] - [11] and medicine [12] [13] among others. In fisheries research however, time series approaches such as artificial neural network and Autoregressive Moving Average models have been used in some studies [14] - [16] . Due to the principal role predictive models play in key management decisions; this work examined the comparative accuracies of different univariate time series approaches in forecasting annual fishery landings.
2. Data and Methods
This study employed yearly data on total fish (TFL) and Sardinella maderensis (SML) landings in Ghana to demonstrate the efficacies of the different time series models used herein. Annual totals of fish production from 1950 to 2013 were obtained from the Food and Agriculture Organization (FAO) fisheries statistics database [17] . However, annual landings of S. maderensis were obtained from the work of [18] . The data constituted a portion of the reconstruction of marine fish catches in Ghana from 1950 to 2010. Each data was subsequently split into a training set (minimum of 50 points) and a test set (10 points). The training set was used to estimate the parameters of the various structural models whereas the test set was used to evaluate their performance.
The ensuing sections briefly describe the theoretical concepts of the techniques employed in the study. Since the data are annual production estimates, only non-seasonal models were considered and elaborated on. All analyses were performed using “R” statistical software [19] .
2.1. Exponential Smoothing Models (ETS)
2.1.1. Naive
Basically, the naïve forecasting approach was employed in order to compare forecasting improvements made by the other methods. This technique always predicts a flat horizontal line in that the best one-step-ahead forecast is the value of the current period. The equation is expressed as:
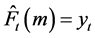 (1)
(1)
2.1.2. Simple Exponential Smoothing (NN)
This technique is best suited for time series data that do not exhibit prevalent trend and seasonality. The general form of the equation is expressed as:
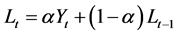 (2a)
(2a)
 (2b)
(2b)
Both the “NN” and Naïve models are equivalent when the value of α = 1.
2.1.3. Holt’s Linear Method (AN)
This two parameter exponential smoothing model was developed to appropriately handle time series exhibiting a prevalent linear trend [20] . The recursive form of the equation is given by:
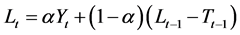 (3a)
(3a)
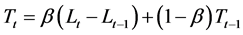 (3b)
(3b)
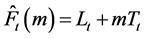 (3c)
(3c)
However, this method is equivalent to Brown’s double exponential smoothing model only if the values of α and β are the same.
2.1.4. Modified Holt’s Method (AdN)
A study by [21] revealed that the “AN” often over estimated trend hence, they introduced a dampening constant (δ) to diminish it. The recursive form of this modified equation is given by:
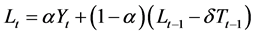 (4a)
(4a)
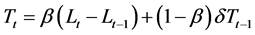 (4b)
(4b)
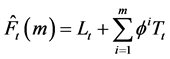 (4c)
(4c)
2.1.5. Pegels’ Method (MN)
Time series that show either a multiplicative or exponential trend are best modeled using Pegels approach [22] . The method is characterized by the equations below:
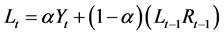 (5a)
(5a)
 (5b)
(5b)
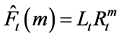 (5c)
(5c)
2.1.6. Modified Pegels’ Method (MdN)
Similar to the “AdN”, the “MN” was modified by adding a dampening parameter (δ) to control exponential growth [23] . The general form of the equation is written as:
 (6a)
(6a)
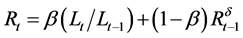 (6b)
(6b)
 (6c)
(6c)
where applicable for each exponential smoothing model, Yt = the time series at the period t; Lt = level, Tt = trend; Rt = growth rate; α = smoothing coefficient for level; β = smoothing coefficient for trend/growth rate; and ![]() = smoothed forecast value for Y.
= smoothed forecast value for Y.
2.2. Autoregressive Integrated Moving Average (ARIMA) Model
This model takes into account past values of the data, prediction errors and a random term [24] . Thus, the Autoregressive (p) portion indicates that the current value of the series can be explained as a function of past values whiles the Moving Average (q) part also shows that the present has a relationship with past shocks. The ARIMA (p, d, q) process is mathematically expressed as:
![]() (7)
(7)
where Yt = the time series at period t; μ = mean of ∆dYt;![]() ;
;![]() ; ϕi and θi denote the ith autoregressive and moving average parameters respectively; d is the differenced order parameter of the process; B and ∆ represent lag and difference operators respectively. In fitting the model, a three-step procedure namely identification, estimation and diagnosis was followed.
; ϕi and θi denote the ith autoregressive and moving average parameters respectively; d is the differenced order parameter of the process; B and ∆ represent lag and difference operators respectively. In fitting the model, a three-step procedure namely identification, estimation and diagnosis was followed.
2.2.1. Unit Root Test
Before building the ARIMA models, a test of stationarity was performed on the fishery landing data using the Kwiatkowski-Phillips-Schmidt-Shin (KPSS) test [25] . The KPSS test is based on the model:
![]() (8)
(8)
![]() ,
,![]() (9)
(9)
where Xt is a random walk with white noise εt. The null hypothesis that Yt is I(0) is simply given as ![]() whiles the alternative is
whiles the alternative is![]() . The test statistic is written as
. The test statistic is written as
![]() (10)
(10)
where ![]() is the number of observations;
is the number of observations;![]() ,
, ![]() is the residual of Yt and;
is the residual of Yt and; ![]() is a consistent estimate of the long-run variance of εt.
is a consistent estimate of the long-run variance of εt.
The null hypothesis of stationarity is rejected if the calculated test statistic is larger than the critical value at a significance level of 5%.
2.3. Artificial Neural Network (ANN) Model
ANNs are simplified models of the biological neural system. The operating principles of this method are fully documented elsewhere [26] . However, in this study, a feed forward network with a single hidden layer was employed due to its general applicability to a variety of different problems [27] . Thus, the Neural Network Autoregression (NNAR) model fitted with lagged values of the series as inputs was used [28] . The general form of the prediction equation [29] for computing forecasts may be written as:
![]() (11)
(11)
where ![]() are the input terms at lags j1, ∙∙∙, jk; {wch} are the weights for the connections between the constant input and the hidden neurons; {wc0} is the weight of the direct connection between the constant input and the output; {wih} and {wh0} respectively represent the weights for other connections between the input and hidden neurons and between the hidden and output neurons; ϕh and ϕ0 respectively symbolize the activation functions that define mappings from inputs to hidden nodes and from hidden nodes to output(s).
are the input terms at lags j1, ∙∙∙, jk; {wch} are the weights for the connections between the constant input and the hidden neurons; {wc0} is the weight of the direct connection between the constant input and the output; {wih} and {wh0} respectively represent the weights for other connections between the input and hidden neurons and between the hidden and output neurons; ϕh and ϕ0 respectively symbolize the activation functions that define mappings from inputs to hidden nodes and from hidden nodes to output(s).
2.4. Model Selection and Diagnostics
Penalized likelihood methods like Akaike’s Information Criterion (AIC), Corrected Akaike’s Information Criterion (AICC) and Bayesian Information Criterion (BIC) were used to select the most appropriate model within groups of competing models. This approach was preferred to measures of forecast error since it penalizes against models with too many parameters. However, due to inconsistent estimators produced by the AIC and AICC, BIC was preferred during model selection.
An overall check of adequacy for the selected models was then conducted using both Ljung-Box and Box- Pierce tests to determine whether residuals are random and independent over time. An ARCH-LM test was also performed on the final models to check for homoscedasticity of model residuals. After selecting and diagnosing the most parsimonious model within each group of competing models, the different structural models were compared using measures of forecast accuracy such as Mean Percent Error (MPE), Mean Absolute Error (MAE), Root Mean Square Error (RMSE), Mean Absolute Percent Error (MAPE) and Mean Absolute Scaled Error (MASE). For each forecast error estimation lower values are preferred. However, much preference was given to MASE during model comparisons since it was proposed to handle deficiencies in both MAPE and scale-depen- dent (RMSE, MAE) error measures [30] .
3. Results
3.1. Model Building and Diagnostics
The various techniques outlined in the previous section have been applied to model annual fishery production data (Figure 1). With regards to the exponential smoothing approach, the selection criteria favored Pegels’ method (α = 0.8140, β = 0.1008) for total fishery landings (TFL). In modeling annual landings of S. maderensis (SML) however, the simple exponential smoothing (α = 0.1216) method was preferred based on information theoretic approaches (Table 1).
In order to fit the ARIMA models, the stationarity of the two series were first investigated. The results of the KPSS test revealed that both total (KPSS = 2.6541, P = 0.01) and S. maderensis (KPSS = 1.6118, P = 0.01) series were not stationary. Hence, each dataset was first differenced to make it stationary such that it fluctuated about the zero point indicating constant mean and variance (TFL − KPSS = 0.0644, P = 0.1; SML − KPSS = 0.0218, P = 0.1; see Figure 2). The rapid decay in the autocorrelation function (ACF) and partial autocorrelation function (PACF) further affirmed the stationarity of the differenced series (TFL and SML) (Figure 3). Various tentative models were then fitted and compared as presented in Table 1 using identified orders of ARIMA (p, 1, q) based on the ACF and PACF plots. For total landings, an ARIMA (0, 1, 0) with drift was chosen since it recorded minimum values for all information criteria values (i.e. drift = 7089.094, SE = 4696.534). However, ARIMA (0, 1, 1) with drift was suitable for modeling annual S. maderensis landings (i.e. MA1 = −1.000, SE = 0.0541; drift = −0.741, SE = 0.136) based on the selection criteria.
![]()
![]()
Figure 1. Time series plot of fishery landings from Ghanaian waters: top―total production (TFL), bottom―S. maderensis (SML).
![]() (a) (b)
(a) (b)
Figure 2. Time series plot of the differenced series: (a) TFL; (b) SML.
![]()
![]()
Figure 3. Correlogram (ACF and PACF) of differenced series for fishery landings: Top panel―TFL, Bottom panel―SML.
![]()
Table 1. Tentative models employed for forecasting fishery landings.
*Means best model based on selection criterion.
These different model structures were then compared to the automatically estimated NNAR(1) and NNAR(7) feed-forward networks for total and S. maderensis landings respectively. The results presented in Table 2 indicate that all the parsimonious models chosen are adequate in accordance with the Ljung-Box (except only ARIMA for SML) and Box-Pierce tests. The homoscedasticity of model residuals were confirmed by the ARCH-LM test which failed to reject the null hypothesis of ARCH effects for the different structural models (Table 2).
3.2. Model Comparisons
As mentioned in the previous section, it should be noted that the naïve model was employed to compare forecast improvements made by the other methods. Forecast plots of the various models selected compared to the test set revealed that the ARIMA model clearly fitted the trend wrongly for total landings (Figure 4). The forecast accuracies of the various models developed for total fishery production are presented in Table 3. The results again show that the ARIMA model over-fits performing well on the training set and poorly on the test set. With none of the two over fitting the data set, both ANN and naïve models performed well as they recorded low forecast
![]()
Table 2. Diagnostic tests on residuals of various structural models.
![]()
Table 3. Accuracy measures of the different forecasting structural models.
error values compared to the others (i.e. “ETS” and ARIMA). With regards to S. maderensis, the ANN model over-fits performing well on the training set and poorly on the test set for most error metrics (Table 3). An examination of Figure 5 however reveals that the ARIMA model underestimates compared to the others. Here, the exponential smoothing approach was superior to the other methods based on all forecast accuracy measures except MAPE.
In order to reliably select an appropriate model, a cross-validation test was further performed and the results presented in Figure 6 and Figure 7. It is observable that ANNs outperform all other models at every forecast
![]()
Figure 4. Comparison of forecast plot (blue line) generated by various forecasting models to the test set (red line)―TFL.
![]()
Figure 5. Comparison of forecast plot (blue line) generated by various forecasting models to the test set (red line)―SML.
![]()
Figure 6. “Cross-validation” of the different structural models―TFL.
![]()
Figure 7. “Cross-validation” of the different structural models―SML.
horizon for total fishery landings (ETS was second best using MASE). However, the exponential smoothing technique was much more appropriate for modeling S. maderensis landings compared to the others (ANN was second best using MASE). Generally, the ARIMA technique performed poorly for both S. maderensis and total fishery landing forecasts.
4. Discussion
When investigating long term variation in fishery production, it is crucial to consider seasonal patterns of landings. However, such monthly time series data may not always be available in some situations. In spite of this, early recognition of production shortfalls based on available data (i.e. yearly landings) is significantly vital in averting depletion of fisheries stocks amidst threats of climate change and other associated pressures. Thus, in this paper, the main interest is to investigate and evaluate the effectiveness of various time series methods in forecasting annual fishery production.
In principle and practice (i.e. methods and results), the differences in the statistical models employed have been briefly demonstrated in the previous sections. Exponential smoothing methods are widely popular because they are robust and relatively easier to compute and apply. Also, the ability of the ARIMA model to capture historical information through AR and MA processes makes it very attractive to researchers especially after the advent of the Box-Jenkins methodology. One comparative advantage of ANNs over the two other methods used is that it can extract non-linear relationships within time series data. This is important since fishery stocks (i.e. abundance, distribution, etc.) may be affected by several factors such as anthropogenic and or climatic variables among others. This major advantage may have accounted for the good performance of ANNs on most forecast error metrics for total fishery landings (e.g. MASE, MAE, MAPE). The findings of this study (both TFL and SML) are also corroborated by other researches which revealed that ARIMA models perform poorly compared to ANNs [31] [32] .
However, it is necessary that the limitations encountered be acknowledged. Firstly, this comparative study only applied three different forecasting techniques among the numerous approaches that exist in literature. For instance, Generalized Autoregressive Conditional Heteroscedasticity (GARCH) models have been proposed to handle various deficiencies in the ARIMA. Also, the feed forward neural network and more specifically the neural network autoregression model is one of several types of artificial intelligence approaches that can be used in time series analysis. However, these three forecasting approaches are employed herein because they are the most typically used by researchers.
As indicated by [33] and confirmed herein (i.e. exponential smoothing vs. ARIMA or ANN―e.g. SML), complex methods do not necessarily yield better forecast accuracies than simple ones. Also, though diagnostic tests revealed that all developed models were adequate, they produced varying forecast results. For instance, while the ARIMA model wrongly predicted the trend in fishery landings (e.g. increased TFL), the other approaches predicted otherwise. Thus, fishery resources will be impacted negatively (i.e. lead to overexploitation) if the ARIMA TFL model which forecasted a false steep rise in landings is considered in the management of the resource. This will in the long run have consequent effects on livelihoods and the economy as a whole. Hence, for efficient making and implementation of management decisions, it is vital that researchers and policy makers examine various time series approaches before applying an appropriate one to time series data.
5. Conclusion
Conclusively, research efforts on predicting fishery landings should be taxonomical (e.g. family, species, etc.) and/or resource specific (e.g. inland; marine―pelagic/demersal) in order to specifically target and ensure efficient management of the fisheries resource base to avoid overexploitation (and its resultant effects on fishery stocks).